Asteraceae
Raymond L. Tremblay
2/24/2022
Activar el paquete principal para las funciones.
library(tidyverse)Añadir los datos en un tibble
Data_L_hoja=tribble(
~Ind, ~Num_Infl, ~L_hoja_cm,
1, 44, 7.3,
2, 93, 6.5,
3, 15, 3.5,
4, 10, 2.6,
5, 9, 1.8
)
Data_L_hoja## # A tibble: 5 × 3
## Ind Num_Infl L_hoja_cm
## <dbl> <dbl> <dbl>
## 1 1 44 7.3
## 2 2 93 6.5
## 3 3 15 3.5
## 4 4 10 2.6
## 5 5 9 1.8Calcular la adecuación relativa
\[w_i=\frac{W_i}{\overline{w}}\]
La adecuación relativa es calculado como la adecuación aboluta de un individuo dividido por el promedio de todo los individuos
w_i=Data_L_hoja$Num_Infl/mean(Data_L_hoja$Num_Infl)
w_i## [1] 1.2865497 2.7192982 0.4385965 0.2923977 0.2631579Ahora poner esta información a la hoja de datos
Data_L_hoja=Data_L_hoja %>%
mutate(w_i=Data_L_hoja$Num_Infl/mean(Data_L_hoja$Num_Infl))Producir un gráfico de la relación entre la adecuación relativa y la variable morfologica, usando puntos para cada planta y construir un modelo lineal con lm.
ggplot(Data_L_hoja, aes(L_hoja_cm, w_i ))+
geom_point()+
geom_smooth(method=lm)## `geom_smooth()` using formula 'y ~ x'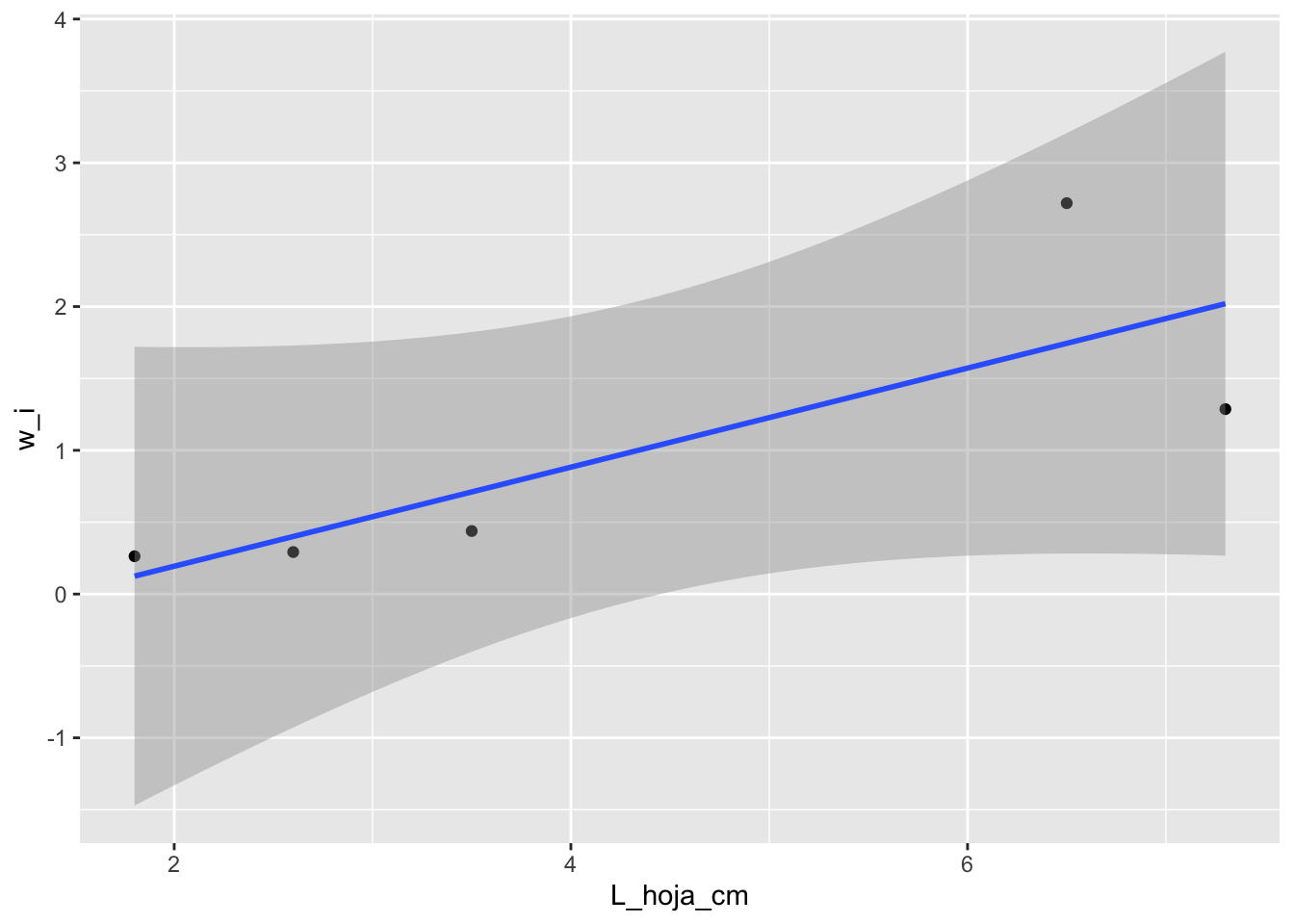
Probando el Modelo lineal si es significativo:
- para determinar si la pendiente es significativa se usa la función lm(y~x, data=los_datos).
El modelo que estamos probando es el siguiente
\[y=beta*x+alpha\]
o
\[y=m*x+b\]
Donde la m y la beta es la pendiente y el alpha y la b es el intercepto.
Resultado de la prueba:
Coefficients: Estimate Std. Error t value Pr(>|t|) (Intercept) -0.4955 0.7279 -0.681 0.545 L_hoja_cm 0.3446 0.1500 2.298 0.105
El intercepto
La primera linea es determrinar si el intercepto es significativamente diferente de cero. En nuestro caso esta parte irrelevante para nosotros. La hipotesis es que b=0, \(H_0: b=0\)
Coefficients: Estimate Std. Error t value Pr(>|t|) (Intercept) -0.4955 0.7279 -0.681 0.545
La pendiente
La hipotersis nula es que la pendiente m es cero, \(H_0: m=0\)
Coefficients: Estimate Std. Error t value Pr(>|t|) L_hoja_cm 0.3446 0.1500 2.298 0.105
Si el valor de P es menor de 0.05 \(p<0.05\), la hipotesis nula se rechaza es se detemrina que hay un patrón significativo.
#Data_L_hoja
model1=lm(w_i~L_hoja_cm, data=Data_L_hoja)
summary(model1)##
## Call:
## lm(formula = w_i ~ L_hoja_cm, data = Data_L_hoja)
##
## Residuals:
## 1 2 3 4 5
## -0.7334 0.9750 -0.2720 -0.1080 0.1384
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) -0.4955 0.7279 -0.681 0.545
## L_hoja_cm 0.3446 0.1500 2.298 0.105
##
## Residual standard error: 0.7288 on 3 degrees of freedom
## Multiple R-squared: 0.6376, Adjusted R-squared: 0.5168
## F-statistic: 5.279 on 1 and 3 DF, p-value: 0.1052