Comp_Intra_Esp_Asteraceae
RLT
3/11/2022
Se encontrará los datos de todos los grupos en el siguiente enlace DATOS
library(readxl)
G5 <- read_excel("G5.xlsx", sheet = "Sheet2")#install.packages("ggplot2", dependencies = TRUE)
library(ggplot2)names(G5)## [1] "Grupo" "Cuadrante" "Num_Plantas"
## [4] "Num_Inflorecencia"ggplot(G5,aes(x=Num_Plantas, fill=Grupo))+
geom_histogram(position="dodge")+
scale_x_continuous(breaks = c(1:9))+
xlab("Números de plantas por cuandrante")+
ylab("Frecuencia")## `stat_bin()` using `bins = 30`. Pick better value with `binwidth`.## Warning: Removed 1 rows containing non-finite values (stat_bin).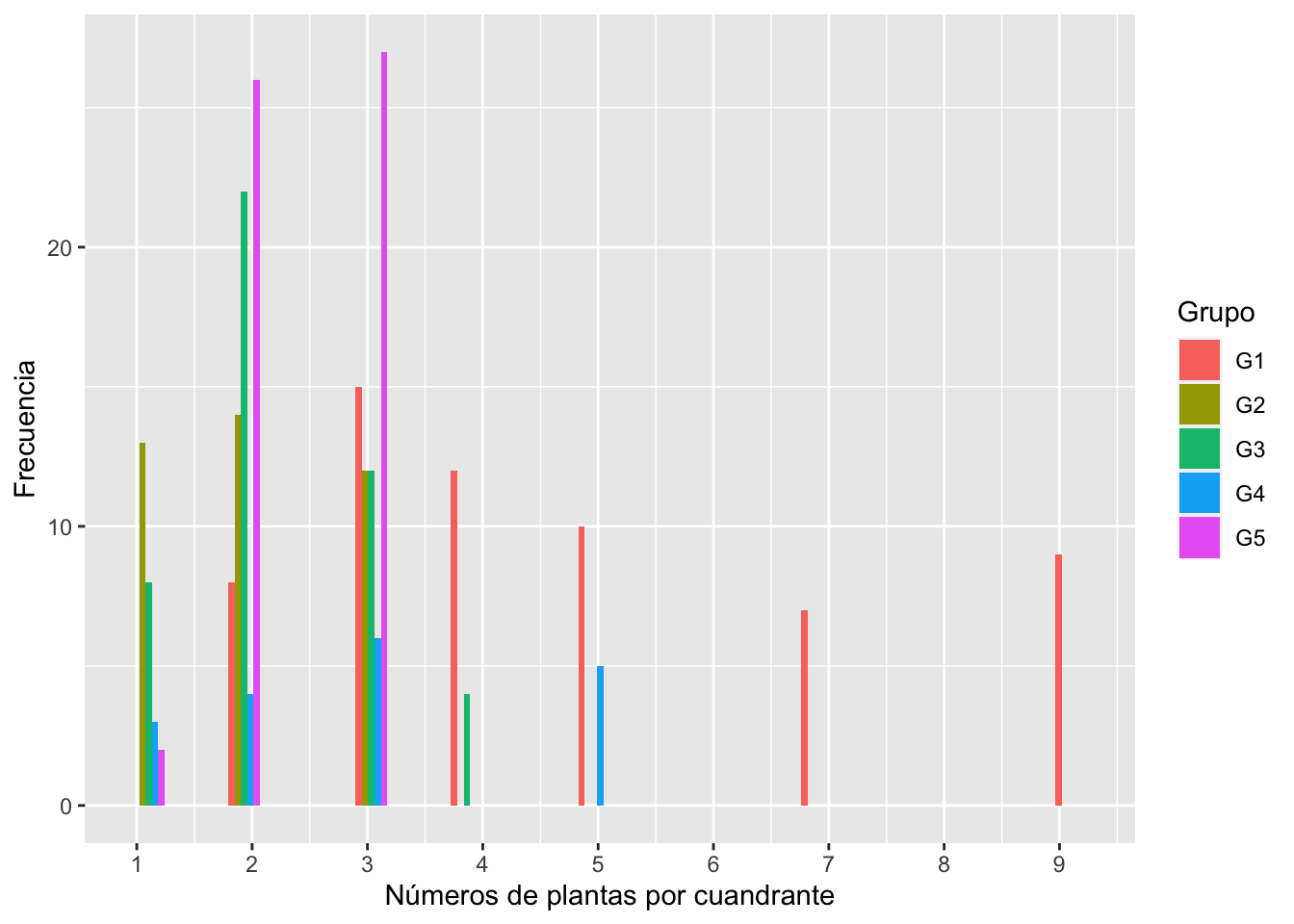
library(ggplot2)
ggplot(G5, aes(Num_Plantas, Num_Inflorecencia, color=Grupo)) +
geom_point()+
geom_smooth(method ="glm", family="poisson")+
facet_wrap(~Grupo)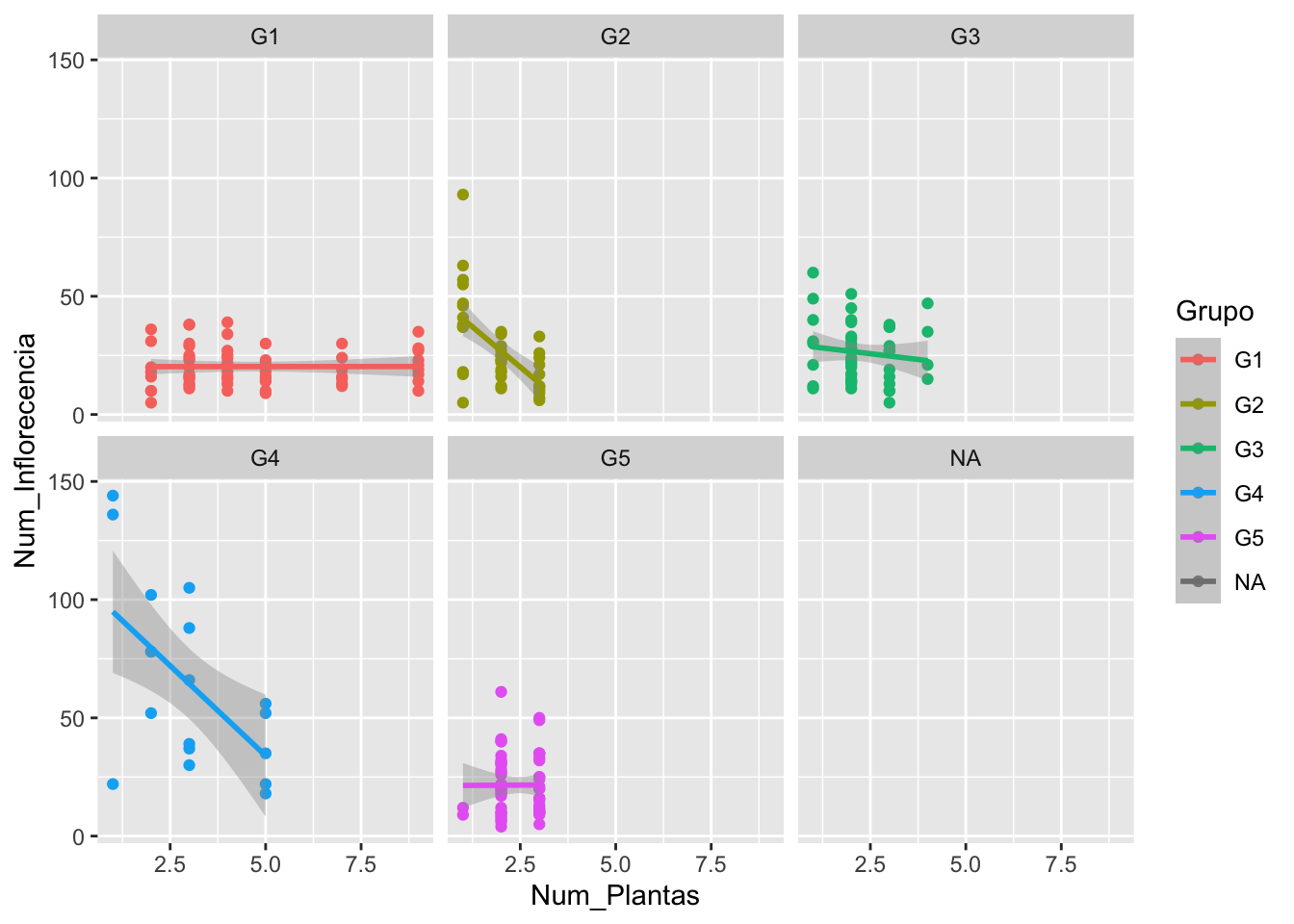
ggsave("Competencia_grupos.png")Model1=glm(Num_Inflorecencia~Num_Plantas+Grupo-1, data=G5 , family="poisson")
summary(Model1) # Estos valores estan en la escala de log_10##
## Call:
## glm(formula = Num_Inflorecencia ~ Num_Plantas + Grupo - 1, family = "poisson",
## data = G5)
##
## Deviance Residuals:
## Min 1Q Median 3Q Max
## -7.4301 -2.3348 -0.2512 1.4740 9.2451
##
## Coefficients:
## Estimate Std. Error z value Pr(>|z|)
## Num_Plantas -0.09494 0.01033 -9.189 <2e-16 ***
## GrupoG1 3.43681 0.05270 65.221 <2e-16 ***
## GrupoG2 3.48797 0.03652 95.516 <2e-16 ***
## GrupoG3 3.47622 0.03667 94.806 <2e-16 ***
## GrupoG4 4.44172 0.04132 107.497 <2e-16 ***
## GrupoG5 3.30259 0.03834 86.128 <2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## (Dispersion parameter for poisson family taken to be 1)
##
## Null deviance: 29660 on 219 degrees of freedom
## Residual deviance: 1570 on 213 degrees of freedom
## (1 observation deleted due to missingness)
## AIC: 2660.7
##
## Number of Fisher Scoring iterations: 5Ahora a ver los coeficiente en la misma escala que se recogio los datos.
exp(coef(Model1))## Num_Plantas GrupoG1 GrupoG2 GrupoG3 GrupoG4 GrupoG5
## 0.9094267 31.0875879 32.7195285 32.3373112 84.9210927 27.1829296Como se interpreta?
Num_Plantas, por cada planta extra en el cuadrante, hay una redución de solamente .6 inflorescencia (1-.94). Por consecuencia en general no se vio mucha diferencia entre la producción de inflorescencia y la cantidad de plantas por cuandrante
Pero los diferentes muestreos (Grupos son distinctos).
Nota que para el primer grupo con una planta se espera 27 inflorescencia y por cada otra planta en el cuandrante se reduce de .6 inflorescencia. Por consecuancia en el primer grupo en un cuadrante de 5 plantas se observa en promedio 27.2 - .937 *5 = 22.5 inflorescencia
El calculo de como calcular la cantidad inflorescencia esperadas en un cuandrate de de 5 plantas en el grupo
27.2 - 0.935*5## [1] 22.525