Variacion_subindividual
Raymond L. Tremblay
3/3/2022
¿Donde se encuentra la variación?
El termino en estadistica se llama “dispersión”
Presentación sobre Variación Subindividual
La presentación siguiente tiene los conceptos principal del concepto de variación subindividual
Trabajo de laboratorio
Evaluar la variación entre individuos y sub-individual de la cantidad de semillas por frutas en una especie de Eucalyptus
Cada estudiante (grupo de 2 solamente) contabilizara 150 frutos, y contará el número de semillas por fruta.
Los datos
- se anade los datos a una hoja de calculo de todos los grupos.
- se evaluará la variación entre individuos y dentro de los individuos.
- Los calculos se harán un grupo
El informe sera guiado por preguntas especificas. (25 puntos)
- Qué es la variación subindividual (comparar con escala de variación)
- Explica los resultados obtenidos abajo en sus propria palabra, ¿que es los que representa estos resultados?
- Menciona 2 ejemplos de la literatura donde se ha estudiado la variación subindividual de la cantidad de semillas y sus resultados (no se le olvida mencionar las referencias)
- En estos 2 ejemplos la variación es más grande entre los individuos o dentro de los individuos
- ¿Por qué se usa el coeficiente de variación y no los datos crudos como el promedio?
- Busca un paper científico sobre otro tema que habal de variación subindividual, y explica en su propria palabra lo que encontraron.
ANALISIS de los datos
library(readxl)
Eucalyptis_2 <- read_excel("Eucalyptis_2.xlsx")
head(Eucalyptis_2)## # A tibble: 6 × 2
## Arbol_Grupo Num_Semillas
## <chr> <dbl>
## 1 A_1 3
## 2 A_1 3
## 3 A_1 3
## 4 A_1 3
## 5 A_1 3
## 6 A_1 4library(tidyverse)Re-organizar los datos en dos columnas
ggplot(Eucalyptis_2, aes(Num_Semillas, fill=Arbol_Grupo))+
geom_histogram()+
facet_wrap(~Arbol_Grupo)## `stat_bin()` using `bins = 30`. Pick better value with `binwidth`.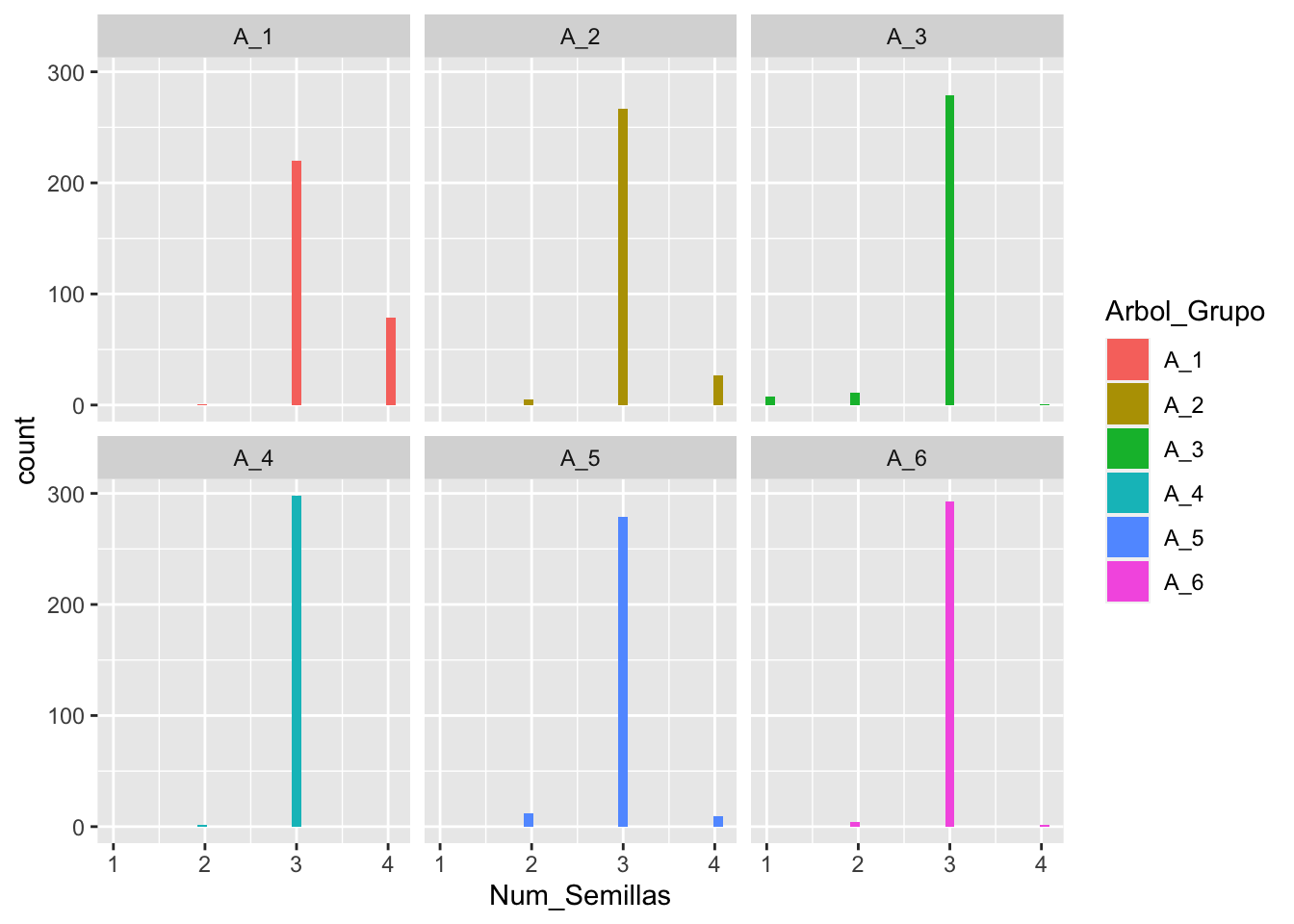
ggsave("Eucalyptis_Histogram.png")## Saving 7 x 5 in image
## `stat_bin()` using `bins = 30`. Pick better value with `binwidth`.Cual es la variación en el número de semillas por árbol
Eucalyptis_2 %>%
select(Num_Semillas, Arbol_Grupo) %>%
group_by(Arbol_Grupo) %>%
drop_na() %>%
summarise(mean= mean(Num_Semillas),
varianza = var(Num_Semillas),
desviación_estandar = sd(Num_Semillas),
CV=desviación_estandar/mean)## # A tibble: 6 × 5
## Arbol_Grupo mean varianza desviación_estandar CV
## <chr> <dbl> <dbl> <dbl> <dbl>
## 1 A_1 3.26 0.200 0.447 0.137
## 2 A_2 3.07 0.102 0.319 0.104
## 3 A_3 2.91 0.140 0.374 0.128
## 4 A_4 2.99 0.00664 0.0815 0.0272
## 5 A_5 2.99 0.0701 0.265 0.0886
## 6 A_6 2.99 0.0201 0.142 0.0474Ahora evaluar si más variación dentro del árbol o entre arboles, usando un analis de varianza (ANOVA)
model1=aov(Num_Semillas~Arbol_Grupo, data = Eucalyptis_2)
summary(model1)## Df Sum Sq Mean Sq F value Pr(>F)
## Arbol_Grupo 5 21.72 4.344 48.38 <2e-16 ***
## Residuals 1791 160.78 0.090
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Nota aqui los resultados de la tabla de ANOVA
El componente de “Sum Sq” = SUm of squares (La suma de los cuadrados)
La parte de Arbol_Grupo representa la variación entre arboles, los residuales, la variación dentro de los grupos.
La diferencia en el promedio entre arboles es distincta
- por que el valor de p es menor de 0.05, nota que tiene “***”
Un gráfico de la variación entre arboles
Hacemos una gráfico de la diferencias entre los arboles y su desviación estandard
E3=Eucalyptis_2 %>%
select(Num_Semillas, Arbol_Grupo) %>%
group_by(Arbol_Grupo) %>%
drop_na() %>%
summarise(mean= mean(Num_Semillas),
varianza = var(Num_Semillas),
desviación_estandar = sd(Num_Semillas),
CV=desviación_estandar/mean)
E3## # A tibble: 6 × 5
## Arbol_Grupo mean varianza desviación_estandar CV
## <chr> <dbl> <dbl> <dbl> <dbl>
## 1 A_1 3.26 0.200 0.447 0.137
## 2 A_2 3.07 0.102 0.319 0.104
## 3 A_3 2.91 0.140 0.374 0.128
## 4 A_4 2.99 0.00664 0.0815 0.0272
## 5 A_5 2.99 0.0701 0.265 0.0886
## 6 A_6 2.99 0.0201 0.142 0.0474ggplot(E3, aes(y=mean, x=Arbol_Grupo))+
geom_point()+
geom_errorbar(aes(ymin=mean-desviación_estandar, ymax=mean+desviación_estandar), width=.2,
position=position_dodge(0.05))+
ylab("Promedio y la desviación estandard \ndel número de semillas por fruto")+
xlab("Arboles muestrados")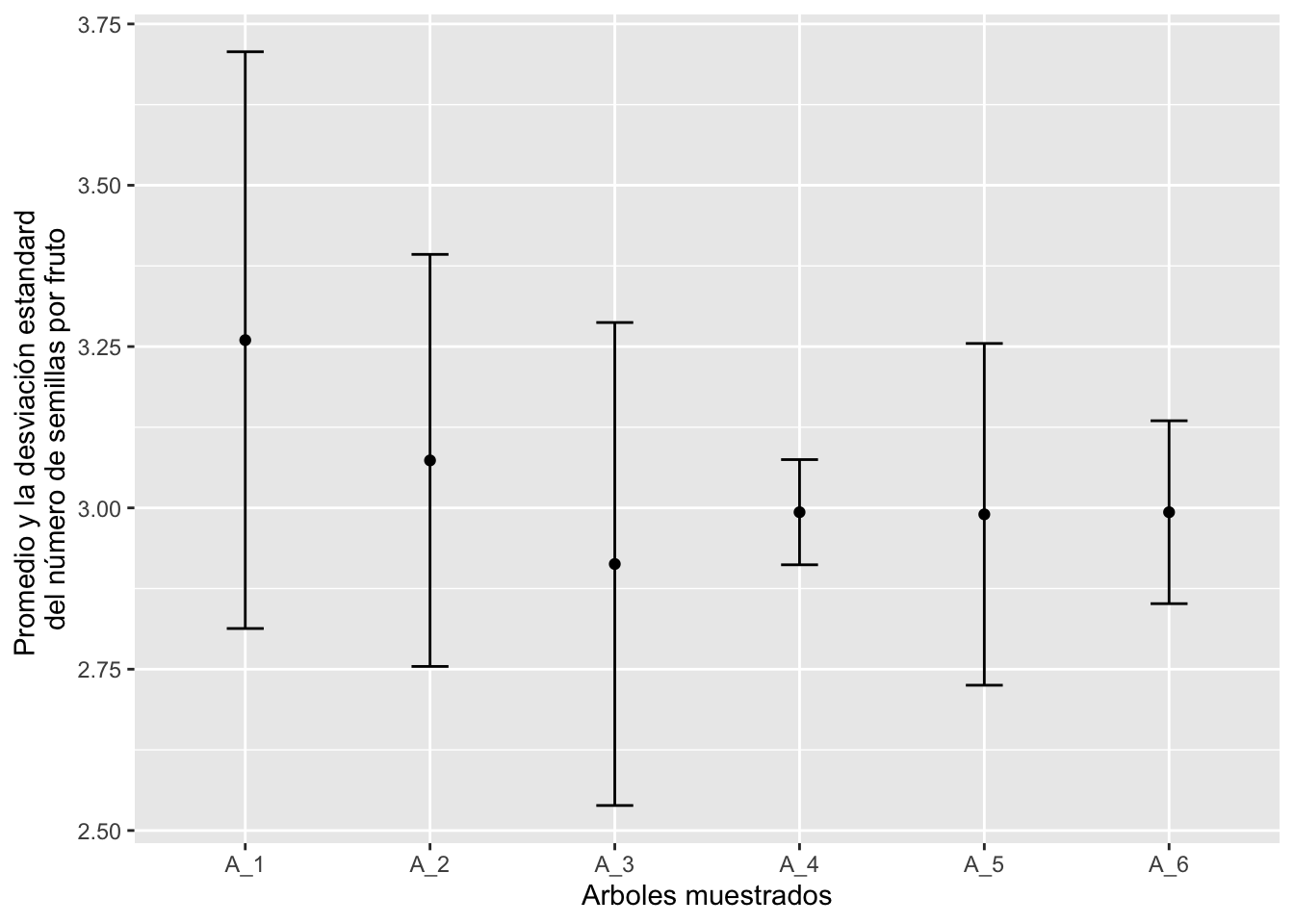
ggsave("mean_SD.png")## Saving 7 x 5 in image