Malthus y el comienzo de Ecología de Poblaciones
BIOL4558
Agosto 2021
Thomas Robert Malthus (1766 – 1834) fue un clérigo inglés que escribió uno de los ensayos más importantes e influyentes jamás escritos: Un ensayo sobre el principio de población 
El punto principal de este ensayo se puede resumir en lo siguiente (una cita directa):
“El poder de la población es indefinidamente mayor que el poder de la tierra para producir la subsistencia del hombre” - El Rev. Thomas Malthus
“The power of population is indefinitely greater than the power in the earth to produce subsistence for man” - The Rev. Thomas Malthus
O en una forma más detallada …
“Creo que puedo hacer dos postulados. Primero, que la comida es necesaria para la existencia del hombre. En segundo lugar, que la pasión entre los sexos es necesaria y permanecerá casi en su estado actual … Asumiendo entonces mi postulado como concedido, el poder de la población es indefinidamente mayor que el poder de la tierra para producir la subsistencia del hombre. La población, cuando no se controla, aumenta en una proporción geométrica. La subsistencia aumenta sólo en una proporción aritmética. Un ligero conocimiento de Los números mostrarán la inmensidad del primer poder en comparación con el segundo. Según la ley de nuestra naturaleza que hace necesario el alimento para la vida del hombre, los efectos de estos dos poderes desiguales deben mantenerse iguales. controlar a la población por la dificultad de subsistencia. Esta dificultad debe caer en alguna parte y debe ser necesariamente sentida por una gran parte de la humanidad …”
“I think I may make fairly two postulata. First, that food is necessary to the existence of man. Secondly, that the passion between the sexes is necessary and will remain nearly in its present state … Assuming then my postulata as granted, I say, that the power of population is indefinitely greater than the power in the earth to produce subsistence for man. Population, when unchecked, increases in a geometrical ratio. Subsistence increases only in an arithmetical ratio. A slight acquaintance with numbers will show the immensity of the first power in comparison of the second. By the law of our nature which makes food necessary to the life of man, the effects of these two unequal powers must be kept equal. This implies a strong and constantly operating check on population from the difficulty of subsistence. This difficulty must fall somewhere and must necessarily be severely felt by a large portion of mankind…”
Finalmente, su argumento económico se puede resumir de la siguiente manera:
- Siempre hay límites estrictos para el crecimiento de la población (humana), y estos límites tienen que ver con la disponibilidad de alimentos,
- Cuando haya más alimentos disponibles, los humanos tenderán a utilizarlos para la reproducción,
- Que solo prevendrá temporalmente una crisis cuando lleguemos inevitablemente a los límites del crecimiento, lo que conducirá a:
- Hambrunas, enfermedades, etc. generalizadas, especialmente entre las poblaciones pobres y desfavorecidas.
¿Es este un mensaje optimista o un mensaje pesimista?
“If they would rather die they had better do it, and decrease the surplus population” - Ebenezer Scrooge
Pregunta de discusión: ¿Malthus tenía razón? ¿Para humanos? ¿Por la vida salvaje? ¿Puedes pensar en algún ejemplo a favor o en contra?

Curiosamente, en 1838 (cuatro años después de la muerte de Malthus), Charles Darwin, que acababa de regresar de su viaje en el HMS Beagle (1831-1836), buscaba posibles mecanismos para explicar el origen de las especies. Al leer el Ensayo sobre el principio de población de Malthus, se dio cuenta de una de las posibles implicaciones de los controles que controlaban el crecimiento de la población (es decir, que el poder del crecimiento exponencial significa que nacerán muchos individuos que no podrán sobrevivir hasta la edad adulta debido a limitaciones de recursos) y escribió:
’… las variaciones favorables tenderían a conservarse y las desfavorables a destruirse … El resultado de esto sería la formación de una nueva especie. Aquí, entonces, por fin tenía una teoría con la que trabajar. - Charles Darwin
‘…favourable variations would tend to be preserved, and unfavourable ones to be destroyed … The result of this would be the formation of a new species. Here, then, I had at last got a theory by which to work.’ - Charles Darwin
Veintiún años después, Darwin publicó su libro * Sobre el origen de las especies mediante la selección natural *. Como el trabajo de Malthus, también generó una tormenta de controversia y protesta.
¿Entonces, qué piensas? El * Ensayo * de Mathus fue extremadamente influyente, ¿verdad?
Ejercicio en clase: límites al crecimiento
Malthus estaba convencido de que el crecimiento de la población humana sobrepasaría el límite, es decir, las poblaciones crecerán hasta que se agoten los alimentos. Cual es el resultado? ¡Hambre, sufrimiento, enfermedad! ¡Modelemos esto!
Aquí está el escenario que modelaremos: si la población excede un cierto límite, entonces ocurre una hambruna y el 99% de la población muere.
¿Cómo podemos hacer esto en InsightMaker? ¡Ya sabes cómo hacer una población en crecimiento exponencial! La nueva característica que aprenderemos hoy es una construcción de programación muy importante: la declaración condicional.
Las declaraciones condicionales también se conocen como declaraciones SI-ENTONCES. En lenguaje sencillo: SI alguna condición es verdadera, ENTONCES haz algo. DE LO CONTRARIO, si alguna otra condición es verdadera, ENTONCES haga otra cosa. ELSE si ninguna de las condiciones anteriores es verdadera, ENTONCES haga otra cosa.
- Conditional statements are also known as IF-THEN statements. In plain English: IF some condition is true, THEN do something. ELSE if some other condition is true, THEN do something else. ELSE if none of the previous conditions are true, THEN do something else.
En el ejercicio de hoy en clase, implementaremos la siguiente declaración condicional (la “condición de hambruna”): SI la población humana está por debajo del límite de población, ENTONCES la tasa de mortalidad anual es 0.01. ELSE si la población excede el límite de población, surge una hambruna y la tasa de mortalidad salta a 0,99
- In today’s in-class exercise, we will implement the following conditional statement (the “famine condition”): IF human population is below the population limit, THEN the annual death rate is 0.01. ELSE if the population exceeds the population limit, a famine arises and the mortality rate jumps to 0.99
Para implementar esto en InsightMaker, necesitamos usar la siguiente sintaxis:
To implement this in InsightMaker, we need to use the following syntax:
If [Humans]<[Limit] Then
0.01
Else
0.99
End If- Elabore un modelo básico de crecimiento exponencial para una nueva [población] llamada Humanos (o simplemente clone y modifique un modelo básico de crecimiento exponencial con tasa de natalidad y mortalidad). Este [Stock] debe tener dos [Flows], uno [Flujo de entrada] llamado Nacimientos y uno [Flujo de salida] llamado Muertes. Tanto Nacimientos como Muertes deben definirse como el producto de Humanos y las constantes de tasa per cápita, respectivamente llamadas Tasa de natalidad y Tasa de mortalidad (cada una definida en el lienzo como [Variables]). Este modelo es idéntico al que hiciste en el laboratorio la semana pasada.
- Put together a basic exponential-growth model for a new [Stock] named Humans (or just clone and modify a basic exponential growth model with birth and death rate). This [Stock] should have two [Flows], one [Flow In] named Births and one [Flow Out] named Deaths. Both Births and Deaths should be defined as the product of Humans and per-capita rate constants, respectively called Birth rate and Death rate (each defined on the canvas as [Variables]). This model is identical to the one you made in lab last week.
- Inicialice la población de Humanos en 1000. Establezca la Tasa de natalidad en 0.1 (humanos producidos por humano por año). Establezca la Tasa de muerte en 0.01 (humanos perdidos por humano por año). Cambie la configuración para que la simulación se ejecute durante 100 años.
- Initialize the population of Humans to 1000. Set the Birth rate to 0.1 (humans produced per human per year). Set the Death rate to 0.01 (humans lost per human per year). Change the settings so that the simulation runs for 100 years.
- Ejecute este modelo, asegúrese de que se comporte como lo esperaría (¡produciendo un crecimiento exponencial!). ¿Cuántos humanos hay después de 100 años?
- Run this model, make sure it behaves like you would expect it to (yielding exponential growth!). How many humans are there after 100 years?
- Ahora cree un nuevo [Stock] llamado Limit , que represente el límite de población para Humanos. Esto podría, por ejemplo, representar el número máximo de seres humanos que podrían mantenerse indefinidamente si toda la tierra cultivable se cultivara con el cultivo más rico en energía posible. Inicialice el “Límite” a medio millón.
- Now make a new [Stock] called Limit, representing the population limit for Humans. This could, for instance, represent the maximum number of humans that could be supported indefinitely if all arable land were cultivated with the most energy-rich crop possible. Initialize the “Limit” to half a million.
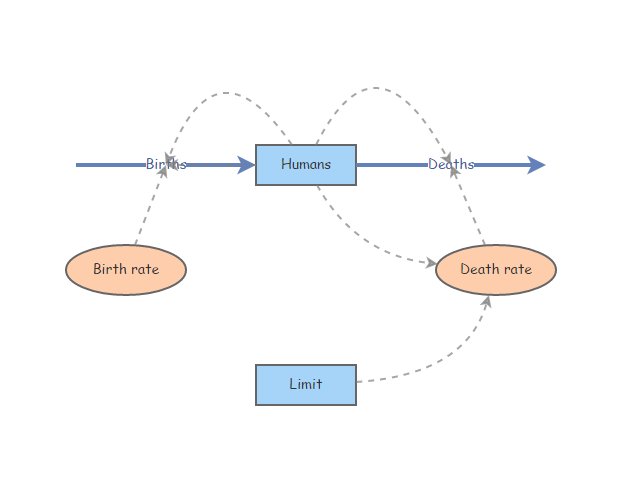
- En preparación para implementar la condición de “hambruna” (la tasa de mortalidad aumenta al 99% si Humanos excede el Límite), cree nuevos **Links* desde Humanos a Tasa de mortalidad y desde Límite a Índice de mortalidad. Su lienzo debe verse como la imagen a continuación:
- In preparation for implementing the “famine” condition (death rate increases to 99% if Humans exceeds Limit), create new Links from Humans to Death rate and from Limit to Death rate. Your canvas should look something like the image below:
- ¡Ahora podemos implementar la “condición de hambruna”! Abra la ventana del editor de ecuaciones para * Tasa de mortalidad * (haga clic en el signo igual) y escriba lo siguiente:
- Now we can implement the “famine condition”! Open the equation editor window for Death rate (click on the equals sign) and type the following:
If [Humans]<[Limit] Then
0.01
Else
0.99
End IfEn realidad, no es necesario que escriba todo esto, simplemente haga clic en “Funciones de programación” en el editor de ecuaciones y seleccione “Si-Entonces-Else” de las opciones. Siempre es mejor usar los generadores de sintaxis integrados, ya que eso evita que cometa errores de sintaxis no intencionales (¡que pueden ser difíciles de eliminar!).
- Ejecute el modelo y describa lo que sucede.
Pregunta de debate ¿esta población está regulada?
RETO: Malthus dijo que “La población, cuando no se controla, aumenta en una proporción geométrica. La subsistencia aumenta solo en una proporción aritmética”. Con esto quiso decir que las poblaciones crecen exponencialmente, mientras que los límites de población (capacidad de producción de alimentos) crecen linealmente.
¿Qué sucede si se permite que el límite aumente aritméticamente? Intente implementar esto en InsightMaker. Es decir, ¿puede cambiar el modelo para que el límite de población aumente linealmente, digamos, en 1000 por año? ¿Qué pasa entonces? SUGERENCIA: ¡puede agregar un [Flow] para representar un aumento en la producción agrícola!
Q ¿Puede ajustar los parámetros para que esta población humana simulada sea sostenible? ¿Por qué? ¿Por qué no? [Edmodo]
Para diversión, aquí hay un Video made by John Green sobre Malthus y el crecimiento poblacional!
… Otro video video sobre el influyente libro de 1972, “Limits to Growth”, lo que hizo el argumento de que el crecimiento no es sostenible: ¡la tierra tiene límites! ¿Te suena familiar este argumento? Curiosamente, el modelo Insightmaker “World3” que algunos de ustedes pueden haber sacado en nuestra primera semana de clase es la base de las terribles predicciones del libro “Limits to Growth”.