Metapoblaciones: Metapopulations
BIOL4558
Agosto 2021
Metapoblaciones
Ahora que estamos pensando en animales/plantas que viven en áreas particulares del espacio, ¡debemos empezar a pensar en ecología de movimiento además de ecología de población ! Los parches de una metapoblación se conectan mediante dispersión . Si no hubiera conectividad (dispersión entre parches), no sería realmente una metapoblación, sino un conjunto de poblaciones aisladas que podría modelar de forma independiente.
Incluir un proceso de dispersión nos permite (¡finalmente!) Pensar en toda la ecuación “BIDE”.
\(\Delta N = B + I - D - E\)
Pero, de hecho, muchos modelos de metapoblaciones (‘metapoblaciones clásicas’, cubiertas en esta conferencia y en el Capítulo 4 de Gotelli) ¡no consideran a los individuos en absoluto!
¿Qué es una metapoblación?
En ecología de metapoblaciones , generalmente estamos considerando un paisaje con un cierto número de parches de hábitat potencialmente habitables.
Una metapoblación es simplemente una población de parches , cada uno de los cuales puede o no estar ocupado por una especie de interés en un momento dado. Se pueden ocupar diferentes conjuntos de parches en diferentes momentos.
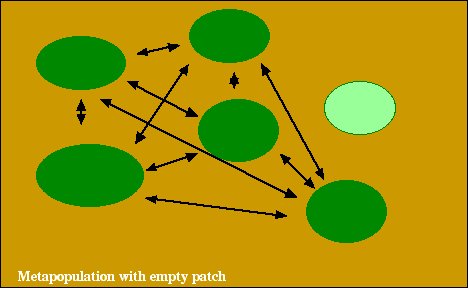

Para simplificar, a menudo asumimos que todas las áreas fuera de un parche son completamente inadecuadas (es decir, NO son un hábitat).
A menudo también asumimos que todos los parches son similares (calidad de hábitat, área y conectividad similares a los parches vecinos) y, por lo tanto, son más o menos intercambiables.
En lugar de realizar un seguimiento de las personas en cada parche (\(N\)), a menudo solo hacemos un seguimiento de la fracción de parches ocupados en nuestro paisaje (\(f\)).
En lugar de realizar un seguimiento de la dispersión de individuos entre parches, solo consideramos la colonización de parches desocupados (vacíos) a través de la inmigración ($I $) y el efecto de rescate (inmigración que previene la extinción de un parche; ver más abajo).
El concepto de la ecología de Metapoblación cubre una amplia gama de escenarios,
- siempre que haya parches de hábitat distintos en un paisaje, y
- siempre que haya alguna dispersión entre parches, entonces es un tipo de metapoblación.
Cuando hay una tasa muy alta de dispersión (y apareamiento) entre parches, la metapoblación se describe como “panmíctica” (conectividad genética perfecta).
NOTA: en algunas definiciones (incluso para metapoblaciones ‘clásicas’), una “metapoblación” se define de manera más estricta como un conjunto de parches con conectividad limitada con al menos algunos parches desocupados en algunos momentos. ¡Prefiero la definición más inclusiva!
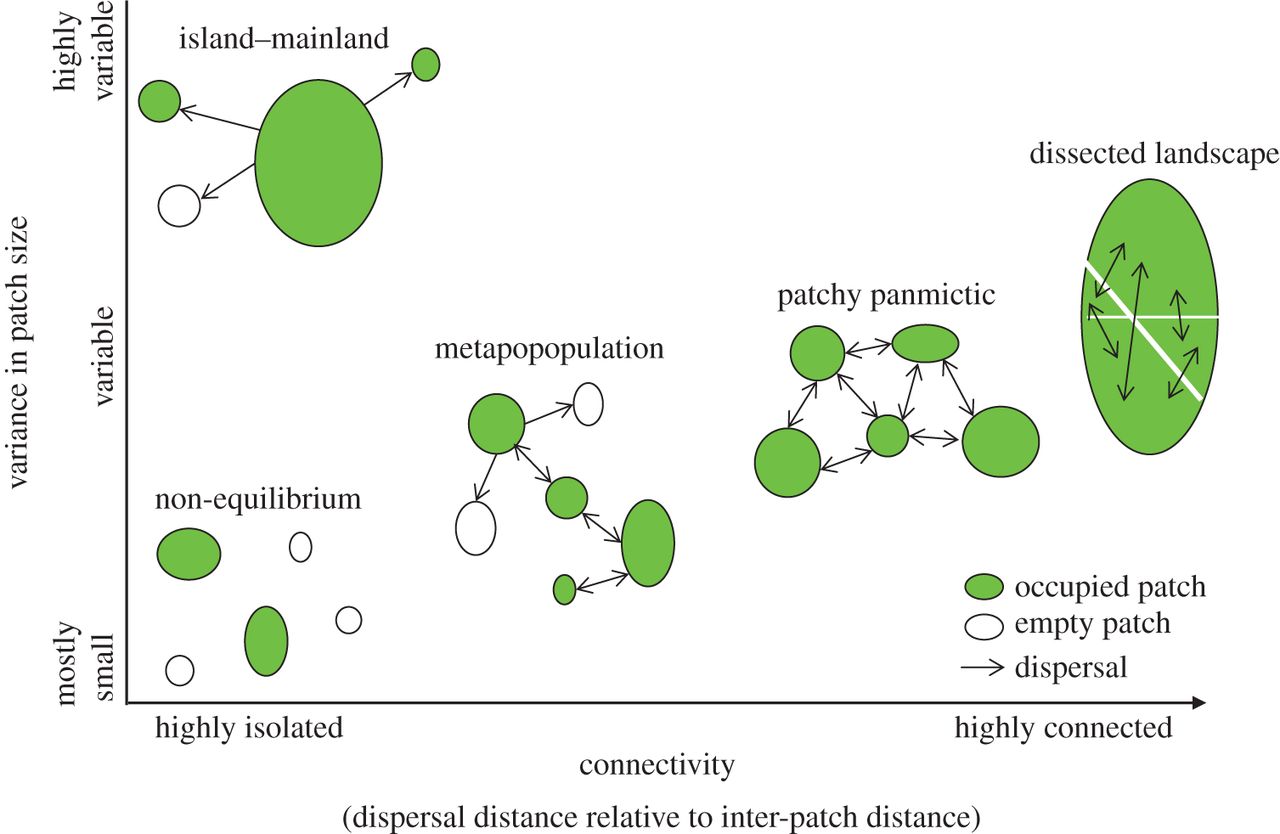
Aunque el término “metapoblación” se utiliza a menudo para referirse a modelos en los que no nos importa la abundancia (solo consideramos ** ocupación de parches **, como los modelos del Capítulo 4 de Gotelli), podemos realizar un seguimiento de la abundancia de parches en un modelo de metapoblación si realmente queremos! De hecho, si queremos, cada parche puede contener una población dependiente de la densidad estructurada por etapas. O puede contener un conjunto de individuos, como en un modelo basado en individuos.
Aunque no los heremos en esta clase pueden tener la oportunidad de usar un modelo de metapoblación en el laboratorio 6 que es mucho más complejo que los modelos del capítulo 4 de Gotelli en el website de Shoemaker!
Modelos de metapoblación “clásicos”
El tipo más simple de modelo de población estructurado espacialmente es el modelo de metapoblación “clásico”.
El concepto de metapoblación fue introducido por primera vez por el ecologista Richard Levins en 1969 (June 1, 1930 – January 19, 2016), y desarrollado por Ilkka Hanski(14 February 1953 – 10 May 2016) entre otros.
En una metapoblación clásica, los parches están ocupados (codificados como 1) o desocupados (codificados como 0) en cualquier momento dado. No consideramos la abundancia, \(N\) en estos modelos; solo hacemos un seguimiento de si cada parche está ocupado o no, y cuántos parches ocupados totales tenemos en nuestra metapoblación en cada paso de tiempo.
That is, the [Stock] we are studying now is NOT the total number of individuals but instead it is the total number of occupied patches (or the fraction of patches occupied)!
En lugar de investigar la dinámica de la población, estamos investigando la dinámica de ocupación de la metapoblación. Es decir, cómo cambia el número de parches ocupados (o la fracción de parches ocupados) con el tiempo.
Bajo el modelo clásico, NO es una metapoblación a menos que algunos parches estén desocupados en algún momento.
P: ¿cómo crece una metapoblación?
P: ¿cómo se reduce una metapoblación?
P: ¿cuál es el equivalente de la estocasticidad demográfica en un modelo de metapoblación? [Edmodo]
La colonización es el proceso de transición de un parche de desocupado a ocupado.
¿Cómo se puede colonizar un parche? La respuesta es inmigración, por supuesto. ¡Esa parte de la ecuación “BIDE” que hemos estado ignorando hasta ahora!
extirpación (o extinción) es el proceso de transición de un parche de ocupado a desocupado.
extinción regional (o global) representa la extinción (extirpación) de todos los parches en la metapoblación.
Más formalmente, aquí hay algunos términos que consideraremos:
\(f_t\) es la fracción, o proporción, de parches que están ocupados en el momento \(t\). Esto también se conoce como tasa de ocupación . Este es el [Stock] primario que modelamos en un modelo de metapoblación clásico.
\(I\) es la fracción total de parcelas colonizadas por inmigrantes por período de tiempo (tasa de colonización o tasa de “inmigración”).
$E $ es la fracción total de parches que se extirpan por período de tiempo (tasa de extirpación).
Por tanto, el cambio de ocupación se puede expresar como:
\(\Delta f = I - E\)
\(p_i\) es la probabilidad de colonización de cualquier parche ocupado a un parche no ocupado.
\(p_e\) es la probabilidad de extinción de cualquier parche ocupado
Ahora que tenemos los términos básicos definidos, ¡podemos construir un modelo básico de dinámica de metapoblaciones! Haremos esto en el laboratorio; consulte el metapopulation lab for more details!
Supuestos del modelo clásico de metapoblación:
- Parches homogéneos (todos los parches se consideran iguales e intercambiables; no difieren en tamaño o calidad; se ignoran las diferencias en la calidad del hábitat o el contexto espacial dentro de los parches).
- La extinción y la colonización son insensibles al contexto espacial, el contexto espacial, o “efectos de vecindad”, no afectan a \(p_e\) y \(p_i\).
- Sin demoras el crecimiento de la metapoblación responde instantáneamente a cualquier cambio en \(f\).
- Gran cantidad de parches incluso cuando la fracción de parches ocupados \(f\) es muy pequeña, ¡la metapoblación clásica aún persiste!. Es decir, ¡la extinción global no es posible!
Claramente, este no es un modelo muy realista, pero es un punto de partida útil. Entonces … comenzaremos haciendo estas suposiciones, ¡pero luego “relajaremos” algunas de ellas!
Variant #1: modelo isla-continente: island-mainland model
La colonización se produce a través de la inmigración de una fuente externa constante: una constante lluvia de propágulos .
Este es el modelo de metapoblación más simple, \(p_i\) y \(p_e\) son constantes.
Variant #2: colonización interna: internal colonization
Ahora, la colonización solo puede ocurrir a través de la inmigración desde dentro de la propia metapoblación. Entonces, cuando se coloniza una pequeña fracción de parcelas, la probabilidad de colonización es baja debido a la falta de inmigrantes potenciales dentro de la metapoblación.
\[p_i = i\cdot f\]
Donde \(i\) representa la fuerza de la inmigración interna cuánto aumenta la probabilidad de colonización con cada nuevo parche ocupado en la metapoblación.
Otra forma de pensar en \(i\) en este modelo es la tasa máxima de colonización exitosa de un parche desocupado cuando casi todos los parches de la metapoblación están ocupados.
Variant #3: efecto de rescate: rescue effect.
¡Ahora, la tasa de extinción puede reducirse mediante la inmigración de otras poblaciones en la metapoblación!
P : ¿tiene sentido esto? ¿Cómo funciona el efecto rescate?
\[p_e = e(1-f)\]
Donde \(e\) representa la fuerza del efecto de rescate. Más concretamente, \(e\) representa la tasa máxima de extinción cuando casi todos los parches están vacíos, por lo que el efecto de rescate es insignificante. Y \(e\) representa la fuerza del efecto de rescate. Más concretamente, \(e\) representa la tasa máxima de extinción cuando casi todos los parches están vacíos, por lo que el efecto de rescate es insignificante.
Estabilidad ‘dinámica’: ‘Dynamic’ stability
En el modelo clásico de metapoblación, la extinción no es necesariamente infrecuente. Los parches se extinguen: ¡los parches pequeños pueden ser altamente vulnerables a la estocasiticidad demográfica, como sabemos! - pero mientras los parches puedan volver a colonizarse, podemos alcanzar un equilibrio, donde las extinciones y colonizaciones se anulan mutuamente. En un modelo de metapoblación clásico, se trata de un equilibrio estable, y una metapoblación estable en la que son posibles las extinciones locales, \(p_e> 0\) se denomina dinámicamente estable. Es decir, cualquier parche dado podría extinguirse en un momento dado, pero en general, el tamaño de la metapoblación o sea los parches totales ocupados es relativamente estable y no está en riesgo de extinción regional o global .
El concepto de estabilidad dinámica de la metapoblación, en el que se equilibran las extinciones y las colonizaciones, tiene mucho en común con la estabilidad dinámica de una sola población a la capacidad de carga, en la que cualquier individuo podría morir en cualquier momento, pero las muertes y los nacimientos se equilibran aproximadamente!
¡Distribuyendo el riesgo!
En los modelos clásicos de metapoblación, asumimos una gran cantidad de parches, por lo que no había ninguna posibilidad real de extinción regional/global. Pero la mayoría de las metapoblaciones reales son lo suficientemente pequeñas como para que a menudo debamos considerar el riesgo de extinción global.
Consideremos un sistema en el que una especie ocupa un solo parche, y hay una probabilidad de extinción \(p_e\) de 0.15 por parche por año.
P : ¿Cuál es la probabilidad de extinción regional en algún momento de los próximos 10 años?
La probabilidad de persistencia durante 1 año es \(1-p_e\), por lo que la probabilidad de persistencia durante 10 años es \((1-p_e) ^ {10}\) y la probabilidad de extinción regional es \[1 - ((1-p_e) ^ { 10})\]
Ejemplos
pe=.15 # probabilidad de extincción en un año
1-pe # Probabilidad de persistencia## [1] 0.851-((1-pe)^10) # Probabilidad que un parche vaya a la extinción## [1] 0.8031256.8*.8*.8*.8 # Probabilidad de la extinción de la metapoblación si tiene 4 parches## [1] 0.4096(1-((1-pe)^10))^10 # Probabilidad de la metapoblación ir la extincción si tiene 10 parches## [1] 0.1116438que resulta ser alrededor del 80%. ¡Existe una probabilidad sustancial de extinción regional en algún momento durante los próximos 10 años!
¿Y si hubiera dos parches en lugar de solo uno?
Supongamos que el riesgo de extinción de los dos parches es independiente, es decir, ¡la extinción de un parche no influye en si el otro parche se extingue o no!
Si la probabilidad de extinción de un parche durante los próximos 10 años es 0,8, entonces la probabilidad de que ambos parches se extingan en algún momento durante los próximos 10 años es \(0,8 * 0,8 = 0,64\)
¡¡Entonces la posibilidad de extirpación regional es algo reducida con dos poblaciones !!
Esto es un ejemplo de Distribuyendo el riesgo : spreading the risk.
¿Qué pasa si hay 5 poblaciones independientes en lugar de dos? Entonces, ¿cuál es la probabilidad de extirpación regional en 10 años?
\([1-(1-p_e)^{10}]^5\)
Esto resulta ser alrededor del 33%
¿Qué pasa si hay 15 poblaciones independientes en lugar de cinco? Entonces, ¿cuál es la probabilidad de extirpación regional en 10 años?
\([1-(1-p_e)^{10}]^5\)
Esto resulta ser alrededor del 3%; hemos distribuido efectivamente el riesgo, de modo que a pesar de un riesgo de extinción relativamente alto a nivel de parche, es poco probable que la metapoblación experimente una extinción global.
P : si incluyéramos la dispersión entre parches, ¿la dispersión serviría para reducir aún más el riesgo de extinción global? ¿Por qué o por qué no?
P : ¿Qué pasaría si la extinción de un parche estuviera perfectamente correlacionada con la extinción de todos los demás parches? Si uno se extingue, todos se extinguen.
Fuentes y sumideros: Sources and sinks!
Un concepto importante y prácticamente útil relacionado con las metapoblaciones es el de dinámica fuente-sumidero
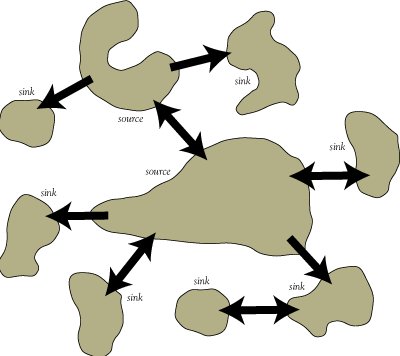
En el mundo real, los parches varían en tamaño y calidad. Es decir, es poco probable que se cumpla el supuesto de homogeneidad de los parches (inherente al marco clásico de la metapoblación) en la mayoría de las metapoblaciones reales.
Al igual que con una población estructurada por edad, donde las tasas vitales y la abundancia de equilibrio pueden variar según la edad o la clase de tamaño, las tasas vitales y las abundancias pueden variar en el espacio. ¡Algunas áreas pueden tener un mejor hábitat, con mayores tasas de crecimiento de la población general! Por otro lado, algunas áreas pueden tener un hábitat pobre, y estas áreas pueden estar asociadas con tasas vitales más bajas …
De hecho, algunos parches pueden tener tan pocos recursos o brindar una protección tan mala contra los depredadores que el crecimiento de la población es negativo, es decir, \(r\) por debajo de cero, o \(\lambda\) menos de 1. Otros parches pueden representar las condiciones perfectas para el crecimiento de la población (al menos si el hábitat no está demasiado poblado).
Una población de origen se define como un parche que proporciona una donación neta de inmigrantes a parches cercanos con hábitat de menor calidad (es decir, poblaciones sumideros o poblaciones pseudo-sumideros). Una población de origen debe persistir indefinidamente, incluso aislada.
Una población sumidero se define como un parche que se extinguiría si no fuera por la entrada constante de inmigrantes de poblaciones de origen cercanas.
P :¿Cómo se relaciona el concepto de población sumidero con el efecto de rescate ?
Una población pseudo-sumidero se define como un parche aumentado artificialmente por inmigrantes de poblaciones de origen cercanas. De forma aislada (en ausencia de una población fuente cercana), un pseudo-sumidero no se extinguiría (¡un verdadero sumidero se extinguiría!), Sino que se asentaría en una abundancia de equilibrio mucho menor (capacidad de carga). Es decir, un pseudo-sumidero mantiene una abundancia de equlibrium por encima de su capacidad de carga debido a la afluencia de inmigrantes de una o más poblaciones de origen cercanas.
Ejercicio en clase: ¡fuentes y sumideros!
En este ejercicio, exploraremos la dinámica fuente-sumidero.
- Primero haga clic en este enlace y clone este modelo de fuente-receptor basado en la población en InsightMaker. Este modelo representa una metapoblación de cuatro parches con una población fuente grande y tres poblaciones sumideros más pequeñas. Las poblaciones de sumideros están ubicadas a diferentes distancias de la población de origen. Aquí está la configuración espacial aproximada de esta metapoblación:
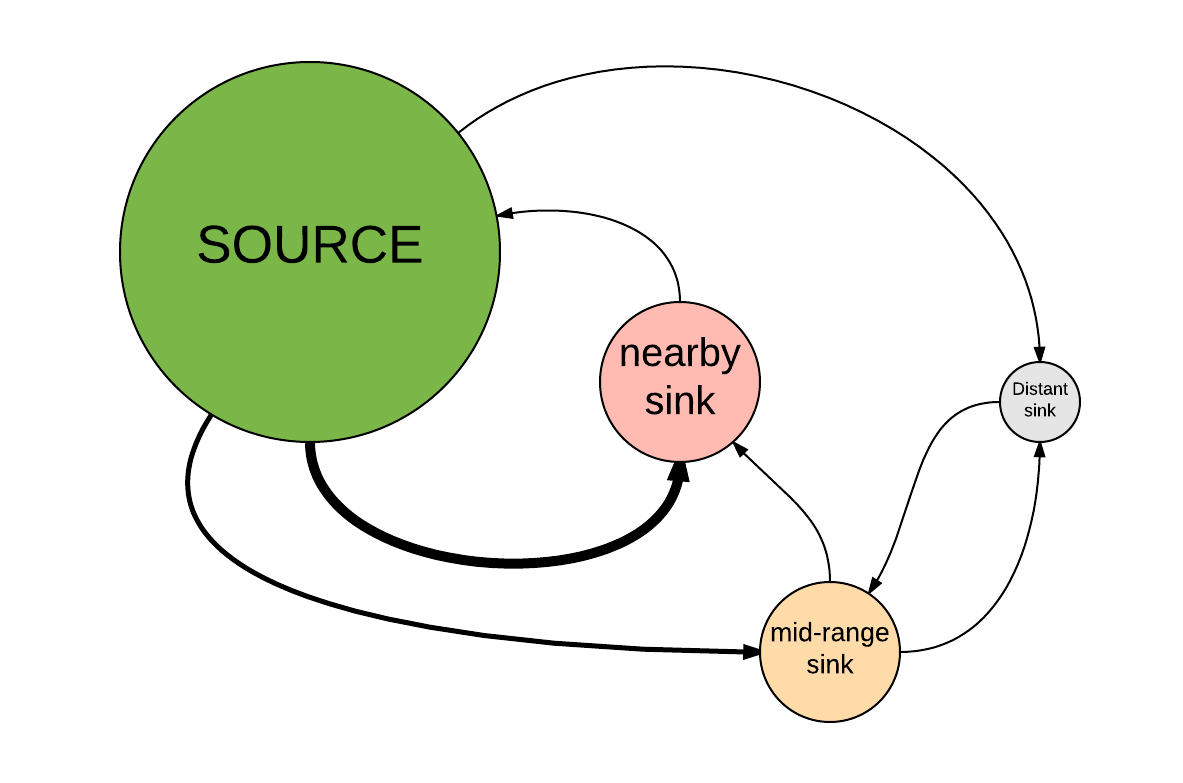
- Asegúrese de que los parámetros del modelo estén en los valores predeterminados. Los parámetros predeterminados deben ser:
- Abundancia inicial en fuente: 100
- Abundancia inicial en sumidero cercano: 10
- Abundancia inicial en sumidero de rango medio: 10
- Abundancia inicial en sumidero distante: 10
- K para la población de origen: 100
- K para sink (Población de sumideros) cercano: 50
- K para sink (Población de sumideros) de gama media: 25
- K para sumidero distante: 15
- Tasa máxima de dispersión: 10% anual (0,1)
- Lambda (tasa de crecimiento discreta) para poblaciones sumideros [lambda malo]: 0,8
- Lambda para la población de origen [lambda buena]: 2.1
NOTA: la tasa de dispersión máxima (en este modelo) es la tasa de dispersión entre parches vecinos. Los parches que se encuentran más separados tienen tasas de dispersión que se calculan como una fracción de la tasa máxima.
- Ejecute el modelo, vea los resultados y asegúrese de comprender cómo funciona.
** Q **: en este escenario, una fracción constante de cada población se dispersa a cada parche vecino cada año.
- ¿Es esto realista?
- ¿Puedes pensar en escenarios del mundo real que conducirían a diferentes patrones de dispersión?
** P **: ¿Qué fuentes de datos podrían ser útiles para comprender las tasas de dispersión en una metapoblación?
- Cambie la tasa de dispersión a cero y ejecute el modelo.
- ¿Lo que sucede? -¿Esto tiene sentido?
- Cambie la tasa de dispersión a 0.01 (1%).
- ¿Que pasa ahora? ¿El sumidero distante sigue funcionando como población sumidero?
- Es decir, ¿está ocupado de forma continua? Si no es así, ¿cuál es la tasa de dispersión mínima que generalmente asegura que el sumidero distante esté constantemente ocupado (continuamente) (asegúrese de que el límite inferior de la región del 95% para la abundancia en este parche sea superior a 2 para todos los años)?
- Vuelva a cambiar la tasa de dispersión al 10%. Ahora reduzca la tasa de crecimiento de la población en la población de origen (“lambda buena”) a 1,1.
- ¿Que pasa ahora? ¿La población fuente todavía opera como una fuente efectiva (es decir, apoya la ocupación constante de todos los sumideros)?
- ¿Qué sucede si establece la tasa de crecimiento máxima en el parche de origen en 1?
- ¿Podría una población así servir alguna vez como una población fuente eficaz?
¡Un pseudo-sumidero!
- Vuelva a cambiar la lambda de origen a 2.1. Ahora cambie la lambda del sumidero a 1.1 y la tasa de dispersión máxima al 25%.
- ¿Cuál es la abundancia de equilibrio aproximada del sumidero distante?
- ¿Cómo se relaciona esto con su capacidad de carga? Genere una figura (utilizando InsightMaker) que ilustre la abundancia del sumidero distante frente a la capacidad de carga (a lo largo del tiempo).
- ¿Cómo ilustra esta figura el concepto de pseudo-sumidero ?
¡Una trampa ecológica!
- Vuelva a cambiar todos los parámetros a sus valores predeterminados. Ahora considere el siguiente escenario:
NOTA: es posible que desee clonar su modelo ahora para que pueda ir y venir fácilmente entre el modelo de “trampa ecológica” y el modelo de “fuente-sumidero”.
¡La población “sink” (Población de sumideros) cercano es ahora extremadamente atractivo para nuestra especie focal, ya que contiene abundantes recursos alimenticios y lo que parece un buen refugio! Sin embargo, en este hábitat también hay un nuevo depredador introducido que la especie no puede detectar. Por lo tanto, las tasas de dispersión al hábitat del sumidero son muy altas, pero las tasas de mortalidad también son muy altas.
Para forzar a un número desproporcionado de personas a ingresar al sumidero cercano, abra el editor de ecuaciones para el flujo desde la fuente al sumidero cercano. Cambie la primera línea para que lea:
0.01*[nearby sink] - 0.5*[SOURCE]NOTA: puede “comentar” lo que estaba anteriormente en el editor de ecuaciones para este flujo. Para hacer esto, puede usar símbolos de almohadilla como lo hemos hecho en el pasado (¡y como R!) O podemos poner entre corchetes un bloque completo de código usando la siguiente sintaxis:
/ *
algunos al azar
codificar aquí
y
algo mas
codigo aleatorio
* /¡Esto obligará al 50% de la población de origen a intentar trasladarse al hábitat del sumidero cada año! Casi todos los individuos que se encuentran en el hábitat del sumidero intentarán permanecer allí.
Además, cambie la lambda para el sumidero cercano a 0.25, (lo que significa que el 75% de la población de sumideros muere cada año debido a la depredación). Para hacer esto, reemplace el término [lambda malo] en el flujo de nacimientos / muertes para el sumidero cercano con el número “0.25”. Abra el editor de ecuaciones para este flujo; después de cambiar, debería verse así:
growth <- [nearby sink]*Ln(0.25)
totalexp <- [nearby sink]+growth # expected population size
newexp <- 0
If totalexp>0.5 Then
newexp <- RandPoisson(totalexp)
End If
newexp-[nearby sink]
- Ejecute el modelo con el “Sink patch” (Población de sumideros) cercano como trampa ecológica e intente abordar las siguientes preguntas:
** P **:
- ¿de qué manera el sumidero cercano es ahora una trampa ecológica ?
- ¿Son todas las poblaciones de sumideros realmente trampas ecológicas ?
** P **: ¿Están mejor las metapoblaciones sin poblaciones sumideros?
- ¿Podría ser deseable eliminar una población sumidero para mejorar el estado de conservación de una metapoblación?
- ¿Bajo que circunstancias?
- ¿Cómo se relaciona esto con el concepto de *dependencia de la densidad?
¡Beneficios de las poblaciones de sumideros!
¡Es posible que las poblaciones de sumideros no siempre sean tan malas para la conservación! Considere el siguiente escenario:
Una gran población de origen puede mantener un conjunto de 3 poblaciones satélite, cada una de las cuales no persistiría en ausencia de dispersión de la población de origen. Ocasionalmente (por ejemplo, una vez cada 100 años), un incendio catastrófico erradica la población fuente. Sin embargo, la población de origen es colonizada por individuos que migran de las poblaciones satélites (sumideros). ¡En ausencia de las poblaciones de sumideros, es casi seguro que toda la metapoblación se extinguiría! #### ¡Beneficios de las poblaciones de sumideros!
In-class exercise: sources and sinks (Población sumideros)!
In this exercise, we will explore source-sink dynamics!
- First click on this link and clone this population-based source-sink model in InsightMaker. This model represents a four-patch metapopulation with one large source population and three smaller sink populations. The sink populations are located at varying distances from the source population. Here is the approximate spatial configuration of this metapopulation:

- Make sure the model parameters are at default values. The default parameters should be:
Initial abundance in source: 100
Initial abundance in nearby sink: 10
Initial abundance in mid-range sink: 10
Initial abundance in distant sink: 10
K for source population: 100
K for nearby sink: 50
K for mid-range sink: 25
K for distant sink: 15
Maximum dispersal rate: 10% per year (0.1)
Lambda (discrete growth rate) for sink populations [lambda bad]:
0.8
Lambda for source population [lambda good]: 2.1
NOTE: maximum dispersal rate (in this model) is the rate of dispersal between neighboring patches. Patches that are located farther apart have dispersal rates that are computed as a fraction of the maximum rate.
- Run the model, view the results and make sure you understand how the model works.
Q: in this scenario, a constant fraction of each population disperses to each neighboring patch each year. Is this realistic? Can you think of real-world scenarios that would lead to different dispersal patterns?
Q: what data sources might be helpful in understanding dispersal rates in a metapopulation?
Change the dispersal rate to zero and run the model. What happens? Does this make sense?
Change the dispersal rate to 0.01 (1%). What happens now? Does the distant sink still function as a sink population? That is, is it occupied continuously? If not, what is the minimum dispersal rate that generally ensures that the distant sink is consistently (continuously) occupied (make sure the lower bound of the 95% region for abundance in this patch is above 2 for all years)? [tophat]
Change the dispersal rate back to 10%. Now reduce the population growth rate in the source population (“lambda good”) to 1.1. What happens now? Does the source population still operate as an effective source (that is, does it support consistent occupation of all the sinks)? What happens if you set the maximum growth rate in the source patch to 1? Could such a population ever serve as an effective source population?
A pseudo-sink!
- Change the source lambda back to 2.1. Now change the sink lambda to 1.1 and the max dispersal rate to 25%. What is the approximate equilibrium abundance of the distant sink? How does this relate to its carrying capacity? Generate a figure (using InsightMaker) that illustrates the abundance of the distant sink vs. carrying capacity (over time). How does this figure illustrate the concept of a pseudo-sink.
An ecological trap!
- Change all params back to their default values. Now consider the following scenario:
NOTE: you may want to clone your model now to enable you to easily go back and forth between the “ecological trap” model and the “source-sink” model.
The nearby sink patch is now extremely attractive to our focal species- since it contains abundant food resources and what seems like good shelter! However, in this habitat there is also a novel, introduced predator that the species is unable to detect. Therefore, dispersal rates to the sink habitat are very high, but mortality rates are also very high.
To force a disproportionate number of individuals into the nearby sink, open the equation editor for the flow from the source to the nearby sink. Change the first line to read:
0.01*[nearby sink] - 0.5*[SOURCE]NOTE: you can “comment out” what was previously in the equation editor for this flow. To do this, you can either use pound symbols like we have done in the past (and like R!) or we can bracket a whole block of code using the following syntax:
/*
some random
code here
and
some more
random code
*/This will force 50% of the source population to try to move to the sink habitat each year! Nearly all individuals that are in the sink habitat will attempt to stay there.
Also, change the lambda for the nearby sink to 0.25, (meaning 75% of the sink population dies each year due to predation). To do this, replace the [lambda bad] term in the births/deaths flow for the nearby sink with the number “0.25”. Open the equation editor for this flow- after you change, it should look something like this:
growth <- [nearby sink]*Ln(0.25)
totalexp <- [nearby sink]+growth # expected population size newexp <- 0 If totalexp>0.5 Then newexp <- RandPoisson(totalexp) End If newexp-[nearby sink]
- Run the model with the nearby sink as an ecological trap, and try to address the following questions:
Q: in what way is the nearby sink now an ecological trap? Are all sink populations really ecological traps?
Q: are metapopulations better off without sink populations? Could it ever be desirable to remove a sink population to improve the conservation status of a metapopulation? Under what circumstances? How does this relate to the concept of *density-dependence?
Benefits of sink populations!
Sink populations may not always be so bad for conservation! Consider the following scenario:
A large source population is able to maintain a set of 3 satellite populations, each of which would not persist in the absence of dispersal from the source population. Occasionally (e.g., once per 100 years), a catastrophic fire eradicates the source population. However, the source population is then colonized by individuals migrating from the satellite (sink) populations. In the absence of the sink populations, the entire metapopulation would almost certainly go extinct!