Ejemplo: Parametizando un modelo PVA
BIOL4558
Agosto 2021
Estudio de caso de PVA: modelando de la recuperación el “Black-footed ferret” en un sistema vinculado depredador-presa-enfermedad
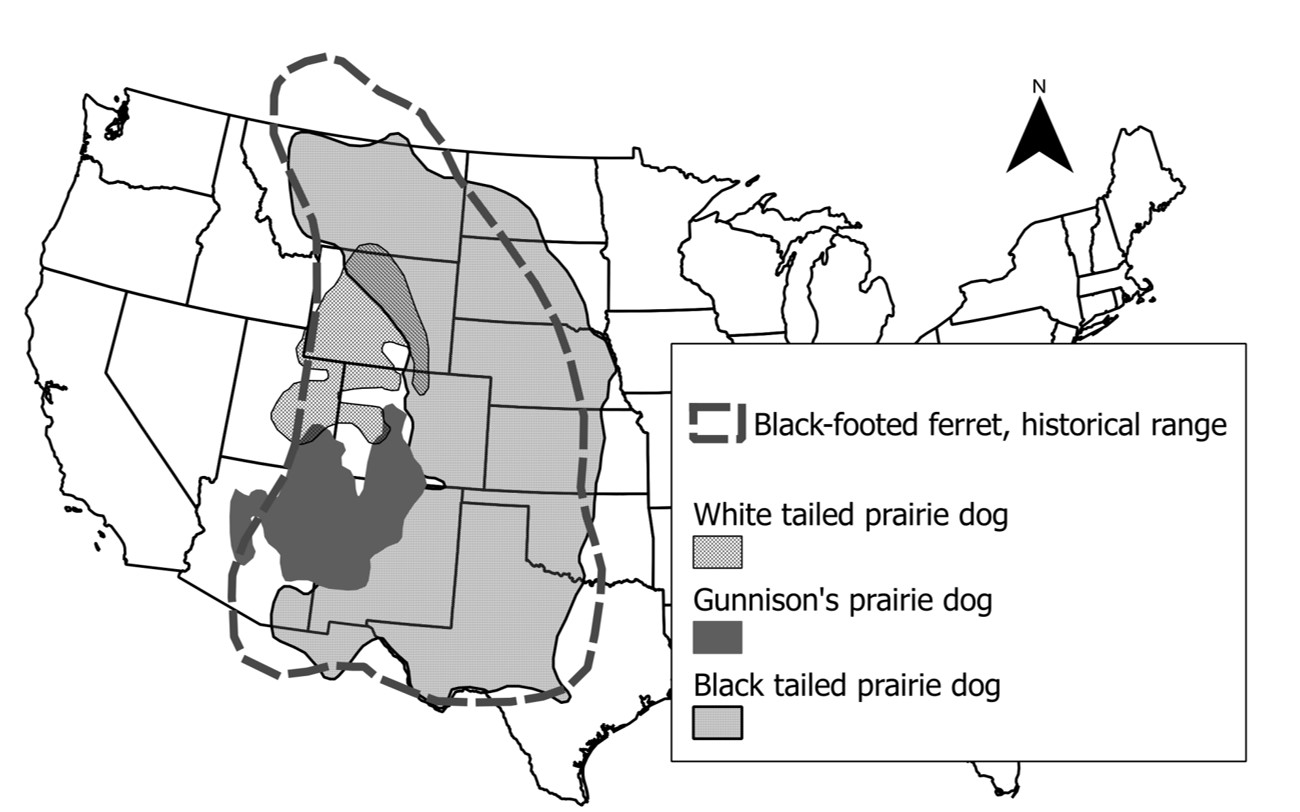
Un depredador obligado
- Aproximadamente el 90% de la dieta del Black-footed ferret consiste en perros de la pradera (depredador obligado).
- Los Black-footed ferret dan a luz en madrigueras de perritos de la pradera.
- La distribución histórica del Black-footed ferret coincide con las tres especies de perritos de la pradera que constituyen su presa.
- No puedes saber qué está pasando con las poblaciones de BFF sin saber qué está pasando con los perros de la pradera

¡Hechos sobre los Black footed ferret!
- Extinto en la naturaleza en 1987
- En 1987, los últimos 18 individuos fueron retirados para críarlos en cautividad.
- Más de 3500 liberados en la naturaleza en 19 ubicaciones en EE. UU., México y Canadá (Livieri 2011)
- Cuatro sitios de reintroducción considerados autosuficientes
Sitio de Estudio: Conata Basin
- Como parte de los esfuerzos de reintroducción de los BFF, se lanzaron 150 kits de BBF nacidos en cautiverio durante un período de 4 años a las colonias de perros de la pradera en la Cuenca de Conata a partir de 1996

Resultados
- Este esfuerzo resultó en una población autosuficiente con un total de aproximadamente 200 animales para el año 2000 (Livieri 2006).
- Establecimiento rápido y libre de plagas de BBF, entre los sitios de reintroducción de BBF más exitosos.
- Disminuyó drásticamente desde que se detectó peste selvática en 2008, pasando de 335 individuos documentados en 2007 a solo 71 en 2012 (Livieri 2012).
- Se han implementado esfuerzos de mitigación de plagas, incluyendo
- tratamiento con insecticida en la madriguera
- vacunación experimental de BBF (Abbott y Rocke 2012).
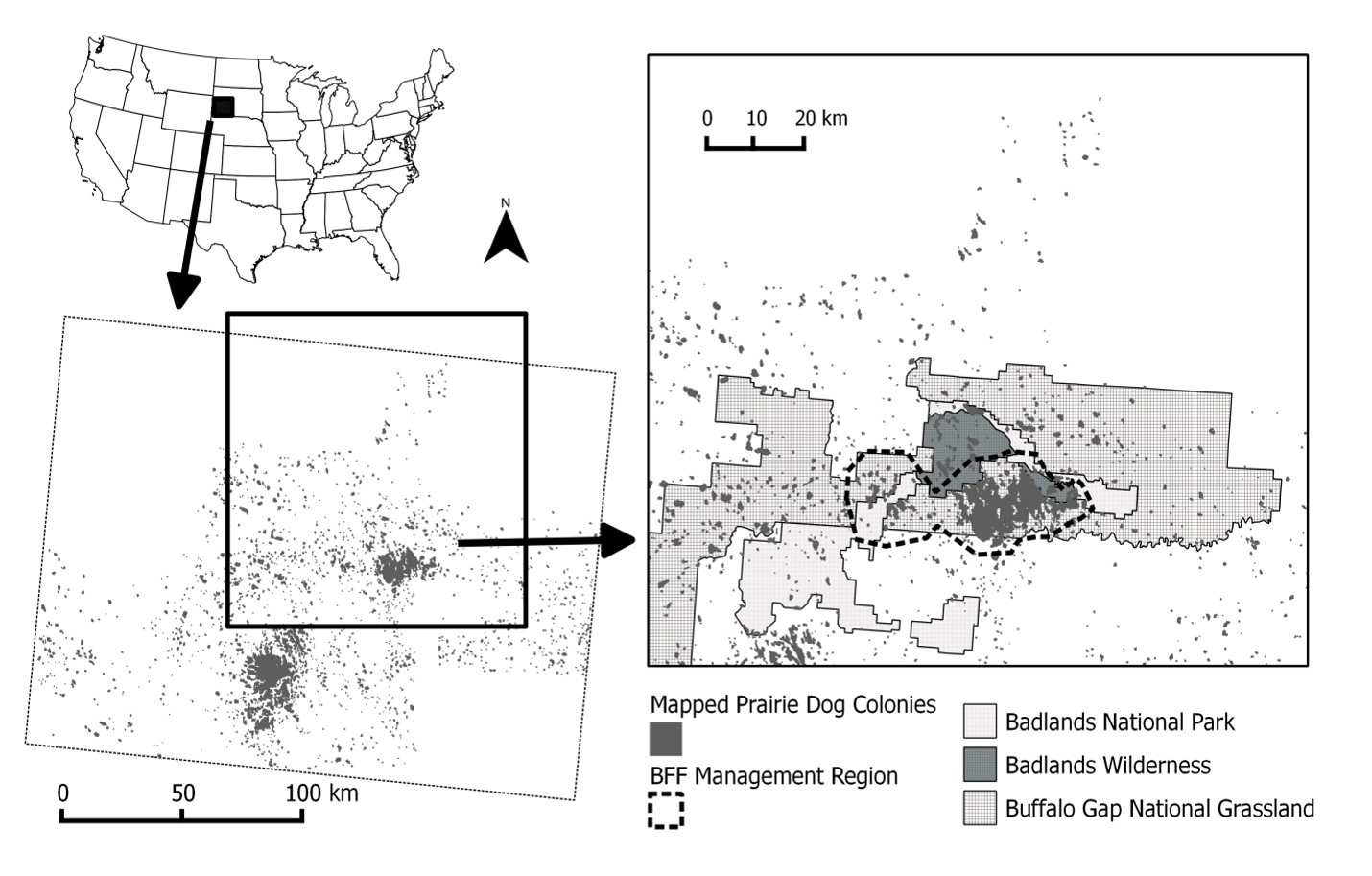
Perritos de la pradera en la Cuenca de Conata y la región circundante

Estructura espacial de la región de estudio

Plaga Silvática
USGS_Sylvatic_Plague - Enfermedad exótica transmitida por pulgas - Altamente fatal para los perros de la pradera (y BBF) - La continua expansión de la plaga hacia con socavar los esfuerzos de recuperación de los BBF. - La peste se observó por primera vez en nuestro sitio de estudio (Cuenca de Conata) en 2008
Un metamodelo” “metamodel”!
- El PVA se centra típicamente en una sola especie.
- ¡Las interacciones entre especies no suelen incluirse explícitamente!
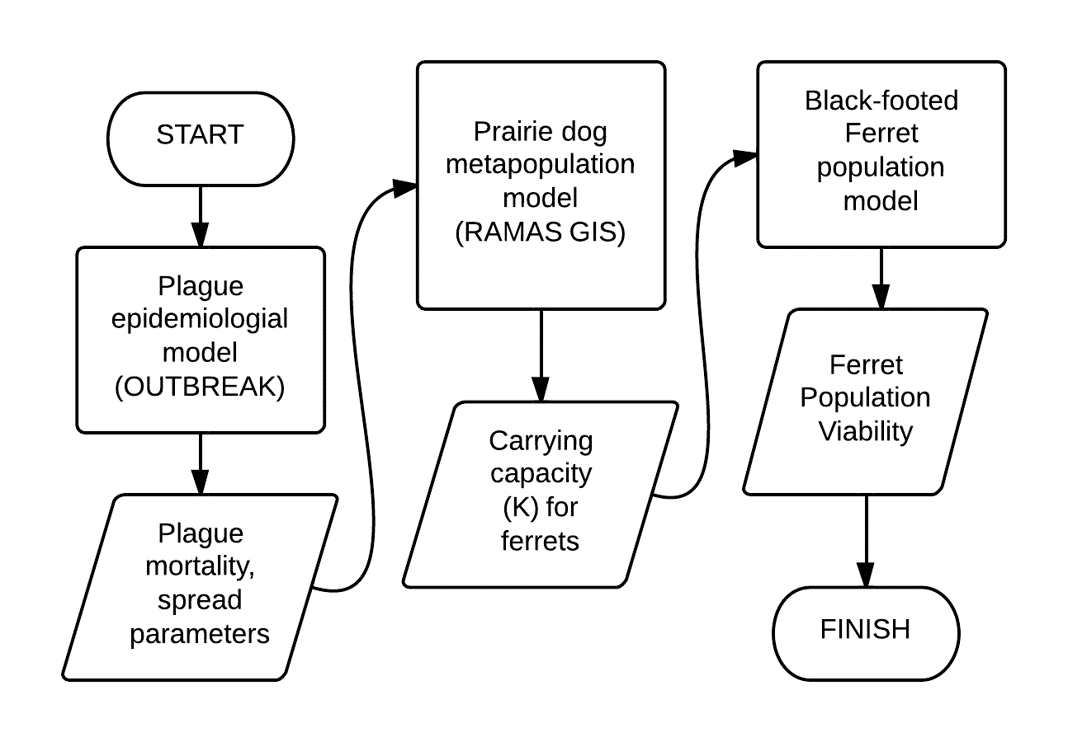
Submodelo de perro de la pradera
- Metapoblación de 1591 colonias
- Amplia gama de abundancia, conectividad entre colonias.
- RAMAS GIS
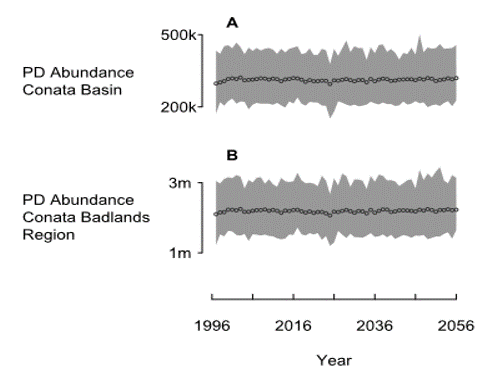
Así es como se ve el modelo del perrito de las praderas en ausencia de plaga. Población robusta con prácticamente ningún riesgo de extinción de los perros de las praderas.
BBF submodel
En ausencia de plaga …
El modelo vinculado depredador-presa-enfermedad …
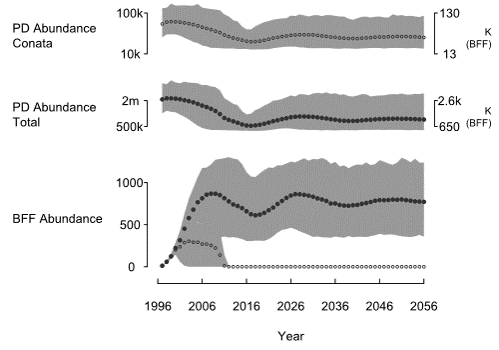
- La población de perros de la pradera declina y se asienta en un nuevo equilibrio inferior.
- La abundancia mínima de Pdogs es de alrededor de 12k para la Cuenca de Conata, lo que realmente es insuficiente para mantener a los BBF.
- La población de BBF se extingue rápidamente si solo pueden acceder a las colonias de Pdog en el área de la Cuenca de Conata.
- Sin embargo, es probable que la población de BBF reintroducida en Conata sea sostenible (dada la presencia de peste) si los BBF pueden acceder a presas fuera de la región actualmente gestionada para hurones (cuenca de Conata).
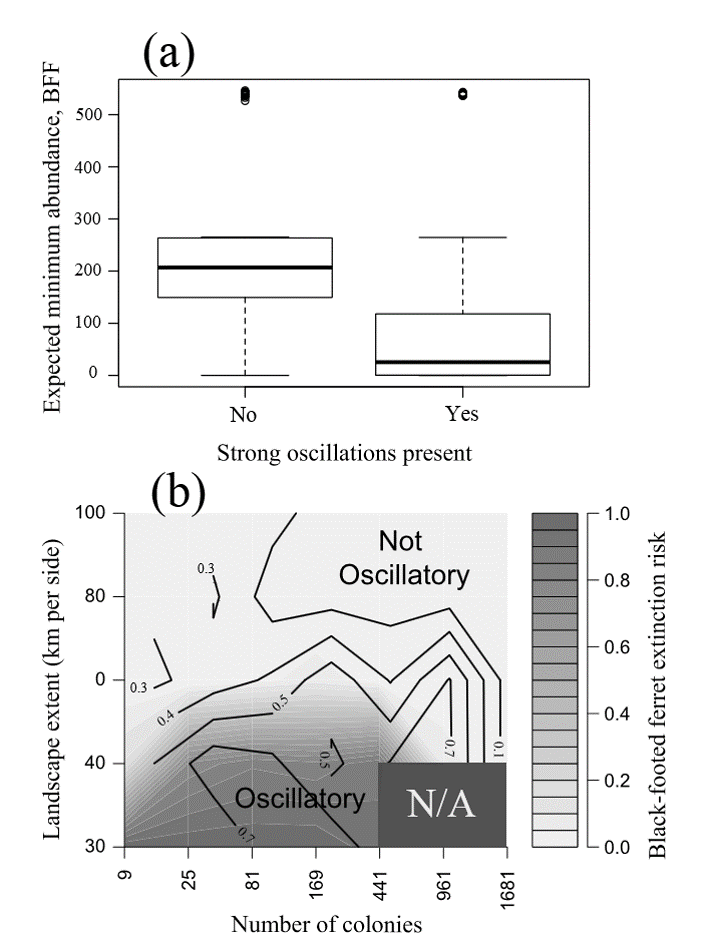
¡Una propiedad emergente!
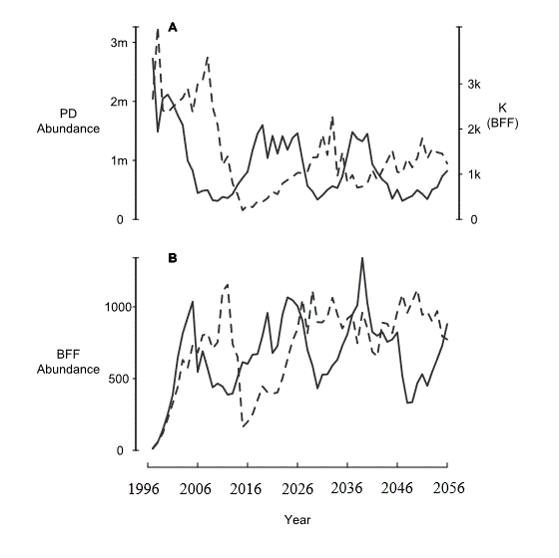
¡La población de BFF y las poblaciones de EP ahora están en ciclo debido a la dinámica de la plaga de EP!
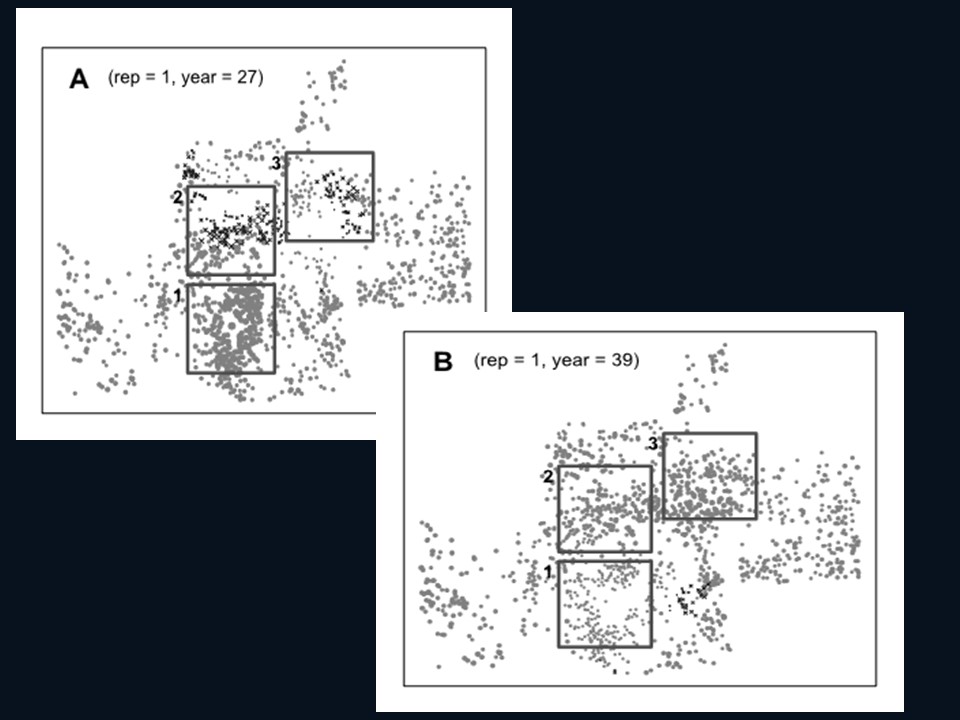
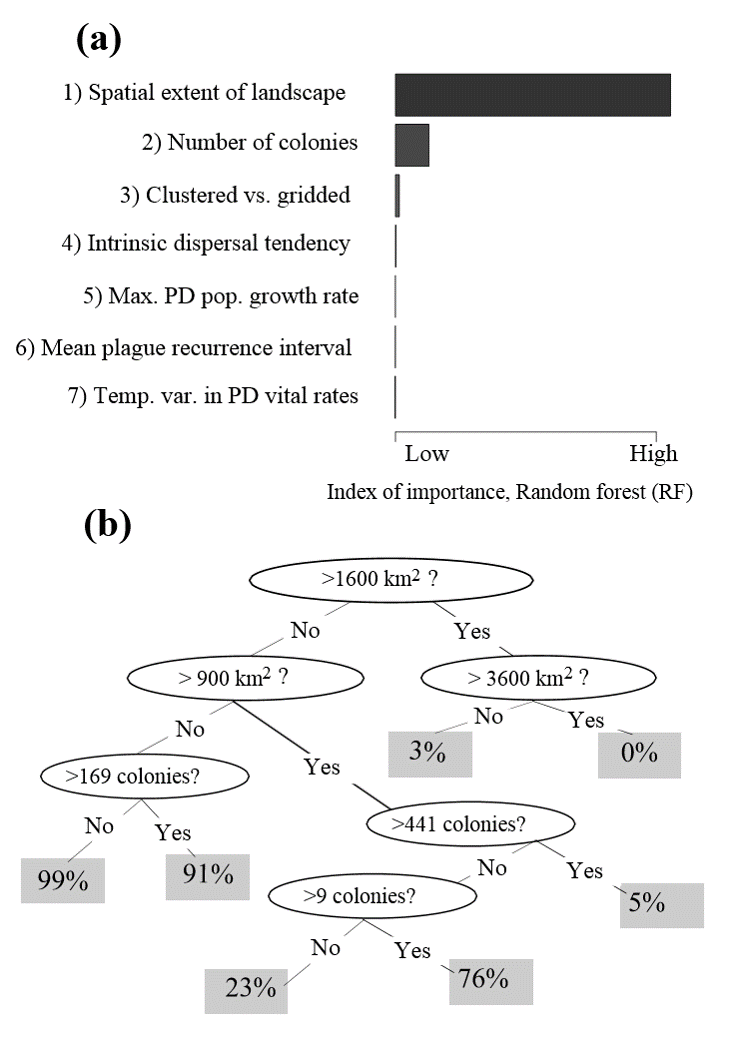
Conclución
- Los BBF pueden requerir paisajes de praderas extensas para persistir a través de epizootias de peste
- Las tasas observadas de propagación de la peste (o la sincronicidad de los brotes de peste) se pueden utilizar para definir la escala espacial en la que es probable que persistan los BBF.
Parametrización detallada: ¡un modelo de metapoblación de perros de la pradera y BBF!
Aquí lo guiaré a través de una parametrización detallada de los modelos de perro de la pradera y hurón (ver el documento here).
Este modelo es más complejo que los modelos que hará para su proyecto final, pero es de esperar que sirva como una ilustración útil de cómo puede justificar sus decisiones sobre cómo construir y parametrizar sus modelos.
Estructura espacial de la región de estudio

La estructura espacial de la metapoblación se basó en la distribución de los perros de la pradera en la * Cuenca de Conata *, un subconjunto de 71 poblaciones de perros de la pradera dentro de la región de Conata / Badlands en Dakota del Sur y que cubre aprox. 500 km2 (Fig. 2; delineado en base a Biggins et al. 2011) es una porción de los Pastizales Nacionales de Buffalo Gap directamente al sur del Parque Nacional Badlands y es administrado por el Servicio Forestal de los Estados Unidos (Fig. 2). Esta área fue elegida a principios de la década de 1990 para la reintroducción de BFF debido a la extensa red de colonias de perros de la pradera de alta densidad ubicadas en tierras públicas (Livieri 2006).
Las colonias de perros de la pradera en Conata Basin, Badlands National Park y Buffalo Gap National Grasslands en el suroeste de Dakota del Sur, EE. UU. (En adelante, la región de Conata / Badlands) fueron mapeadas cada dos años por el Servicio Forestal de EE. UU. Desde 1996-2009 utilizando sistemas de posicionamiento global corregidos diferencialmente (GPS) para conectar las madrigueras más externas de los perros de la pradera en un polígono (Biggins et al. 2006a).
Las colonias de perros de la pradera en las áreas circundantes fueron mapeadas en 2004 utilizando transectos aéreos e imágenes digitales (Sidle et al. 2001, Cooper y Gabriel 2005). Convertimos mapas de colonias de perros de la pradera a mapas ráster binarios (0 = sin hábitat, 1 = hábitat) con un tamaño de celda de 50 m. Reimponemos barreras (por ejemplo, carreteras, tuberías) que se perdieron en el proceso de rasterización.
Usamos la unión de todos los años para definir el hábitat potencial. Usamos una distancia de vecindario de 1 celda (50 m) para definir la estructura de la población (ver Akçakaya 2002 para detalles de cómo RAMAS GIS determina la estructura espacial). Por lo tanto, asumimos que cada colonia es una población biológica distinta, que puede estar conectada a otras poblaciones similares (ver la sección sobre dispersión a continuación). Excluyendo las colonias muy pequeñas con capacidad de carga (K) <100 (ver más abajo), esto dio como resultado 1591 poblaciones de DP que van desde aproximadamente 5 ha hasta 10,000 ha, con un tamaño medio de 16 ha y cubriendo aprox. 20.000 km2 (figura 3).
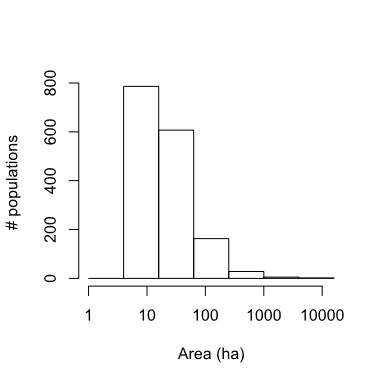
Capacidad de acereo y dependencia de la densidad
La reproducción en los perros de la pradera a menudo está limitada por los recursos (Hoogland 2001), lo que sugiere un efecto dependiente de la densidad de tipo Ricker (scramble) sobre la fecundidad. Por lo tanto, usamos este tipo de dependencia de la densidad y estimamos la tasa de crecimiento máxima (\(R_ {max}\)) basada en el promedio de tasas de crecimiento exponencial exhibidas por varias poblaciones después de choques. Tres de estas tasas fueron después de reducciones debidos a la peste: 1.466 (Biggins et al.2006a, Fig 6.4), 2.024 (Cully y Williams 2001, Fig 4, años 1989-1991) y 3.806 (Cully y Williams 2001, Fig 4, años 1995-1997). Combinamos estas tasas con cuatro tasas de crecimiento después de la peste debidos a otras causas, incluidos disparos, sustancias tóxicas y remoción y translocación (Reeve y Vosburgh 2006, Tabla 10-3, excluyendo las tasas más bajas y más altas, que eran de poblaciones que no se habían sometido a una reducción de población reciente). El promedio de estas 7 tasas de crecimiento exponencial fue 2,44. Para el análisis de sensibilidad, usamos los cuartiles, dando un rango de 1.8 a 2.8. Estos valores coincidieron con una estimación independiente basada en la intersección de la regresión de la tasa de crecimiento de la población ($R \() sobre el tamaño de la población (\) N $) de los datos de Hoogland (1995, Tabla 16.1), que nos dio estimaciones de 2,4 a 3.7, según el tipo de regresión. Dado que la regresión de R sobre N a menudo sobreestima $R_ {max} $, este rango es consistente con la estimación basada en las fases de crecimiento exponencial de las dos poblaciones mencionadas anteriormente.
Asumimos que cada colonia mapeada (ver arriba) representaba una población biológica distinta, con la capacidad de carga (K) definida como una función del área de la colonia y las densidades promedio de los perros de la pradera. En la Cuenca de Conata, la densidad promedio de los perros de la pradera antes de la llegada de la peste era de 28,7 / ha (Livieri 2006). Por lo tanto, multiplicamos el número de células en cada parche por 7.175 (= 28.7x0.25) para calcular la capacidad de carga de ese parche (porque bajo la dependencia de densidad tipo Ricker que usamos, la abundancia promedio sería aproximadamente igual a la abundancia de equilibrio o carga capacidad). Las colonias con K < 100 fueron excluidas del análisis, para disminuir el número de poblaciones y porque las poblaciones muy pequeñas no contribuyen sustancialmente a la dinámica poblacional. Asumimos que las abundancias iniciales eran iguales a K para cada población, y ejecutamos un período de quemado de 10 años para todas las simulaciones para asegurarnos de que todas las colonias estuvieran en equilibrio con su entorno y hubieran alcanzado una distribución de edad estable (S.A.D.).
Estructura demográfica y tasas vitales
Desarrollamos un modelo matricial estructurado por edad y sexo para perros de la pradera utilizando el software RAMAS Metapop (v. 6.0; Akçakaya y Root 2013), con ocho clases de edad de hembras y seis de machos, parametrizadas utilizando tasas de supervivencia y fecundidad extraídas de Hoogland (2001). Parametrizamos la matriz según un censo previo a la reproducción. Usamos tasas de supervivencia basadas en Hoogland (2001, figuras 1a y 2a) y ajustamos una regresión polinomial de la tasa de supervivencia frente a la edad para cada sexo para obtener una función uniforme de la edad (figura 4). Calculamos el tamaño de la camada como 3,1 (de Hoogland 2001, figura 3a). Combinando este valor con la proporción de hembras reproductoras (0,43; Hoogland 2001) y la tasa de supervivencia de los niños de cero años, estimamos la fecundidad en 0,418 hijas y 0,379 hijos por hembra adulta (de 2 años o más) y 0,209 hijas y 0,189 hijos por hembra por año. (1 año). Asumimos un sistema de apareamiento poligínico con cada macho apareamiento con hasta 4 hembras. Debido a que la función de dependencia de la densidad modifica la matriz de la etapa en función del tamaño de la población, los resultados del modelo serían sensibles al valor $R_ {max} $ de la función de dependencia de la densidad, no a los valores exactos de las tasas de supervivencia y fecundidad. Por lo tanto, la sensibilidad a las tasas vitales se modeló a través de la sensibilidad $R_ {max} $ (consulte la sección sobre análisis de sensibilidad, a continuación). Todas las colonias se inicializaron a $K $ y con una distribución de edad estable, y todas las simulaciones se realizaron con un período de quemado de 10 años (para alcanzar un equilibrio aproximado en la metapoblación de perros de la pradera).
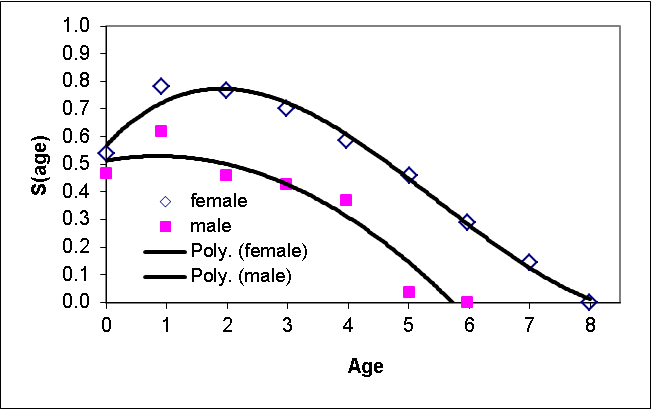
Variabilidad
La variación temporal de las tasas vitales se basa en 14 años de edad y datos del censo específico por sexo de Hoogland (1995, Cuadro 16.1, página 377). Es importante señalar que la población censada ha fluctuado entre 150 y 250 individuos y no parece haberse desplomado debido a la peste u otras razones durante el período de estudio (de lo contrario, agregar la dinámica de la enfermedad sobrestimaría la variabilidad). Para obtener la variabilidad ambiental, eliminamos la varianza demográfica de la varianza observada de las tasas de supervivencia y fecundidad, con base en el binomio esperado y la varianza de Poisson (Akçakaya 2002), y calculamos los coeficientes de variación (Tabla A1-1). Para el análisis de sensibilidad, usamos valores mínimos y máximos basados en bootstrapping (Tabla A1-1).
## Vital_Rate sex CV min_CV max_CV
## 1 Surv F 0.111 0.102 0.119
## 2 Surv M 0.185 0.136 0.201
## 3 Fec F (daughters) 0.350 0.303 0.376
## 4 Fec M (sons) 0.291 0.268 0.331Plaga
Modelamos la dinámica de la plaga dentro de la metapoblación de perritos de la pradera como catástrofes propagadas por dispersores, con virulencia (supervivencia general) y probabilidad por dispersor de iniciar un brote estimado a partir del modelo epidemiológico Brote descrito a continuación (n = 1000 repeticiones). Calculamos la probabilidad de que un dispersor inicie una catástrofe en la población objetivo multiplicando la probabilidad promedio anual de que un individuo (en una población que está experimentando un brote) esté en el estado de enfermedad E (infectado pero aún no infeccioso), con la probabilidad que un solo individuo en el estado de enfermedad E inicia una epizootia de peste que mata al menos a la mitad de la población. Específicamente, el modelo OUTBREAK indicó un 9.3% de probabilidad de que un dispersor individual sea capaz de iniciar la plaga en una nueva colonia (promediado durante todo un año, un perrito de la pradera capaz de dispersarse de una colonia infectada tenía un 9.3% de probabilidad de ser un portador expuesto). ), y un 97% de probabilidad de que tal dispersador inicie una catástrofe, lo que resulta en un 9% de probabilidad por dispersor de iniciar una catástrofe. Cuando se inicia una catástrofe en una población, la tasa de supervivencia se determina, de acuerdo con los resultados del brote, como 2.9% de supervivencia (97.1% de mortalidad) en el año en que se inicia la plaga (sin efectos a largo plazo). Iniciamos el brote de plaga en el año 11, luego de un período libre de plaga de 10 años (a su vez, después del período de quemado de 10 años). reflejando ca. diez años libres de peste en la Cuenca de Conata después de las primeras introducciones de hurones (la peste selvática se detectó por primera vez en la Cuenca de Conata en mayo de 2008; Abbott y Rocke 2012). La peste se inició en la metapoblación de perritos de la pradera asumiendo que (1) la peste se inició en una sola población de perritos de la pradera seleccionada al azar (seleccionada entre poblaciones de tamaño mediano o mayor en la cuenca de Conata), o (2) los brotes de peste surgen espontáneamente con una probabilidad de 0,005 por año por colonia (resultando efectivamente en eventos de iniciación espontánea de la plaga en algún lugar de la metapoblación casi cada dos años). Debido a que RAMAS Metapop calcula el número de dispersores en función de las abundancias posteriores a la plaga, también calculamos el número medio de dispersores infectados (expuestos) en función de la abundancia de colonias final, lo que arroja una estimación del 118% (SE 28%). Por lo tanto, establecemos el parámetro de “probabilidad de infección por dispersor” en Ramas Metapop en su valor máximo del 100% (por lo tanto, se subestima potencialmente la tasa de propagación).
Dispersión
Las tasas de dispersión (proporción de individuos que se dispersan entre cada par de poblaciones definidas) se modelaron en función de las distancias entre el centro y el borde entre las poblaciones, para evitar que poblaciones muy grandes inunden a poblaciones pequeñas a su alrededor. Los perros de la pradera dispersos viajaron una distancia media en línea recta de 2,4 km (Garrett y Franklin 1988). La distancia máxima de dispersión es de 10 km (Knowles 1985 citado en Knowles et al. 2002; Lomolino y Smith 2001). Por lo tanto, usamos una función de distancia de dispersión
\(a \cdot e^{\frac{-D}{b}}=0.083 \cdot e^{\frac{-D}{2.4}}\)
donde D es la distancia desde el centro de la población de origen hasta el borde más cercano de la población objetivo, con una distancia máxima de dispersión de Dmax = 10 km. Calculamos la intersección (el parámetro a) de la siguiente manera. Con base en la estructura espacial de las poblaciones, calculamos el número promedio de vecinos a distancias de 0-0,5 km, 0,5-1 km, 1-2,5 km, 2,5-5 km y 5-10 km. Establecimos la intersección de modo que la tasa total de dispersión esperada de esta población promedio fuera de aproximadamente 0,37, que se calculó como el producto de dos números: (1) 59% de machos de un año que se dispersan de una población de estudio (según los datos informados en las Tablas 1 y 2 en Garrett y Franklin 1988), y (2) tasa de supervivencia relativa de los dispersores (calculada como 0,62, basada en la tasa de supervivencia de 0,9 y 0,56 de los residentes y dispersores según lo informado por Garrett y Franklin 1988). Para el análisis de sensibilidad espacial, usamos un rango de 0.061 a 0.105 para el parámetro a, basado en ± 0.10 para la tasa total esperada de dispersión de la población promedio.
El cálculo anterior se refiere a la tasa de dispersión de los machos de un año. Calculamos la dispersión relativa de otras clases de edad / sexo como 0,46 para las hembras de un año, 0,1 para los machos adultos y 0,39 para las hembras adultas (según los datos informados en las Tablas 1 y 2 en Garrett y Franklin 1988). Estos números son consistentes con las observaciones generales de la dispersión específica por edad y sexo: Hoogland (1995) informó que las hembras de perritos de la pradera generalmente permanecen con su camarilla natal, o se dispersan a largas distancias a otras colonias, pero “la dispersión a corta distancia de las hembras dentro de la colonia de origen casi nunca ocurre”(p. 383); Los perros de la pradera machos, por otro lado, se dispersan a grandes distancias hacia nuevas colonias (principalmente como crías de un año, rara vez como adultos) o a distancias cortas dentro de la colonia de origen.
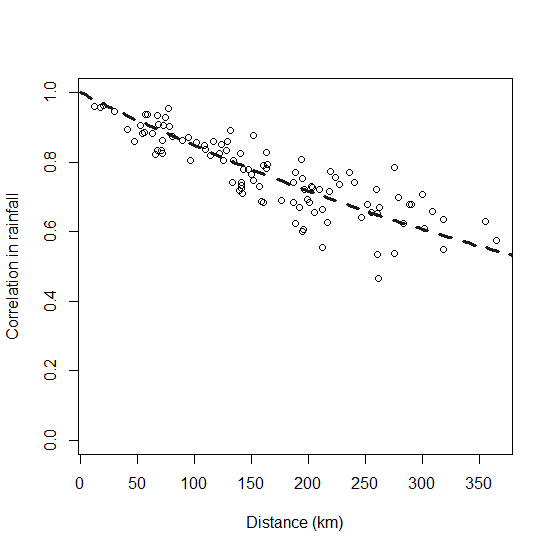
Correlación espacial
La correlación de la dinámica poblacional entre poblaciones se basó en una función de las distancias de centro a centro entre poblaciones. Debido a que las fluctuaciones anuales en las tasas vitales son probablemente una función de las condiciones climáticas, usamos la correlación temporal en las condiciones climáticas como un sustituto para describir la correlación de las fluctuaciones de la población. Específicamente, la autocorrelación espacial en las tasas vitales se modeló como una función de las distancias entre colonias basadas en 30 años de datos de lluvia de verano de 15 sitios extraídos aleatoriamente dentro del rango del perrito de las praderas de cola negra. Ajustamos un modelo exponencial negativo utilizando 30 años de datos de lluvia de verano extraídos de 15 ubicaciones aleatorias en el barrio suroeste de Dakota del Sur (conjunto de datos PRISM; PRISM Climate Group, Oregon State University, http://prism.oregonstate.edu). La ecuación resultante, correlación = exp (-D / 601), donde D es la distancia entre poblaciones, se utilizó para todas las ejecuciones del modelo y no se modificó como parte de los análisis de sensibilidad espacial (Fig. 5).
Modelo de la población de Black-footed Ferret

Estructura demográfica y tasas vitales
Desarrollamos un modelo matricial estructurado por edad y sexo, con 5 clases de edad femeninas y 5 masculinas. Parametrizamos la matriz de acuerdo con un censo posterior a la reproducción, con tasas de supervivencia extraídas de un estudio de recaptura de marcas de Wyoming (Grenier 2008). Las tasas de supervivencia de jóvenes (primer año) y adultos (de un año y mayores) se fijaron en 0,39 (SE 0,17) y 0,67 (SE 0,15), respectivamente. Para el análisis de sensibilidad, utilizamos un rango de 0,22 a 0,56 para la tasa de supervivencia juvenil y de 0,52 a 0,82 para la tasa de supervivencia de adultos, lo que representa un error estándar de la media. La fecundidad juvenil y adulta se estableció en 0,73 y 1,25, respectivamente, según las observaciones de los kits producidos entre 2004 y 2006 (Grenier 2008). Para el análisis de sensibilidad, utilizamos un rango de 0,36 a 0,92 para la fecundidad juvenil y de 0,86 a 1,35 para la fecundidad adulta.
Dependencia de la densidad, capacidad de acarreo y abundancias iniciales
La fuerte dependencia de los BBF sobre los perros de la pradera como presas sugiere una dependencia de la densidad basada en la limitación de recursos y vinculada a la dinámica de los recursos (presas). Por lo tanto, modelamos la dependencia de la densidad del hurón de patas negras con una dependencia de la densidad de tipo Ricker, correspondiente a un modelo de competencia scramble (Brannstrom y Sumpter 2005).
Ejecutamos el modelo de población de hurones de patas negras asumiendo que (1) los BBF solo podían acceder a las colonias de perros de la pradera dentro de la cuenca de Conata, o (2) los hBBF podían acceder a todas las 1591 colonias de perros de la pradera dentro de la región de Conata / Badlands. En el primer caso, asumimos que los BBF solo podían acceder a las colonias de DP dentro de la Cuenca de Conata, una región de aproximadamente 13,000 ha que delineamos como el agregado de las tres sub-unidades de hurones identificadas en Biggins et al. (2011). Por lo tanto, aunque el modelo PD / plaga (ver arriba) cubría un área más grande del suroeste de Dakota del Sur, solo aquellas poblaciones en la Cuenca de Conata estaban vinculadas al modelo del BBF. Debido a que las poblaciones de hurones fueron rápidamente extirpadas por la peste si se limitaban a la cuenca de Conata propiamente dicha, y debido a que la extensión espacial máxima posible para las poblaciones de BBF no está clara (ver texto principal), también ejecutamos escenarios en los que todas las poblaciones de perros de la pradera en Conata -Se suponía que la región de las Tierras Baldías estaba disponible para los BBF como presa.
Calculamos la respuesta funcional de los BBF con base en el modelo de balance energético de Stromberg et al. (1983), quien concluyó (a través de cálculos de rendimiento máximo sostenible) que un área de hábitat capaz de soportar cerca de 766 perros de la BBF para soportar los requisitos mínimos de energía de un solo hurón de patas negras. Por lo tanto, equiparamos una disponibilidad de presas per cápita de 766 perros de la pradera por hurón con una tasa de crecimiento de la población de BBF estable a largo plazo (R = 1, correspondiente a la capacidad de carga en la función de dependencia de la densidad scramble / Ricker en RAMAS Metapop). Por lo tanto, la capacidad de carga (K) de la población de hurones de patas negras se calculó como 1/766 del tamaño de la población de PD en la Cuenca de Conata en cada paso de tiempo. Sin embargo, en años de gran abundancia de perros de la pradera, los BBF suelen mantener territorios que albergan más perros de las praderas de los que necesitan para sobrevivir (Biggins et al. 2006b). En otras palabras, la relación lineal entre la densidad de los perritos de las praderas y la capacidad de carga de los BBF se rompe a altas densidades de perritos de las praderas. Limitamos el valor de K a 462 para la región de Conata con base en la densidad máxima de hurones de 0.04 hurones por ha sugerida por Biggins et al. (2006b). Para el análisis de sensibilidad global, establecimos un tope similar al valor de K para mantener una densidad máxima de 0.04 hurones por ha (por lo tanto, K varió según la extensión del paisaje). Por lo tanto, incluso en años en los que la abundancia de perritos de la pradera es muy alta, la capacidad de carga de la población de hurones simulados no excede el límite máximo dictado por la territorialidad.
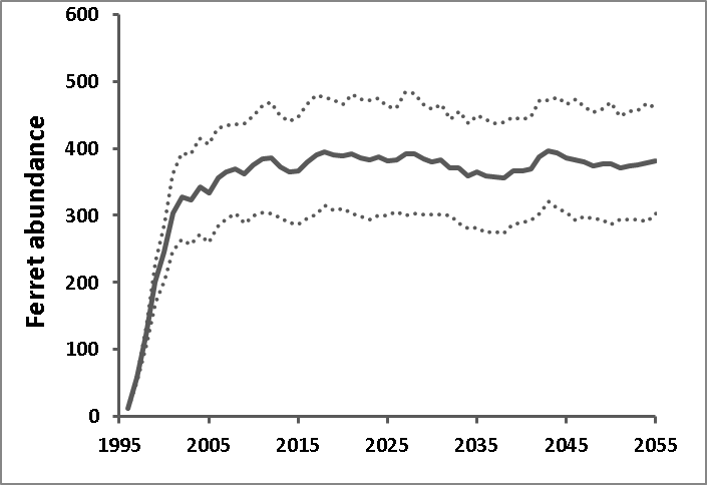
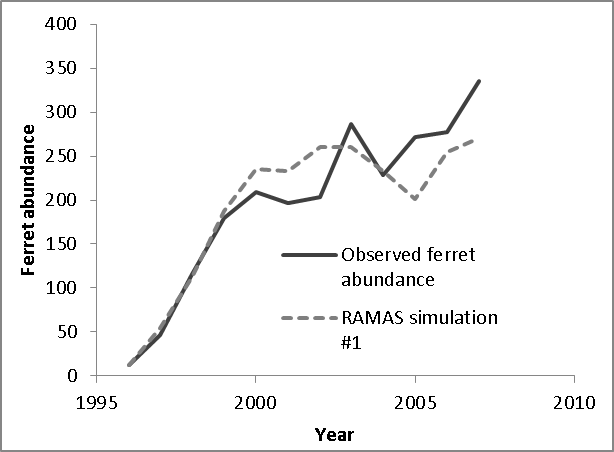
El modelo de balance energético de Stromberg et al. (1983), en el que basamos el vínculo funcional entre la capacidad de carga de los BBF y la abundancia de los perros de la pradera (ver más arriba), asumió que los BBF se alimentaban exclusivamente de los perros de la pradera. Sin embargo, se cree que un componente pequeño pero no dnegligente (aproximadamente el 10%) de la dieta del BBF comprende presas alternativas como ratones y lagomorfos (conejos) (Campbell et al. 1987). La existencia de especies de presas alternativas plantea la posibilidad de que nuestros modelos sobreestimen la disponibilidad de presas per cápita necesaria para adaptarse al crecimiento estable de la población de hurones. Sin embargo, los perros de la pradera son consumidos por muchas especies además del BBF (incluidos tejones, gatos monteses y coyotes; Hoogland 1995), lo que aumenta la posibilidad de que nuestro modelo subestime el número de perros de la pradera necesarios para mantener una población de BBF. Claramente, existe una gran incertidumbre en torno a esta estimación, y estamos planeando un estudio de seguimiento para probar la sensibilidad del sistema BBF / perro de la pradera a las caracterizaciones alternativas de la respuesta funcional y numérica. No obstante, una capacidad de carga de BBF estimada de 485 en la Cuenca de Conata, calculada como 1/766 de la capacidad de carga total estimada de perritos de la pradera, es consistente con el crecimiento observado de la población de BBF reintroducidos en la Cuenca de Conata, que estaba comenzando a estabilizarse en abundancias ca. 350 antes de la llegada de la peste en 2007 (Livieri 2006; Fig. 6).
Establecimos la tasa de crecimiento máxima (Rmax) en 1,48, con base en el promedio de dos estimaciones de la tasa de crecimiento (exponencial) en una población de Wyoming (Grenier et al. 2007). Una estimación es 1.35, el valor propio de la matriz ajustada a los datos de marcado-recaptura, y la otra estimación es 1.60, la tasa (escalar) de crecimiento en el número mínimo de BBF vivos de 2000 a 2006. Para el análisis de sensibilidad, usamos estos dos valores.
La abundancia de BBF para cada iteración se inicializó utilizando eventos de reintroducción conocidos en la Cuenca de Conata, como lo describe Livieri (2006; es decir, las fechas y edades de las liberaciones se modelaron explícitamente). La viabilidad de la población de BBF se resumió utilizando tres métricas: riesgo de cuasi extinción (definido como la proporción de ejecuciones de simulación que caen por debajo de 5 individuos en el año 60 de la simulación), abundancia mínima esperada (definida como la abundancia mínima después del año 10 de la trayectoria promediada durante todas las 1000 simulaciones; McCarthy y Thompson 2001), y la abundancia final media (en el año 60).
Variabilidad
Estimamos la variabilidad temporal en las tasas vitales de los hurones (es decir, la variabilidad no debida a las fluctuaciones en la base de la presa, que se modeló explícitamente a través de la variación en K) ejecutando el metamodelo vinculado BBF/ perro de la pradera para la cuenca de Conata en condiciones libres de plaga y ajustando parámetro de variabilidad temporal del BBF para igualar la variabilidad anual observada de la población de BBF restablecida en la Cuenca de Conata (Livieri 2006; Fig. 6). Aunque la mayor parte de la variabilidad en las poblaciones de BBF probablemente se deba a la variación en la base de presas (aquí traducida en variación en K), la variabilidad en otros factores ambientales puede contribuir a la variabilidad en las tasas vitales del hurón de patas negras. Para estimar la magnitud de esta contribución, creamos un modelo retrospectivo del crecimiento de la población de BBF de la Cuenca de Conata desde 1996 (poco después de su introducción) hasta 2007 (antes del primer brote de peste) basado en Livieri (2006). Reconstruimos el esfuerzo de reintroducción de Conata usando RAMAS Metapop, usando eventos de manejo (introducción y cosecha) para programar la historia de introducciones y traslocaciones de hurones descritas por Livieri (2006). Realizamos las simulaciones con estocasticidad demográfica, tasas vitales especificadas anteriormente y capacidad de carga vinculada a la variabilidad temporal natural en la densidad de población de perritos de la pradera libre de plaga (ver arriba). La variabilidad en el crecimiento de la población de hurones de patas negras en los primeros años del programa de reintroducción de Conata probablemente estuvo relacionada con diferentes estrategias de liberación y medidas de exclusión de depredadores (Livieri 2006). Las liberaciones de BBF terminaron en gran medida en 1999 y, por lo tanto, asumimos que la variabilidad de la población observada desde 2001 hasta 2007 (antes de la epizootia de la peste selvática) se debió principalmente a la variabilidad natural. Manteniendo constantes todas las demás fuentes de variabilidad (estocasticidad demográfica y variabilidad en la abundancia de presas), ajustamos el coeficiente de variación para la variación ambiental en las tasas vitales del hurón de patas negras para que la mediana de la varianza de la población simulada (calculada como la varianza de (Nt + 1 / Nt), n = 1000 simulaciones) coincidió con la variabilidad observada en la serie de tiempo de Conata. El valor de CV que mejor se ajusta a la serie de tiempo de Conata observada (Fig. 6) fue 11,5%, y este valor se utilizó para calcular la variación del proceso temporal para todas las tasas vitales. Para el análisis de sensibilidad, el CV de las tasas vitales de hurones varió entre el 5 y el 16%, que fue el rango de valores de CV para los que la variabilidad observada cayó dentro del rango intercuartílico de las simulaciones.