Capítulo 14 LTRE

library(tidyverse)
library(gt)

por : Adriana Ramírez-Martínez

14.1 Introducción a Experimento de Respuesta de Tabla de Vida

La variación en los estimados de los parámetros de la matriz son inherentes a la biología. Esa variación puede ser a consecuencia de múltiples factores individuales y en combinaciones, incluyendo efectos de tiempo, espacio, genético, tamaño de muestra y suerte (Hernández et al. (2024)) La variación en las parámetros de la historia de vida de una especie y las causas de estas diferencias se puede evaluar a diferentes niveles: genético, demográfico, espacial o temporal. Esta variación en ecología es la norma. La variación se encuentra en todos aspectos desde la parte genética de los individuos que compone una población, la variación ambiental y las interacciones bióticas y abióticas; además de la plasticidad fenotípica que es la interacción entre la genética y el ambiente. ¿Cuál es esa variación? ¿en otra palabra qué es lo que varía? y ¿cómo los individuos responden a las variables bióticas y abióticas? son aspectos importantes para determinar la ecología, evolución y conservación de las especies. La causa de la variación en una población se puede resumir a tres componentes principales, la genética, el efecto del ambiente y la interacción entre ambiente y genética (plasticidad fenotípica) (Hastings et al. (2021); Sun et al. (2019)). Se asume que el tamaño de muestra es suficiente grande para no ser la causa de la variación. Dentro de un contexto de dinámica poblacional las condiciones que los individuos en las poblaciones experimentan varían, ya sea durante tratamientos manipulados, localidades o periodos de tiempo, y por consecuencia los datos que colectamos con diferencias en espacio/tiempo también varían y pudieran tener efecto sobre la matriz de proyección poblacional A. Por tanto, las entradas (los parámetros) de esa matriz A variarán en tiempo/espacio o experimento y esto tendría un impacto sobre la tasa de crecimiento poblacional (λ) y en los estimados de dispersión (Intervalo de confianza o credibilidad; Caswell (2000), Caswell (2010)).

Tomando en cuenta lo anterior un Experimento de Respuesta de Tabla de Vida (ERTV) conocido también como Life Table Response Experiment (LTRE por sus siglas en inglés) descompone la diferencia o varianza en λ entre múltiples poblaciones o tiempo dentro de las contribuciones de los elementos de la matriz y sus interacciones (Caswell (1989)). Entonces al realizar este análisis podemos tener una apreciación de cómo los cambios en la matriz de datos recolectados en diferentes tiempos y espacio impactan las tasas vitales y a su vez que causan cambios en el crecimiento intrínseco λ y otros parámetros poblacionales (Caswell (1989), Caswell (2010)).

Desde la aplicación del primer ERTV por Birch (1953) en su estudio sobre el efecto de la temperatura, humedad y el alimento sobre tres especies de escarabajos de harina, las aplicaciones de estos análisis han sido variadas con diversos fines en las últimas dos décadas (Caswell (1989), Caswell (2010)). Tanto en diseños fijos en los que se manipulan uno o más factores, como en diseños aleatorios en los que se analizan parámetros demográficos en condiciones naturales no manipuladas a lo largo del tiempo o del espacio (Horvitz, Schemske, and Caswell (1997); Teitel, Klimowski, and Campbell (2016)). Los diseños fijos se han utilizado en poblaciones de animales para investigar las consecuencias demográficas de la exposición a contaminantes, la manipulación del alimento o la manipulación de la densidad poblacional (Hansen, Stenseth, and Henttonen (1999), 1999; L. Levin et al. (1996); Oli, Slade, and Dobson (2001)). En plantas, los análisis ERTV se han utilizado para evaluar las consecuencias demográficas de la disponibilidad de polinizadores o de la herbívora, competencia, efectos en intensidades de cosecha y de fenómenos naturales e inducidos por el humano (Davison et al. (2010); Gaoue and Ticktin (2010); Garcı́a and Ehrlén (2002); Hart-Fredeluces, Ticktin, and Lake (2021); Jacquemyn et al. (2012); Miriti, Joseph Wright, and Howe (2001); Mondragón (2009); Nordbakken, Rydgren, and Økland (2004); Schmidt et al. (2011)).

Los métodos para calcular los ERTV están constantemente actualizándose y de acuerdo con (Hernández et al. (2023)) existen 186 análisis de ERTV para 75 especies de animales y 1487 para 200 especies de plantas. Aunque en este trabajo no utilizamos la metodología expuesta por dichos autores mostramos una forma práctica de la aplicación de este análisis.

14.1.1 ¿Cómo se diferencia la elasticidad de ERTV?

A diferencia de la elasticidad, el cual es un tipo de análisis de perturbación que examina cuánto cambiaría el crecimiento de la población si se cambiaran una de las entradas de la matriz comparando múltiples matriz, el análisis ERTV examina cuánto cambió λ en función de la variación observada en las entradas de la matriz (Caswell (2000), Caswell (2010); Horvitz, Schemske, and Caswell (1997)); y por consecuencia es un análisis que toma en cuenta el cambio de las variaciones individualmente registradas en matrices en diferentes poblaciones/ tiempo / experimentos, etc. (Caswell (2010)). Nota que ERTV es una herramienta suplementaria para evaluar el efecto de perturbaciones como los de elasticidad (Caswell (1989)), dinámica de transiciones (Stott, Townley, and Hodgson (2011)) y funciones de transferencias (Stott, Hodgson, and Townley (2012a)) y no un reemplazos. Cada una de estas herramientas tiene un propósito y una interpretación diferente con sus supuestos.

14.2 Métodos

14.2.1 Ejemplo práctico de ERTV

Para ejemplificar el cálculo de los ERTV utilizaremos los datos recabados por Ramírez-Martínez colectados de a 2017-2018 para la orquídea epífita Oncidium brachyandrum Lindl. en un bosque de encino estacional en Oaxaca, México (Ramı́rez Martı́nez et al. (2021)). La pregunta principal del estudio era saber qué tasas vitales estaban ligadas a las variaciones en los valores de λ de poblaciones de O. brachyandrum creciendo sobre dos hospederos Quercus martinezii C.H.Mull. y Q. rugosa Née. Usando el método ERTV se pudo evaluar el efecto que tiene la variación observada en los parámetros de las matrices en función de las especies de hospedero en los que se encontraban creciendo.

Como el ERTV es una forma de análisis retrospectivo y es análogo al ANOVA (porque cuantifica los efectos observados de los elementos individuales de matriz sobre la variación observada en λ, en contraposición a los efectos esperados) se requiere de un valor de referencia para realizar las comparaciones, por lo que se toma la matriz con el valor más alto de λ como valor de referencia (Caswell (2010); Timsina et al. (2021)).

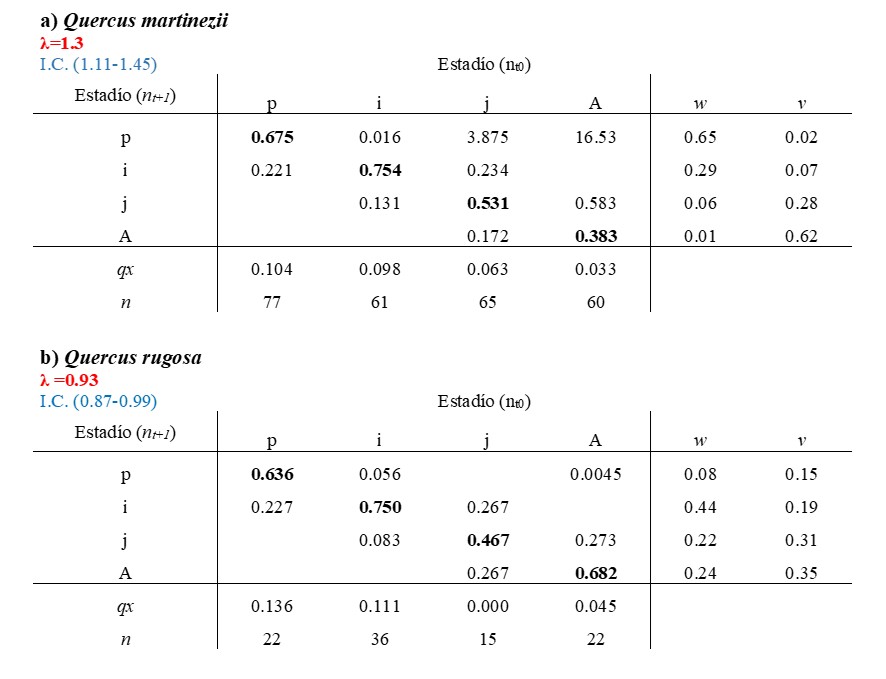
A continuación, se muestran dos matrices de tipo Lefkovitch (matrices construidas a base de estadíos) para las poblaciones de O. brachyandrum y sus valores respectivos de λ en los dos hospederos, Q. martinezii (λ=1.3; I.C: 1.11-1.45) y Q. rugosa (λ=0.98; I.C: 0.87-0.99) (Cuadro 1). Notamos claramente que el valor de λ era mayor en Q. martinezii por lo que la matriz de esta especie fue la matriz de referencia para calcular los ERTV.

14.2.2 Matrices de proyecciones y ciclo de vida por especie de hospedero

Cuadro 1. Matrices de proyección poblaciones de dos poblaciones de Oncidiun brachyandrum creciendo sobre Quercus martinezii y Q. rugosa. Los valores de λ (intervalos de confianza ± 95%) son mostrados en la parte superior izquierda de cada matriz, qx, mortalidad por estadío; w, categorías estables de tamaño por estadío; valor reproductivo por estadío, n = el tamaño de muestra en el tiempo cero (el primer muestreo). p: plántula, i: infantil, j: juvenil, A; adulto (Ramı́rez Martı́nez et al. (2021)). Los valores en negritas son los valores que representan la proporción de individuos que se queda en ese estadio.

14.2.3 Diagrama del ciclo de vida

14.2.4 Diagrama para Quercus martinezii

Primeramente se creó el ciclo de vida por especie de hospedero utilizando el siguiente código:

library(Rage)
library(DiagrammeR)


matmart <- rbind(
  c(0.68, 0.02, 3.88, 16.53),
  c(0.22, 0.76, 0.23, 0.0),
  c(0.0, 0.13, 0.53, 0.58),
  c(0.0, 0.0, 0.17, 0.38))

stages <- c("plántula", "infantil", "juvenil", "adulto") # asignar los nombres de los estadíos
title <- NULL # título del diagrama ninguno
graph <- expand.grid(to = stages, from = stages) # crear un data frame con los estadíos
graph$trans <- round(c(matmart), 4) # redondear los valores de la matriz a 4 decimales
graph <- graph[graph$trans > 0, ] # seleccionar solo los valores mayores a 0
nodes <- paste(paste0("'", stages, "'"), collapse = "; ") # crear los nodos
graph$min_len <- (as.numeric(graph$to) - as.numeric(graph$from)) * 4 # calcular la longitud de las flechas

Figura x: Ciclo de vida de Oncidium brachyandrum creciendo sobre Quercus martinezii. Las flechas representan las transiciones entre estadíos, estasis y fecundidades y los números son las tasas vitales de fecundidad, supervivencia y crecimiento. El color $\color{#ffc125}{\text{amarillo}}$ para fecundidad, $\color{#36648b}{\text{azul}}$ para supervivencia y $\color{#548b54}{\text{verde}}$ para crecimiento, $\color{#7a378b}{\text{violeta}}$ para retroceso y azul oscuro para permanencia.

14.2.5 Diagrama para Quercus rugosa

library(Rage)
library(DiagrammeR)

matrug <- rbind(
  c(0.64, 0.06, 0, 0.0045),
  c(0.27, 0.75, 0.27, 0.0),
  c(0.0, 0.08, 0.47, 0.28),
  c(0.0, 0.0, 0.27, 0.68))
stages <- c("plántula", "infantil", "juvenil", "adulto")
title <- NULL
graph <- expand.grid(to = stages, from = stages)
graph$trans <- round(c(matrug), 4)
graph <- graph[graph$trans > 0, ]
nodes <- paste(paste0("'", stages, "'"), collapse = "; ")
graph$min_len <- (as.numeric(graph$to) - as.numeric(graph$from)) * 4
graph$col <- c(
"steelblue4", "PaleGreen4", "MediumOrchid4", "steelblue4", "PaleGreen4", "MediumOrchid4","steelblue4", "PaleGreen4",  "Goldenrod1", "MediumOrchid4", "steelblue4"
)
edges <- paste0("'", graph$from, "'", " -> ", "'", graph$to, "'",
                "[minlen=", graph$min_len,
                ",fontsize=", 10,
                ",color=", graph$col,
                ",xlabel=", paste("\"", graph$trans),
                "\"]\n",
                collapse = ""
)
grViz(
  paste(
    "
digraph {
  {
    graph[overlap=false];
    rank=same;
    node [shape=", "egg", ", fontsize=", 12, "];",
    nodes, "
  }",
    "ordering=out
  x [style=invis]
  x -> {", nodes, "} [style=invis]", edges,
    "labelloc=\"t\";
  label=\"", title, "\"
}"
  )
)

Figura x: Ciclo de vida de Oncidium brachyandrum creciendo sobre Quercus rugosa. Las flechas representan las transiciones entre estadíos, estasis y fecundidades y los números son las tasas vitales de fecundidad, supervivencia y crecimiento. El color $\color{#ffc125}{\text{amarillo}}$ para fecundidad, $\color{#36648b}{\text{azul}}$ para supervivencia y $\color{#548b54}{\text{verde}}$ para crecimiento, $\color{#7a378b}{\text{violeta}}$ para retroceso y azul oscuro para permanencia.

14.3 Procedimiento para ERTV en Excel

Para facilitar el entendimiento de cómo se calcula ERTV se creó la matriz con los términos de referencia (Cuadro 2).

Cuadro 2. Matriz de términos para el entendimiento de los ERTV. Donde: f= fecundidad, g= crecimiento o retrogresión, p= permanencia y s=supervivencia. Los subíndices se refieren a las transiciones entre estadíos. Nota que los parámetros de juvenil que retrogresan a plántula y y esa etapa produciendo plántulas se suman.

Una vez colocadas las matrices en la hoja de trabajo el primer paso será sumar las columnas para cada estadio, esto significará la supervivencia (s) por estadío (s1, s2, s3, s4); para el caso de Q. martinezii en plántulas sería s1= 0.68+0.22= 0.90 (Figura 3). Después se tienen que calcular las transiciones con respecto a la supervivencia; por lo que para el caso de la transición g12 para la matriz de Q. martinezii tenemos g12= 0.22/0.90=0.25; este cálculo se realiza para todas las transiciones. Los valores de fecundidad (f) se tomarán tal cual de la matriz de fecundidad mat$F. Una vez obtenido esto se procederá a realizar los cálculos con las ecuaciones que se muestran del lado derecho para cada una de las celdas y, además, esto nos sirve para verificar que hayamos calculado bien cada una de las tasas vitales. Por ejemplo, observamos que una proporción de plántulas en Q. martinezii se mantuvo (0.67) este valor se obtiene de multiplicar la supervivencia de plántulas (s1) por la sustracción de 1 menos el crecimiento de plántulas a infantiles 0.89 (1-0.25) = 0.68 (ecuación s1* (1-g12)).

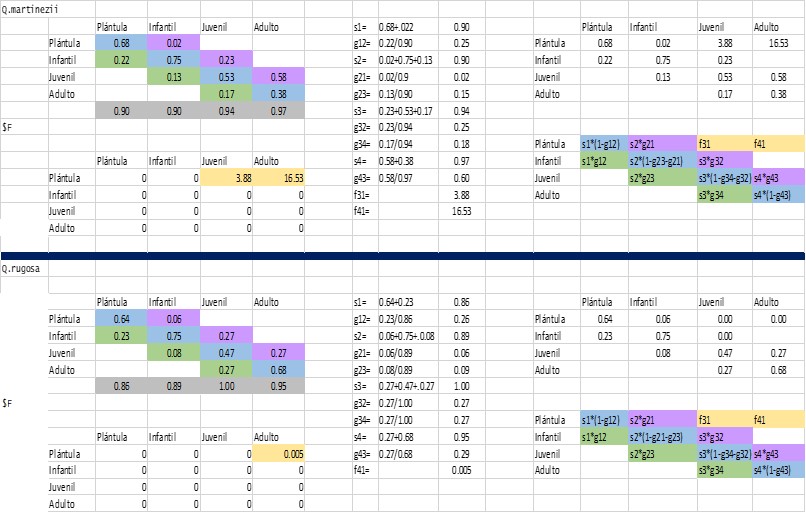
Figura 3. Forma de calcular las ecuaciones para la base de ERTV.

En un archivo nuevo de Excel se arma la base, con la columna de vital rate al principio, seguido por las especies de hospederos (tratamientos) poniendo primeramente el control y después la columna de matrix (Figura 4). Esta base contendrá las ecuaciones de la matriz de referencia. Como la matriz de Q. martinezii tuvo los valores más altos de lambda está ultima de colocará en nuestra base que utilizaremos para correr el análisis ERTV.

names.vitalrate	Martinezzi	Rugosa	matrix
lambda	1.30000	0.9300
s1	0.89610	0.8636	0
g12	0.24630	0.2631	s1*g12
s2	0.90163	0.8888	0
g21	0.01818	0.0625	0
g23	0.14540	0.0937	s2*g21
s3	0.93750	1.0000	2*(1-g23-g21)
g32	0.25000	0.2667	s2*g23
g34	0.18330	0.2667	0
s4	0.96670	0.9545	f31
g43	0.60340	0.2857	s3*g32
f31	3.88000	0.0001	3*(1-g34-g32)
f41	16.53000	0.0045	s3*g34
NA	NA	NA	f41
NA	NA	NA	0
NA	NA	NA	s4*g43
NA	NA	NA	s4*(1-g43)

Figura 4. Ejemplo de base para poder calcular los ERTV.

Es importante colocar en la segunda fila la palabra lambda en la primera columna y después los valores según corresponda a cada tratamiento. Debido a que en Q. rugosa no hubo producción de plántulas (f31) pero en Q. martinezii si hubo se coloca una cantidad muy pequeña pero mayor a cero (e.g. 0.00001) para que se pueda correr el análisis, para las otras transiciones en valor puede ser 0. Una vez culminada la base se guarda el archivo en formato de texto, para continuar en R. Es importante comenzar a colocar las ecuaciones a partir de la segunda fila en la columna matrix.

14.4 Procedimiento en R

Subir la base de datos de la carpeta de trabajo y cargarla en R.

Nota que debería observar la base de datos en la consola de R para verificar que se haya cargado correctamente con los mismos valores que en la hoja de Excel.

# Asegurarse de tener instalado y cargado el paquete 'popbio' package 



library (popbio)

# oncidium<-read.table("data/vitalratesoncidium.txt", sep="\t", header=TRUE, stringsAsFactors=FALSE, fill=TRUE) 
     # Aqui la alternativa si tiene los datos en una hoja de Excel
#oncidium 

Oncidium

## # A tibble: 17 × 4
##    names.vitalrate Martinezzi  Rugosa matrix         
##    <chr>                <dbl>   <dbl> <chr>          
##  1 lambda              1.3     0.93   ""             
##  2 s1                  0.896   0.864  "0"            
##  3 g12                 0.246   0.263  "s1*g12"       
##  4 s2                  0.902   0.889  "0"            
##  5 g21                 0.0182  0.0625 "0"            
##  6 g23                 0.145   0.0937 "s2*g21"       
##  7 s3                  0.938   1      "2*(1-g23-g21)"
##  8 g32                 0.25    0.267  "s2*g23"       
##  9 g34                 0.183   0.267  "0"            
## 10 s4                  0.967   0.954  "f31"          
## 11 g43                 0.603   0.286  "s3*g32"       
## 12 f31                 3.88    0.0001 "3*(1-g34-g32)"
## 13 f41                16.5     0.0045 "s3*g34"       
## 14 <NA>               NA      NA      "f41"          
## 15 <NA>               NA      NA      "0"            
## 16 <NA>               NA      NA      "s4*g43"       
## 17 <NA>               NA      NA      "s4*(1-g43)"

Debido a que la columna de matrix contiene más filas con datos nos aparecerá la leyenda NA en las otras columnas esto se refiere a que no hay valores disponibles para esas filas

Para extraer los nombres de las tasas vitales (de la fila 2 a la 13), sin incluir el valor de λ el cual está en la primera

razonvital<-Oncidium$names.vitalrate[2:13] 

razonvital # mostrar los nombres del objeto razonvital

##  [1] "s1"  "g12" "s2"  "g21" "g23" "s3"  "g32" "g34" "s4"  "g43" "f31" "f41"

14.4.1 Tasa vital sobre Q. martinezzi

Extraer tasas vitales de de la orquídea Oncidium brachyandrum que crecen sobre Q. martinezzi y dejar a lambda a un lado

Martinezzi<-Oncidium$Martinezzi [2:13] # [2:13] se refiere a la fila 2 hasta la 13. 
names(Martinezzi)<-razonvital # asignar los nombres de las tasas vitales
Martinezzi

##       s1      g12       s2      g21      g23       s3      g32      g34 
##  0.89610  0.24630  0.90163  0.01818  0.14540  0.93750  0.25000  0.18330 
##       s4      g43      f31      f41 
##  0.96670  0.60340  3.88000 16.53000

14.4.2 Tasa vital sobre Q. rugosa

Extraer tasas vitales de de la orquidea Oncidium brachyandrum que crecen sobre Q. rugosa y dejar a lambda a un lado

Rugosa<-Oncidium$Rugosa [2:13]
names(Rugosa)<-razonvital # asignar los nombres de las tasas vitales
Rugosa

##     s1    g12     s2    g21    g23     s3    g32    g34     s4    g43    f31 
## 0.8636 0.2631 0.8888 0.0625 0.0937 1.0000 0.2667 0.2667 0.9545 0.2857 0.0001 
##    f41 
## 0.0045

14.4.3 Extraer los elementos de matriz utilizando los nombres de las tasas vitales

matrix.el<-as.expression(parse(text=Oncidium$matrix)) 
matrix.el

## expression(0, s1 * g12, 0, 0, s2 * g21, 2 * (1 - g23 - g21), 
##     s2 * g23, 0, f31, s3 * g32, 3 * (1 - g34 - g32), s3 * g34, 
##     f41, 0, s4 * g43, s4 * (1 - g43))

expression(s1*(1-g12), s1*g12, 0, 0, s2*g21, s2*(1-g23-g21), 
    s2*g23, 0, f31, s3*g32, s3*(1-g34-g32), s3*g34, f41, 0, s4*g43, 
    s4*(1-g43))

## expression(s1 * (1 - g12), s1 * g12, 0, 0, s2 * g21, s2 * (1 - 
##     g23 - g21), s2 * g23, 0, f31, s3 * g32, s3 * (1 - g34 - g32), 
##     s3 * g34, f41, 0, s4 * g43, s4 * (1 - g43))

14.4.4 Calcular las sensibilidades y elasticidades de Onciudium brachyandrum de ambas matrices

Nota que usando la función vitalsens se pueden calcular las sensibilidades y elasticidades de las tasas vitales de las matrices de Oncidium brachyandrum creciendo sobre Q. martinezii y Q. rugosa en un mismo objeto.

14.4.4.1 Quercus matinezzi

14.5 HAY algo extraño en la matriz de sensibilidades y elasticidades, no se ve bien., hay elasticidad negativas, y esto no es posible. Hay que revisar el código.

Martinezzi.se<-vitalsens(matrix.el, Martinezzi)
Martinezzi.se

##     estimate  sensitivity   elasticity
## s1   0.89610  0.120542139  0.052664512
## g12  0.24630  0.438561960  0.052664512
## s2   0.90163  0.166235301  0.073075921
## g21  0.01818 -0.754130522 -0.006684410
## g23  0.14540  0.233443420  0.016548885
## s3   0.93750  0.112464437  0.051405452
## g32  0.25000 -1.371318930 -0.167147994
## g34  0.18330 -1.191967463 -0.106524512
## s4   0.96670  0.047010515  0.022156921
## g43  0.60340  0.014244139  0.004190484
## f31  3.88000  0.019221293  0.036361100
## f41 16.53000  0.001980653  0.015962610

14.5.0.1 Quercus rugosa

Rugosa.se<-vitalsens(matrix.el, Rugosa)
Rugosa.se

##     estimate  sensitivity    elasticity
## s1    0.8636  0.006581052  3.213853e-03
## g12   0.2631  0.021601660  3.213853e-03
## s2    0.8888  0.071964612  3.616938e-02
## g21   0.0625 -1.492714505 -5.275636e-02
## g23   0.0937 -0.960775138 -5.090722e-02
## s3    1.0000  0.071247612  4.028918e-02
## g32   0.2667 -0.361373194 -5.450006e-02
## g34   0.2667 -0.531264040 -8.012195e-02
## s4    0.9545  0.022079896  1.191766e-02
## g43   0.2857  0.033892600  5.475619e-03
## f31   0.0001  0.028076228  1.587658e-06
## f41   0.0045  0.006891115  1.753558e-05

14.5.1 Calcular las diferencias en tasas vitales entre las especies

En esta parte se calculará la diferencia entre las tasas vitales de Oncidium brachyandrum creciendo sobre Q. martinezii y Q. rugosa. ¿Como se interpreta estos resultados?

vr.dif.Martinezzi.Rugosa<-Rugosa-Martinezzi 
vr.dif.Martinezzi.Rugosa

##        s1       g12        s2       g21       g23        s3       g32       g34 
##  -0.03250   0.01680  -0.01283   0.04432  -0.05170   0.06250   0.01670   0.08340 
##        s4       g43       f31       f41 
##  -0.01220  -0.31770  -3.87990 -16.52550

14.5.2 Calcular las tasas vitales para la matriz media

En este paso se calculará la tasa vital media para Oncidium brachyandrum creciendo sobre Q. martinezii y Q. rugosa. La tasa vital media se calcula sumando las tasas vitales de las dos matrices y dividiendo entre 2.

vr.promedia.Martinezzi.Rugosa<-((Rugosa+Martinezzi)/2) #calcular la tazas vitales parta la matrix promedia

# Nota: si se tuvieran 3 matrices se sumarían las tasas vitales de las tres dividido por 3. 

vr.promedia.Martinezzi.Rugosa

##       s1      g12       s2      g21      g23       s3      g32      g34 
## 0.879850 0.254700 0.895215 0.040340 0.119550 0.968750 0.258350 0.225000 
##       s4      g43      f31      f41 
## 0.960600 0.444550 1.940050 8.267250

14.5.3 Calcular las tasas sensibilidades y elasticidades para la matriz media

En este paso se calculará las sensibilidades y elasticidades para la matriz promedia de Oncidium brachyandrum creciendo sobre Q. martinezii y Q. rugosa.

media.sens.Martinezzi.Rugosa<-vitalsens(matrix.el, vr.promedia.Martinezzi.Rugosa) 
media.sens.Martinezzi.Rugosa

##     estimate  sensitivity   elasticity
## s1  0.879850  0.083822341  0.038554963
## g12 0.254700  0.289560608  0.038554963
## s2  0.895215  0.134980693  0.063169999
## g21 0.040340 -0.984263812 -0.020756746
## g23 0.119550 -0.046349418 -0.002896715
## s3  0.968750  0.106300200  0.053834126
## g32 0.258350 -1.022414354 -0.138085243
## g34 0.225000 -0.956257799 -0.112478463
## s4  0.960600  0.050717590  0.025469068
## g43 0.444550  0.022031005  0.005119963
## f31 1.940050  0.022040319  0.022353352
## f41 8.267250  0.003482957  0.015052932

14.5.4 Calcular las contribuciones de ERTV y ver los resultados

LTRE.contrib.Martinezzi.Rugosa<-vr.dif.Martinezzi.Rugosa*media.sens.Martinezzi.Rugosa$sensitivity  
LTRE.contrib.Martinezzi.Rugosa

##            s1           g12            s2           g21           g23 
## -0.0027242261  0.0048646182 -0.0017318023 -0.0436225722  0.0023962649 
##            s3           g32           g34            s4           g43 
##  0.0066437625 -0.0170743197 -0.0797519005 -0.0006187546 -0.0069992504 
##           f31           f41 
## -0.0855142334 -0.0575576132

14.5.5 Resultados de ERTV

LTRE.resultados.Martinezzi.Rugosa<- data.frame(razonvital=razonvital,
                                               rug.vr=Rugosa, 
                                            mart.vr=Martinezzi, 
                                            vr.differencia=vr.dif.Martinezzi.Rugosa, 
                                            media.sens=media.sens.Martinezzi.Rugosa$sensitivity, 
                                            contribucion=LTRE.contrib.Martinezzi.Rugosa)

library(gt)
gt(LTRE.resultados.Martinezzi.Rugosa)

razonvital	rug.vr	mart.vr	vr.differencia	media.sens	contribucion
s1	0.8636	0.89610	-0.03250	0.083822341	-0.0027242261
g12	0.2631	0.24630	0.01680	0.289560608	0.0048646182
s2	0.8888	0.90163	-0.01283	0.134980693	-0.0017318023
g21	0.0625	0.01818	0.04432	-0.984263812	-0.0436225722
g23	0.0937	0.14540	-0.05170	-0.046349418	0.0023962649
s3	1.0000	0.93750	0.06250	0.106300200	0.0066437625
g32	0.2667	0.25000	0.01670	-1.022414354	-0.0170743197
g34	0.2667	0.18330	0.08340	-0.956257799	-0.0797519005
s4	0.9545	0.96670	-0.01220	0.050717590	-0.0006187546
g43	0.2857	0.60340	-0.31770	0.022031005	-0.0069992504
f31	0.0001	3.88000	-3.87990	0.022040319	-0.0855142334
f41	0.0045	16.53000	-16.52550	0.003482957	-0.0575576132

Se puede crear un gráfico de la contribucioón de cada tasa vitales sobre la historia de vida de la especies comparando las dos matrix

ggplot(LTRE.resultados.Martinezzi.Rugosa, aes(y=contribucion, x=razonvital, fill=razonvital))+
  geom_bar(stat="identity")+
  theme_minimal()+
  theme(axis.text.x = element_text(angle = 90, hjust = 1))+
  labs(title="Oncidium vital rate contribución a la diferencia en lambda", x="razonvital", y="contribución")+
  geom_hline(yintercept=0, linetype="dashed", color = "red")+
  xlab("Tasa vitales")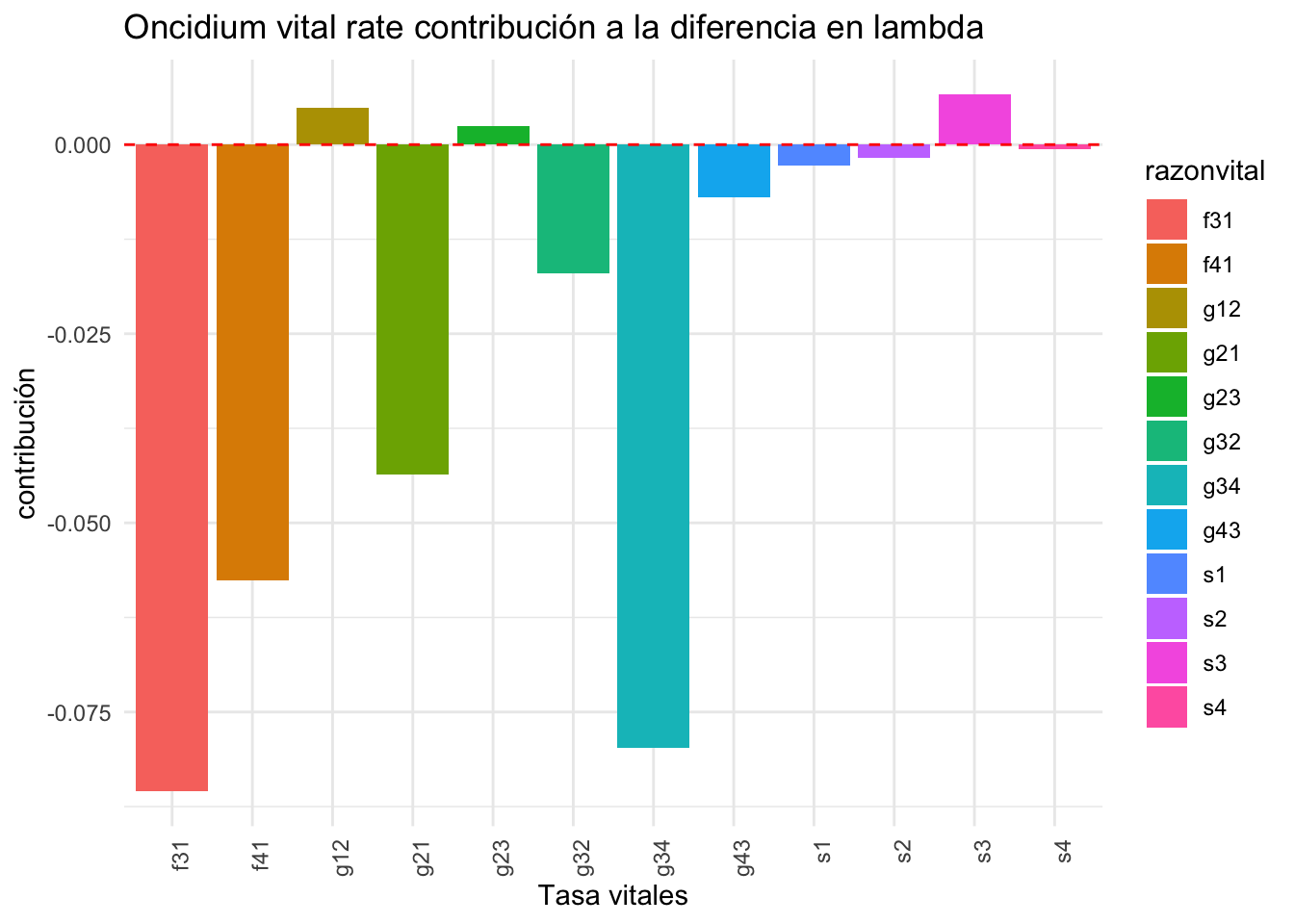

Figure 5. Resultados de un Experimento de Respuesta de la Tabla de Vida (ERTV) llevado a cabo para evaluar las contribuciones de las entradas de la matriz a la variación observada en λ.

De acuerdo con el análisis de elasticidad para cada una de las poblaciones de O. brachyandrum, tanto en Q. martinezii como en Q. rugosa la permanencia de individuos infantiles es la que tiene un mayor impacto sobre los valores de la tasa de crecimiento poblacional (Figura 6). De acuerdo al ERTV, el cual toma en cuenta las diferencias en las tasas vitales y la sensibilidad de lambda que es una función no linear de esas tasas vitales, podemos observar que la fecundidad (fsa) y el crecimiento de plantulas a juveniles (gsj), de juveniles a adultos (gja) y el retroceso de adultos a juveniles (gaj) tiene las mayores contribuciones a las diferencias en lambda entre Q. martinezii y Q. rugosa que la permanencia de plántulas.

Figure 6. Resultados de los análisis de elasticidad, para dos poblaciones de Oncidium brachyandrum creciendo sobre Quercus martinezii y Q. rugosa. Por proceso demográfico (a) y por estadío (b).

ggplot(LTRE.resultados.Martinezzi.Rugosa, aes(y=media.sens, x=razonvital, fill=razonvital))+
  geom_bar(stat="identity")+
  theme_minimal()+
  theme(axis.text.x = element_text(angle = 90, hjust = 1))+
  labs(title="Media Sensitividad ????", x="razonvital", y="contribución")+
  geom_hline(yintercept=0, linetype="dashed", color = "red")+
  xlab("Tasa vitales")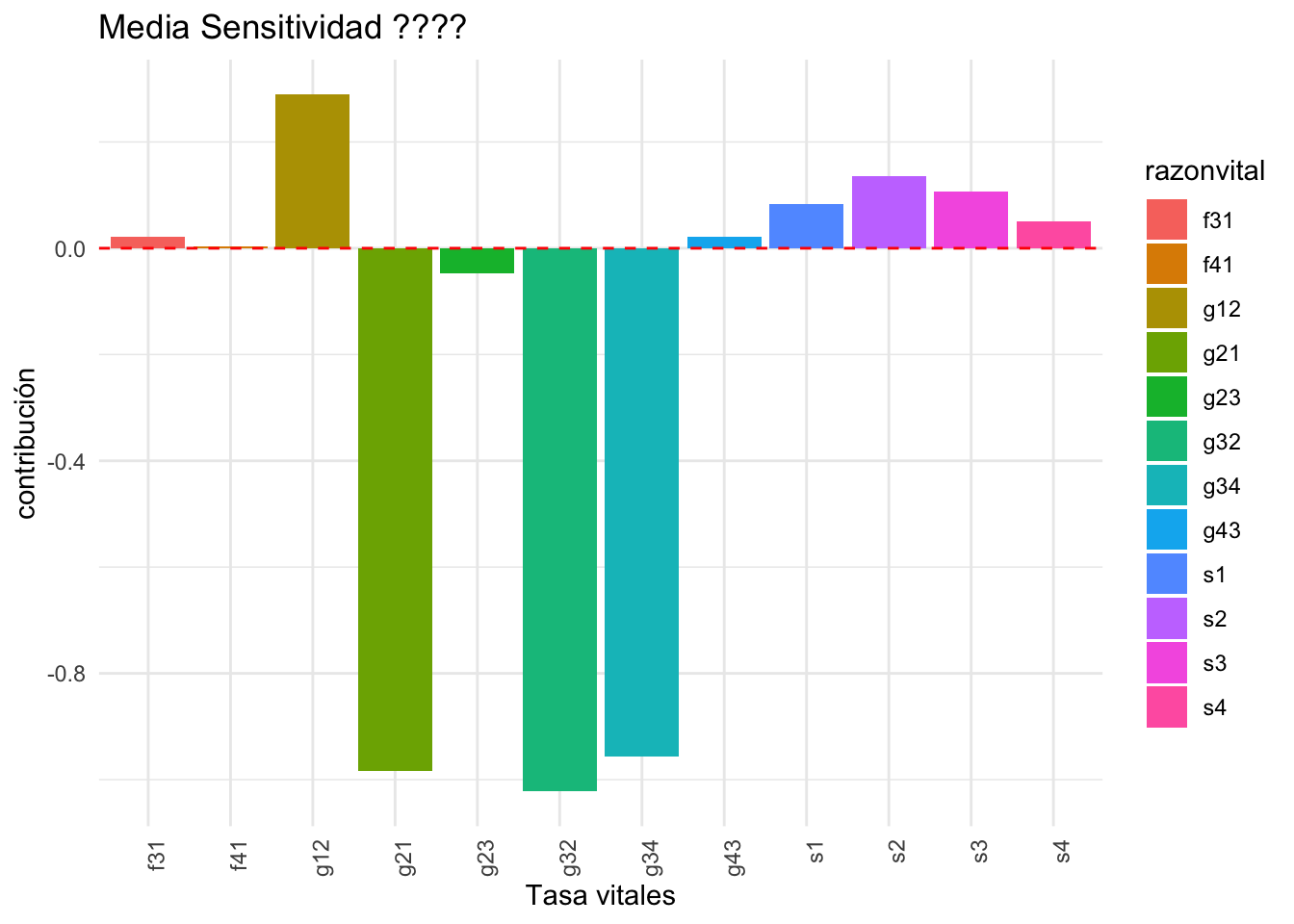

Ahora enseñar como hacer estos análisis sin tener que usar Excel, aquí un set de script para aplicar a Oncidium brachyandrum.

Sugiero que cambie las gráficas a ggplot2 para que se vean más bonitas y consistencia en el libro de herramientas. YO TE AYUDO CON ESTE PASO

AHORA: Si se puede hacer los analisis sin todos los pasos de Excel, se puede hacer directamente en R.

References

Caswell, Hal. 1989. “Analysis of Life Table Response Experiments i. Decomposition of Effects on Population Growth Rate.” Ecological Modelling 46 (3-4): 221–37.

———. 2000. Matrix Population Models. Vol. 1. Sinauer Sunderland, MA.

———. 2010. “Life Table Response Experiment Analysis of the Stochastic Growth Rate.” Journal of Ecology 98 (2): 324–33.

Davison, Raziel, Hans Jacquemyn, Dries Adriaens, Olivier Honnay, Hans De Kroon, and Shripad Tuljapurkar. 2010. “Demographic Effects of Extreme Weather Events on a Short-Lived Calcareous Grassland Species: Stochastic Life Table Response Experiments.” Journal of Ecology 98 (2): 255–67.

Gaoue, Orou G, and Tamara Ticktin. 2010. “Effects of Harvest of Nontimber Forest Products and Ecological Differences Between Sites on the Demography of African Mahogany.” Conservation Biology 24 (2): 605–14.

Garcı́a, Marı́a B, and Johan Ehrlén. 2002. “Reproductive Effort and Herbivory Timing in a Perennial Herb: Fitness Components at the Individual and Population Levels.” American Journal of Botany 89 (8): 1295–1302.

Hansen, Thomas F, Nils C Stenseth, and Heikki Henttonen. 1999. “Multiannual Vole Cycles and Population Regulation During Long Winters: An Analysis of Seasonal Density Dependence.” The American Naturalist 154 (2): 129–39.

Hart-Fredeluces, GM, Tamara Ticktin, and Frank K Lake. 2021. “Simulated Indigenous Fire Stewardship Increases the Population Growth Rate of an Understorey Herb.” Journal of Ecology 109 (3): 1133–47.

Hastings, Alan, Karen C Abbott, Kim Cuddington, Tessa B Francis, Ying-Cheng Lai, Andrew Morozov, Sergei Petrovskii, and Mary Lou Zeeman. 2021. “Effects of Stochasticity on the Length and Behaviour of Ecological Transients.” Journal of the Royal Society Interface 18 (180): 20210257.

Hernández, Christina M, Stephen P Ellner, Peter B Adler, Giles Hooker, and Robin E Snyder. 2023. “An Exact Version of Life Table Response Experiment Analysis, and the r Package exactLTRE.” Methods in Ecology and Evolution 14 (3): 939–51.

Hernández, Christina M, Stephen P Ellner, Robin E Snyder, and Giles Hooker. 2024. “The Natural History of Luck: A Synthesis Study of Structured Population Models.” Ecology Letters 27 (3): e14390.

Horvitz, Carol, Douglas W Schemske, and Hal Caswell. 1997. “The Relative ‘Importance’ of Life-History Stages to Population Growth: Prospective and Retrospective Analyses.” In Structured-Population Models in Marine, Terrestrial, and Freshwater Systems, 247–71. Springer.

Jacquemyn, Hans, Rein Brys, Raziel Davison, Shripad Tuljapurkar, and Eelke Jongejans. 2012. “Stochastic LTRE Analysis of the Effects of Herbivory on the Population Dynamics of a Perennial Grassland Herb.” Oikos 121 (2): 211–18.

Levin, Lisa, Hal Caswell, Todd Bridges, Claudio DiBacco, Debra Cabrera, and Gayle Plaia. 1996. “Demographic Responses of Estuarine Polychaetes to Pollutants: Life Table Response Experiments.” Ecological Applications 6 (4): 1295–1313.

Miriti, Maria N, S Joseph Wright, and Henry F Howe. 2001. “The Effects of Neighbors on the Demography of a Dominant Desert Shrub (Ambrosia Dumosa).” Ecological Monographs 71 (4): 491–509.

Mondragón, Demetria. 2009. “Population Viability Analysis for Guarianthe Aurantiaca, an Ornamental Epiphytic Orchid Harvested in Southeast méxico.” Plant Species Biology 24 (1): 35–41.

Nordbakken, J-F, K Rydgren, and RH Økland. 2004. “Demography and Population Dynamics of Drosera Anglica and d. Rotundifolia.” Journal of Ecology 92 (1): 110–21.

Oli, Madan K, Norman A Slade, and F Stephen Dobson. 2001. “Effect of Density Reduction on Uinta Ground Squirrels: Analysis of Life Table Response Experiments.” Ecology 82 (7): 1921–29.

Ramı́rez Martı́nez, Adriana et al. 2021. “Host Tree Effect on Demography and Phenology of Epiphytic Species.”

Schmidt, Isabel B, Lisa Mandle, Tamara Ticktin, and Orou G Gaoue. 2011. “What Do Matrix Population Models Reveal about the Sustainability of Non-Timber Forest Product Harvest?” Journal of Applied Ecology 48 (4): 815–26.

Stott, Iain, David James Hodgson, and Stuart Townley. 2012a. “Beyond Sensitivity: Nonlinear Perturbation Analysis of Transient Dynamics.” Methods in Ecology and Evolution 3 (4): 673–84.

Stott, Iain, Stuart Townley, and David James Hodgson. 2011. “A Framework for Studying Transient Dynamics of Population Projection Matrix Models.” Ecology Letters 14 (9): 959–70.

Sun, Weihong, Xueyan Yuan, Zhong-Jian Liu, Siren Lan, Wen-chieh Tsai, and Shuang-Quan Zou. 2019. “Multivariate Analysis Reveals Phenotypic Diversity of Euscaphis Japonica Population.” PloS One 14 (7): e0219046.

Teitel, Zachary, Agnieszka Klimowski, and Lesley G Campbell. 2016. “Assessing the Effects of Hybridization and Precipitation on Invasive Weed Demography Using Strength of Selection on Vital Rates.” BMC Evolutionary Biology 16: 1–13.

Timsina, Binu, Pavel Kindlmann, Zuzana Münzbergová, and Maan B Rokaya. 2021. “Six-Year Demographic Study of the Terrestrial Orchid, Crepidium Acuminatum: Implications for Conservation.” Frontiers in Ecology and Evolution 9: 676993.