APPENDIX S1

R code for figures
This appendix provides R code for producing the figures included in the main manuscript.
Install the library using install.packages() or by downloading from http://cran.R-project.org

Load the library

library(popdemo)
library(popbio)
#remotes::install_github("jonesor/Rage")

Lepanthes is one of the largest genera of the Orchidaceae with >1200 species, found only in the Neotropics.

Here is photo of the flower of Lepanthes rubripetala,

Lepanthes rubripetala

A population of Lepanthes rupestris, those of Lepanthes rubripetala growth in the same way (on rocks or trees), so these groups of individuals are discrete and may be seperated by large distances.

Lepanthes population

Articulo para guiar su aprendizaje

Tremblay, Raventos Ackerman. Habrá un quiz de comprobación de lectura al principio de la clase.

Lepanthes rubripetala population #3

How to construct a matrix in R

En general lo que uno hace es separar la matriz de transciones (matU) de la matriz de fecundidad (matF). Eso es para tener claro los procesos que ocurren en la población. Sumando ambas matriz matU+matF = matA tenemos la matriz para evaluar la dinamica poblacional de esa población. Nota que eso es la nueva terminología que van a encontrar en la literatura reciente, matU y matF y matA

library(Rage)
matU=matrix(c(
0.43,   0,      0.00,   0.00, 
0.38,     0.84,   0.00,   0.00, 
0,      0.00,     0.51,   0.15,
0,      0.14,   0.43,   0.84),
byrow=4, ncol=4)

matU

##      [,1] [,2] [,3] [,4]
## [1,] 0.43 0.00 0.00 0.00
## [2,] 0.38 0.84 0.00 0.00
## [3,] 0.00 0.00 0.51 0.15
## [4,] 0.00 0.14 0.43 0.84

matF=matrix(c(
0,    0,      0,    0.14,
0,    0,      0,      0, 
0,    0,      0,      0,    
0,    0,    0,    0
), byrow=4, ncol=4)

matF

##      [,1] [,2] [,3] [,4]
## [1,]    0    0    0 0.14
## [2,]    0    0    0 0.00
## [3,]    0    0    0 0.00
## [4,]    0    0    0 0.00

TF=matU+matF
TF

##      [,1] [,2] [,3] [,4]
## [1,] 0.43 0.00 0.00 0.14
## [2,] 0.38 0.84 0.00 0.00
## [3,] 0.00 0.00 0.51 0.15
## [4,] 0.00 0.14 0.43 0.84

colnames(TF) <- c("plantulas", "juveniles", "A no reprod", "A reprod")
rownames(TF) <- colnames(TF)
TF

##             plantulas juveniles A no reprod A reprod
## plantulas        0.43      0.00        0.00     0.14
## juveniles        0.38      0.84        0.00     0.00
## A no reprod      0.00      0.00        0.51     0.15
## A reprod         0.00      0.14        0.43     0.84

orchid_names= c("1_plantulas", "2_juveniles", "3_adulto no reproductivos", "4_adultos reproductivos")



orchid_names_2= c("1", "2", "3", "4")
#stages <- c(TF_TF) 
plot_life_cycle(TF)

#plot_life_cycle(TF, stages = orchid_names_2)

Here is the theoretical life cycle of the species

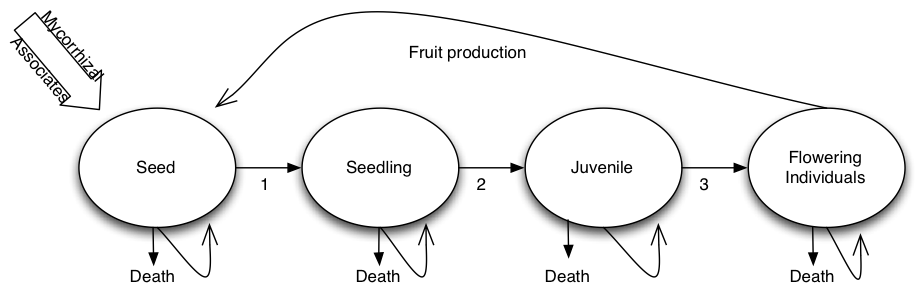
Theoretical life cycle

Crecimiento poblacional intrinsico

La definición de crecimiento poblacional asimptotico”: Si nada más cambia, la población eventualmente alcanza la distribución de etapa estable** y la razón de cambio de la población se acerca a una tasa constante (la tasa de crecimiento demográfico asintótica).

lambda = 1: la población es estable

lambda < 1: la población reduce en tamaño

lambda > 1: la población aumenta

This is a measure of the asymptotic population growth rate of the species

TF

##             plantulas juveniles A no reprod A reprod
## plantulas        0.43      0.00        0.00     0.14
## juveniles        0.38      0.84        0.00     0.00
## A no reprod      0.00      0.00        0.51     0.15
## A reprod         0.00      0.14        0.43     0.84

library(popbio)
lambda(TF) # crecimiento de 3%

## [1] 1.029629

Ejercicio 1

Cambie el valor de supervivencia de los adultos reprodutivos a la mitad y evalue el crecimiento de la población.

library(Rage)
matU1=matrix(c(
0.43,   0,    0,    0.00,
0.38,   0.84,   0,    0, 
0,      0,    0.51, 0.15,   
0,      0.14, 1.43, 0.44
), byrow=4, ncol=4)

matU1

##      [,1] [,2] [,3] [,4]
## [1,] 0.43 0.00 0.00 0.00
## [2,] 0.38 0.84 0.00 0.00
## [3,] 0.00 0.00 0.51 0.15
## [4,] 0.00 0.14 1.43 0.44

matF1=matrix(c(
0,    0,      0,    0.14,
0,    0,      0,      0, 
0,    0,      0,      0,    
0,    0,    0,    0
), byrow=4, ncol=4)

matF1

##      [,1] [,2] [,3] [,4]
## [1,]    0    0    0 0.14
## [2,]    0    0    0 0.00
## [3,]    0    0    0 0.00
## [4,]    0    0    0 0.00

TF1=matU1+matF1
TF1

##      [,1] [,2] [,3] [,4]
## [1,] 0.43 0.00 0.00 0.14
## [2,] 0.38 0.84 0.00 0.00
## [3,] 0.00 0.00 0.51 0.15
## [4,] 0.00 0.14 1.43 0.44

lambda(TF1)

## [1] 0.9846844

Ejercicio 2

Cambie el de reproducción a 100% de la matriz original.

library(Rage)
matU2=matrix(c(
0.43,   0,    0,    0.00,
0.38,   0.84,   0,    0, 
0,      0,    0.51, 0.15,   
0,      0.14, 0.43, 0.84
), byrow=4, ncol=4)

matU2

##      [,1] [,2] [,3] [,4]
## [1,] 0.43 0.00 0.00 0.00
## [2,] 0.38 0.84 0.00 0.00
## [3,] 0.00 0.00 0.51 0.15
## [4,] 0.00 0.14 0.43 0.84

matF2=matrix(c(
0,    0,      0,    3.6,
0,    0,      0,      0, 
0,    0,      0,      0,    
0,    0,    0,    0
), byrow=4, ncol=4)

matF2

##      [,1] [,2] [,3] [,4]
## [1,]    0    0    0  3.6
## [2,]    0    0    0  0.0
## [3,]    0    0    0  0.0
## [4,]    0    0    0  0.0

TF2=matU2+matF2
lambda(TF2)

## [1] 1.339431

x=c(3,4,8,3,3,5,2,7,2,4,2,2,3,3,3)
sum(x)

## [1] 54

mean(x)

## [1] 3.6

Dos posible problemas se tiene que considerar antes de hacer los analisis

Ergodicity
- la condición que irrelevante cual es el la etapa inicial, el crecimiento poblacional asimptotico sera igual
Irreducibility
- la condición que las transiciones de todas las etapas a otra son posibles.

Recuerda la definición de crecimiento poblacional asimptotico”: Si nada más cambia, la población eventualmente alcanza la distribución de etapa estable** y la razón de cambio de la población se acerca a una tasa constante (la tasa de crecimiento demográfico asintótica).

Si no cumple con esas condiciones los analisis pueden ser severamente impactado. (Stott et al., 2010a).

Pueden probar esas dos condiciones usando las funciones en “popdemo”.

library(popdemo)
isErgodic(TF, digits=10, return.eigvec=FALSE)

## [1] TRUE

isIrreducible(TF)

## [1] TRUE

plot_life_cycle(TF)

lambda(TF)

Ergodica

Evaluamos una población que no es Ergodica

Cualquiera que sea la estructura de la etapa inicial que se utilice en la proyección de población, siempre exhibirá la misma tasa de crecimiento asintótica estable.

 library(Rage)
matU4=matrix(c(
0.43,   0,      0,     0.00,
0.38,     0.84,     0,     0, 
0.00,   0,      0.51,    0.15,  
0,      0.0,    0.43,  0.84
), byrow=4, ncol=4)

matU4  # ¿Cual es el problema con esa matriz?

##      [,1] [,2] [,3] [,4]
## [1,] 0.43 0.00 0.00 0.00
## [2,] 0.38 0.84 0.00 0.00
## [3,] 0.00 0.00 0.51 0.15
## [4,] 0.00 0.00 0.43 0.84

matF4=matrix(c(
0,    0,      0,    0.28,
0,    0,      0,      0, 
0,    0,      0,      0,    
0,    0,    0,    0
), byrow=4, ncol=4)

matF4

##      [,1] [,2] [,3] [,4]
## [1,]    0    0    0 0.28
## [2,]    0    0    0 0.00
## [3,]    0    0    0 0.00
## [4,]    0    0    0 0.00

TF4=matU4+matF4

isErgodic(TF4)

## [1] FALSE

isIrreducible(TF4)

## [1] FALSE

plot_life_cycle(TF4)

Irreducible

Evaluamos una población que no es Ergodica

El gráfico del ciclo de vida asociado contiene las tasas de transición necesarias para facilitar los caminos desde todas las etapas a todas las demás etapas

 library(Rage)
matU4=matrix(c(
0.43,   0,    0,    0.00,
0.38,   0.84,   0,    0, 
0,      0,    0.51, 0.15,   
0,      0.0, 0.43, 0.84
), byrow=4, ncol=4)

matU4  # ¿Cual es el problema con esa matriz?

##      [,1] [,2] [,3] [,4]
## [1,] 0.43 0.00 0.00 0.00
## [2,] 0.38 0.84 0.00 0.00
## [3,] 0.00 0.00 0.51 0.15
## [4,] 0.00 0.00 0.43 0.84

matF4=matrix(c(
0,    0,      0,    0.28,
0,    0,      0,      0, 
0,    0,      0,      0,    
0,    0,    0,    0
), byrow=4, ncol=4)

matF4

##      [,1] [,2] [,3] [,4]
## [1,]    0    0    0 0.28
## [2,]    0    0    0 0.00
## [3,]    0    0    0 0.00
## [4,]    0    0    0 0.00

TF4=matU4+matF4

isIrreducible(TF4)

## [1] FALSE

plot_life_cycle(TF4)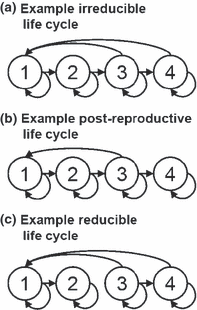

Irreducible Matrix

Realidad de la recopilación de datos

Sin embargo, los datos de la siguiente matriz son limitados porque la colonización de semillas no se puede detectar en el campo con facilidad, porque las semillas son demasiado pequeñas y no existe una técnica rápida en el campo para detectar los hongos simbióticos y la colonización de los hongos entrando en la semilla.

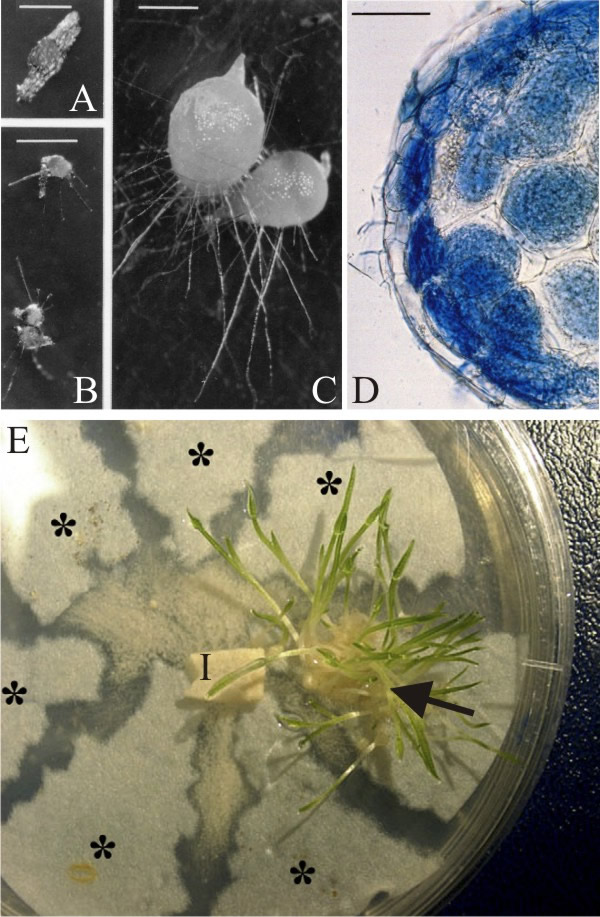
Orchid with Mycorrhiza: From 21st Century Guidebook to Fungi, SECOND EDITION, by David Moore, Geoffrey D. Robson and Anthony P. J. Trinci

Esta matriz se basa en el tamaños o carateristicas observable en el campo, con una fecundidad media. Las clases de tamaño son las siguientes:

1: Plántula
2: Juveniles
3: A0: adultos no reproductivos
4: A+: adultos reproductivos

#FIGURE 1: POPULATION PROJECTION #

#This figure is designed to be 3.5” by 3.5” #(Check size of plot window using ‘par(din)’). # # #Set margins: par(mar=c(5,4,1,1))

#Create a population vector. This one is biased towards adults.

n0 <- c(10, 10, 10, 10)

Now project the population for x years in the future.

Project the orchid PPM and population vector. In this case, we are projecting for 24 time intervals. The orchid interval is one month, so this projection is for 2 years. We use the function ‘project’.

pr1 <- project(TF, vector=n0, time=24)

#Plot the projection. This uses an S3 plotting
#method for projections. For info, see '?plot.projection'.  
plot(pr1)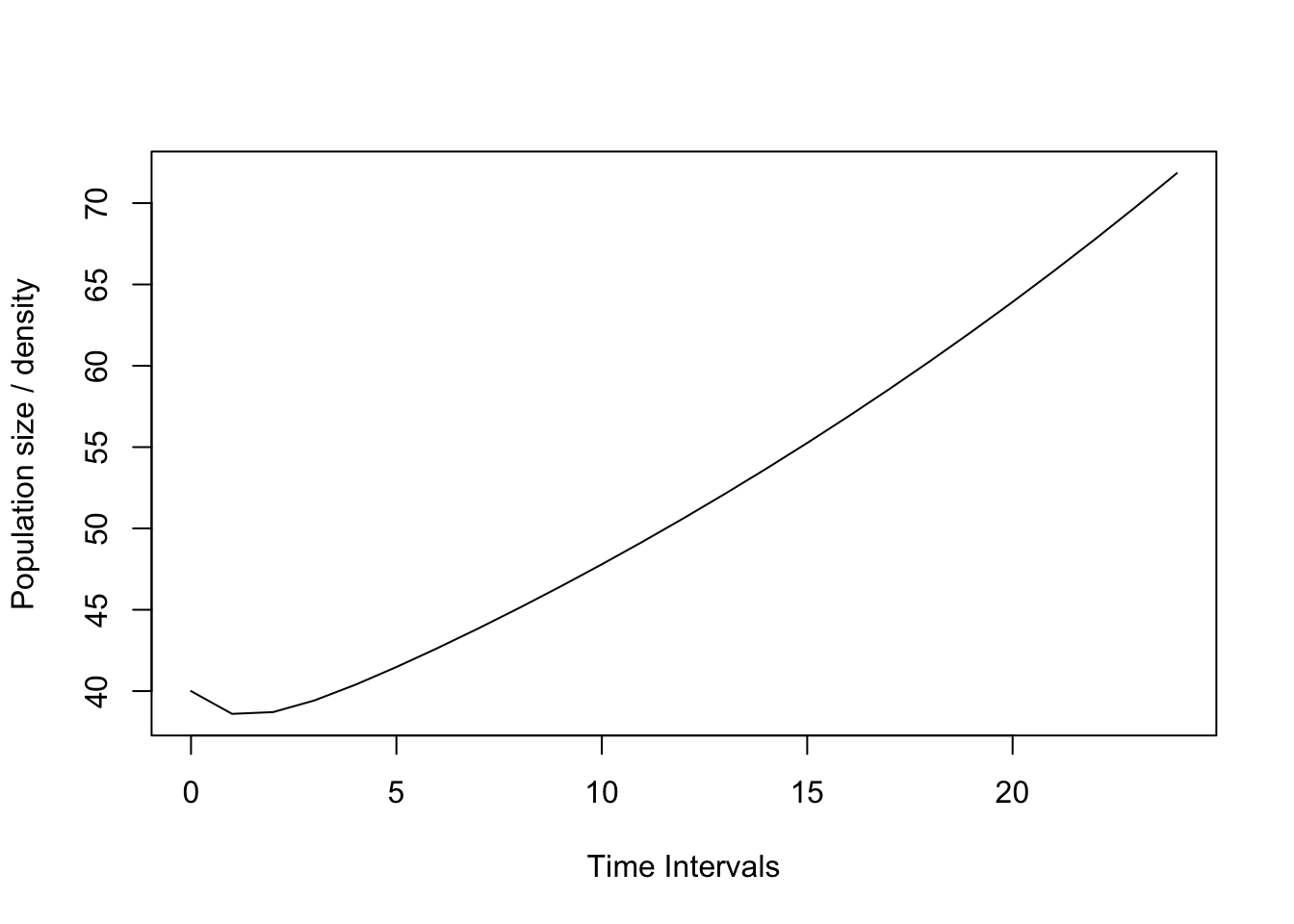

Primitive Matrix

For a primitive matrix (see below), the long-term growth rate is the real part of the first dominant eigenvalue of the PPM.

eigs <- eigen(TF)
eigs # los diferentes eigenvalue de la matrix. El que responde al crecimiento intrinsico de la población es la parte mayor real.

## eigen() decomposition
## $values
## [1] 1.0296288+0.00000000i 0.7709252+0.00000000i 0.4097230+0.05003503i
## [4] 0.4097230-0.05003503i
## 
## $vectors
##              [,1]          [,2]                    [,3]                    [,4]
## [1,] 0.2004457+0i -0.1598129+0i  0.67656050+0.00000000i  0.67656050+0.00000000i
## [2,] 0.4016762+0i  0.8791759+0i -0.58953389-0.06855432i -0.58953389+0.06855432i
## [3,] 0.2478274+0i -0.2237269+0i  0.26185876-0.23103598i  0.26185876+0.23103598i
## [4,] 0.8585216+0i -0.3891732+0i -0.09799012+0.24179804i -0.09799012-0.24179804i

lambdamax <- Re(eigs$values[1]) # esta función seleciona para el primer valor
lambdamax

## [1] 1.029629

# Es más facil utilzar la siguiente función en el paquete popdemo

truelambda(TF) # Con el paquete popdemo

##          [,1]     [,2]
## [1,] 1.029629 1.029629
## [2,] 1.029629 1.029629
## [3,] 1.029629 1.029629
## [4,] 1.029629 1.029629

popbio::lambda(TF) # con el paquete popbio

## [1] 1.029629

Distribución estable de la población, w

Stable Stage distribution

The stable demographic structure of the population is equal to the dominant right eigenvector, which is the absolute value of the real part of the first eigenvector.

This is the expected proportional distribution among the different stages IF the population attains a stable structure.

Compara la porporción que hay por etapas al principio de la investigación.

n0 <- c(10, 10, 10, 10)

library(popbio)
w <- stable.stage(TF)
w

##   plantulas   juveniles A no reprod    A reprod 
##   0.1173246   0.2351086   0.1450580   0.5025088

barplot(w, col="green", ylim=c(0,1), las=1, main="Lepanthes rubripetala",
     ylab="La proporción Etapa de Vida", xlab="Etapas de vida")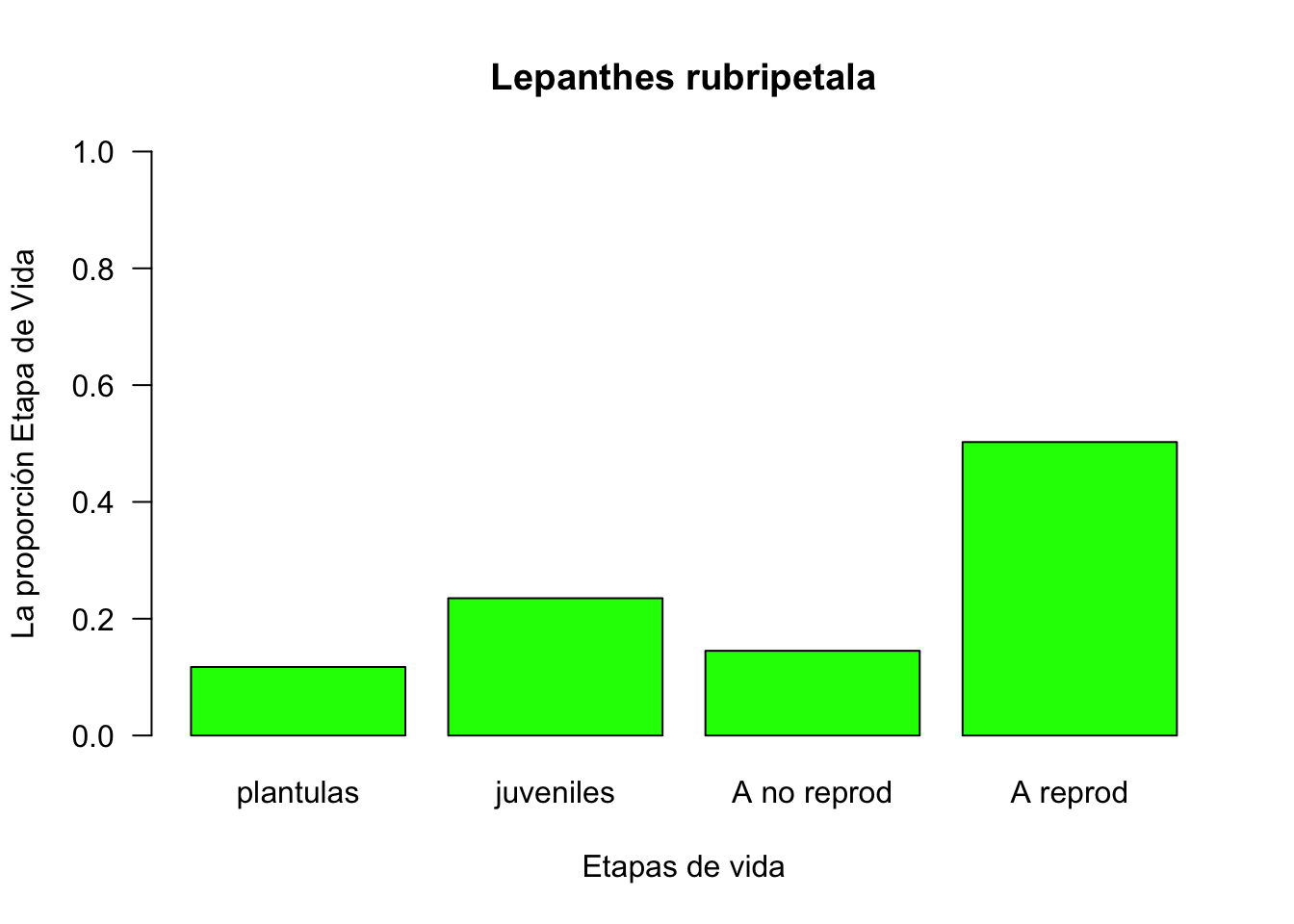

Note that the package popbio provides functions ‘lambda’ and ‘stable.stage’ that will provide these also.

Elasticidad

• Elasticity: the proportional change in population growth rate resulting from an equivalent proportional change in a specific vital rate.

• Elasticidad: el cambio proporcional en la tasa de crecimiento de la población resultante de un cambio proporcional equivalente en una tasa vital específica.

elas(TF)

##              plantulas  juveniles A no reprod   A reprod
## plantulas   0.02693792 0.00000000  0.00000000 0.03756455
## juveniles   0.03756455 0.16639992  0.00000000 0.00000000
## A no reprod 0.00000000 0.00000000  0.06986646 0.07118554
## A reprod    0.00000000 0.03756455  0.07118554 0.48173098

Excercise. Caretta caretta

Use data from COMADRE: Crowder LB; Crouse DT; Heppell SS; Martin Reference Type: Journal Article DOI/ISBN: 10.2307/1941948 Journal Name: Ecol Appl Title: Year: 1994 Volume: Pages:

Caretta caretta:

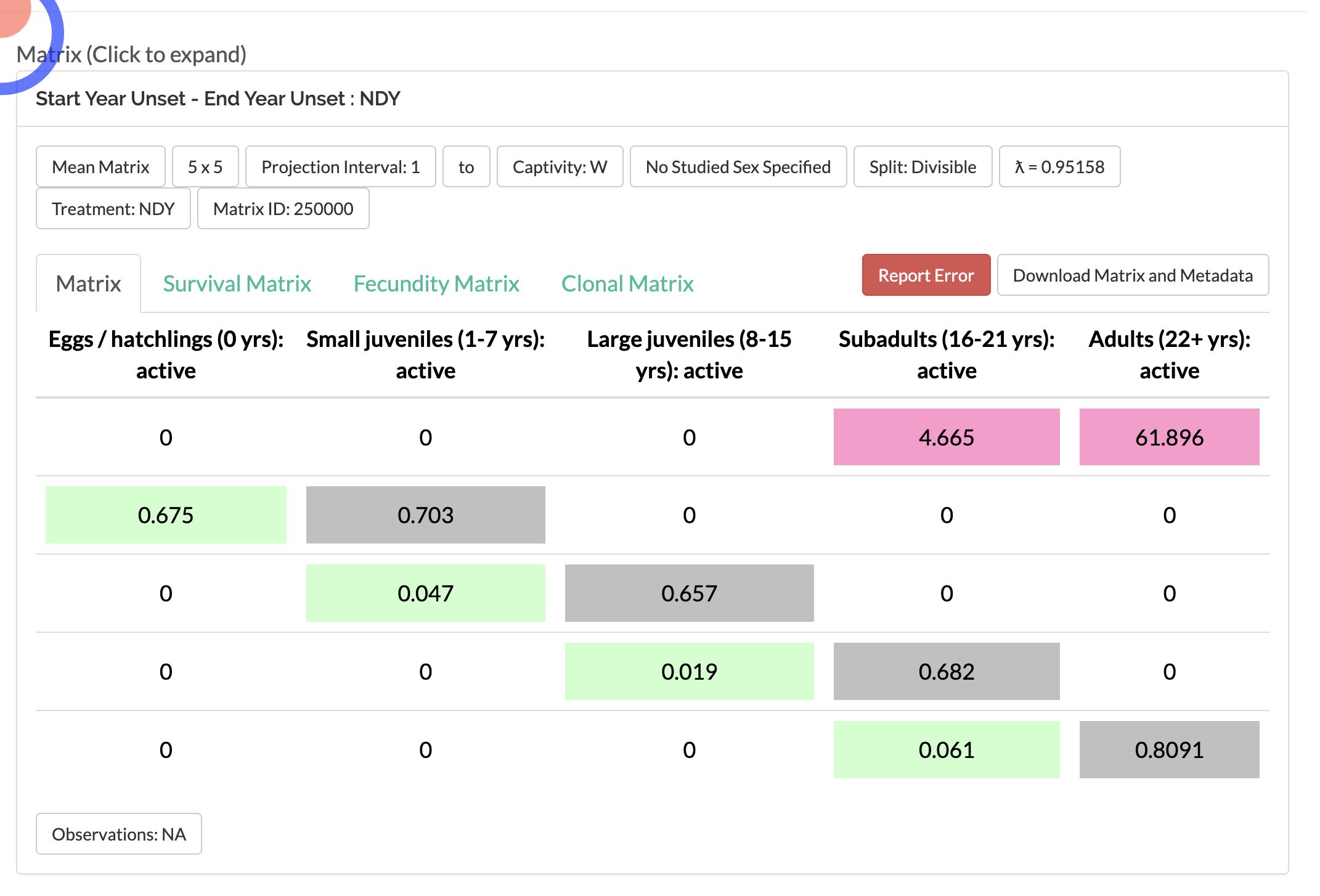
Caretta caretta matrix

#remotes::install_github("jonesor/Rage") # eso es para instalar el programa directo de github

Las matrices

matUCc=matrix(c(
0,      0,           0,     0,     0,
0.675,  0.703,     0,       0,     0,
0,      0.047,     0.657,  0,    0, 
0   ,     0,           0.019,   0.682, 0,
0,      0,         0,     0.061, 0.8091
), byrow=5, ncol=5)



matFCc=matrix(c(            
0,  0,  0,  4.665, 61.896,
0,  0,  0,  0, 0,
0,  0,  0,  0, 0,
0,  0,  0,  0, 0,
0,  0,  0,  0, 0
), byrow=5, ncol=5)

matACc=matUCc+matFCc

matACc

##       [,1]  [,2]  [,3]  [,4]    [,5]
## [1,] 0.000 0.000 0.000 4.665 61.8960
## [2,] 0.675 0.703 0.000 0.000  0.0000
## [3,] 0.000 0.047 0.657 0.000  0.0000
## [4,] 0.000 0.000 0.019 0.682  0.0000
## [5,] 0.000 0.000 0.000 0.061  0.8091

plot_life_cycle(matACc)

colnames(matACc) <- c("Huevos", "small_juv(1-7yrs)", "Large_juv(8-15)", "Subadults(16-21)", "Adults(22+)")
rownames(matACc) <- colnames(matACc)


library(Rage)
plot_life_cycle(matACc) # life cycle with names

truelambda(matACc)

##           [,1]      [,2]
## [1,] 0.9515816 0.9515817
## [2,] 0.9515816 0.9515817
## [3,] 0.9515816 0.9515818
## [4,] 0.9515817 0.9515818
## [5,] 0.9515817 0.9515819

lambda(matACc)

## [1] 0.9515817

Plot turtle growth

nCc <- c(10, 10, 10, 10, 1000)
pr1 <- project(matACc, vector=nCc, time=240)

#Plot the projection. This uses an S3 plotting
#method for projections. For info, see '?plot.projection'.  
plot(pr1)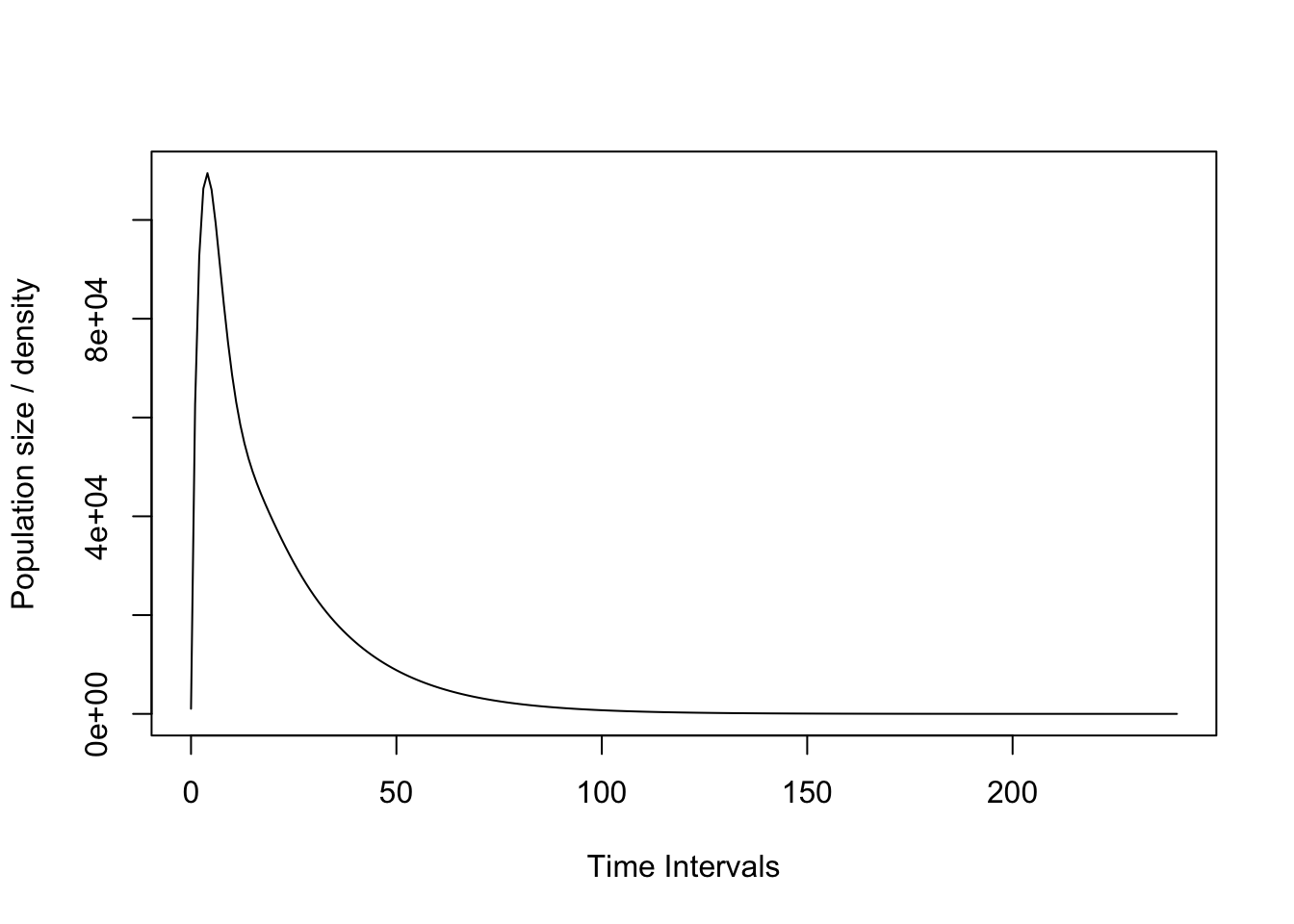

Elasticities

Perturbation analysis is an intuitively appealing way to answer questions about the relative importance of variation in parameters in the matrix. … Elasticity analysis estimates the effect of a proportional change in the vital rates on population growth rate λ (= er, where r is the per capita rate of population increase)1, 2.

matACc # the matrix matU

##                   Huevos small_juv(1-7yrs) Large_juv(8-15) Subadults(16-21)
## Huevos             0.000             0.000           0.000            4.665
## small_juv(1-7yrs)  0.675             0.703           0.000            0.000
## Large_juv(8-15)    0.000             0.047           0.657            0.000
## Subadults(16-21)   0.000             0.000           0.019            0.682
## Adults(22+)        0.000             0.000           0.000            0.061
##                   Adults(22+)
## Huevos                61.8960
## small_juv(1-7yrs)      0.0000
## Large_juv(8-15)        0.0000
## Subadults(16-21)       0.0000
## Adults(22+)            0.8091

round(elas(matACc),digit=4) # elas=elasticities, en el paquete "popdemo"

##                   Huevos small_juv(1-7yrs) Large_juv(8-15) Subadults(16-21)
## Huevos            0.0000            0.0000          0.0000           0.0087
## small_juv(1-7yrs) 0.0579            0.1638          0.0000           0.0000
## Large_juv(8-15)   0.0000            0.0579          0.1292           0.0000
## Subadults(16-21)  0.0000            0.0000          0.0579           0.1465
## Adults(22+)       0.0000            0.0000          0.0000           0.0492
##                   Adults(22+)
## Huevos                 0.0492
## small_juv(1-7yrs)      0.0000
## Large_juv(8-15)        0.0000
## Subadults(16-21)       0.0000
## Adults(22+)            0.2796

Stable Stage distribution.

La proporción de individuos por etapa cuando la población llega a su estabilidad/madura

stable.stage(matACc) # en el paquete popdemo

##            Huevos small_juv(1-7yrs)   Large_juv(8-15)  Subadults(16-21) 
##       0.238535412       0.647720163       0.103342617       0.007283541 
##       Adults(22+) 
##       0.003118266

Damping Ratio

Es un indice de medida de tiempo que toma la población a llegar a su etapas estable

\[\rho=\frac{\lambda_1}{|\lambda_2|}\]

The damping ratio (ρ) is a measure of how fast a population will converge to the stable stage distribution and is defined as the dominant eigenvalue (λ1) divided by the absolute value of the largest subdominant eigenvalue (λ2) (Caswell 1989).

Thus small damping ratio suggest that populations will take a long time to attain stable stage distribution, while large damping ratio, the stable stage distribution will be attain within a few time periods.

eigen(TF)

## eigen() decomposition
## $values
## [1] 1.0296288+0.00000000i 0.7709252+0.00000000i 0.4097230+0.05003503i
## [4] 0.4097230-0.05003503i
## 
## $vectors
##              [,1]          [,2]                    [,3]                    [,4]
## [1,] 0.2004457+0i -0.1598129+0i  0.67656050+0.00000000i  0.67656050+0.00000000i
## [2,] 0.4016762+0i  0.8791759+0i -0.58953389-0.06855432i -0.58953389+0.06855432i
## [3,] 0.2478274+0i -0.2237269+0i  0.26185876-0.23103598i  0.26185876+0.23103598i
## [4,] 0.8585216+0i -0.3891732+0i -0.09799012+0.24179804i -0.09799012-0.24179804i

# Calcular a mano el damping.ratio
1.0296/abs(0.7709) # Calcular a mano

## [1] 1.335582

dr(TF, return.time=TRUE, x=10)

## $dr
## [1] 1.335576
## 
## $t
## [1] 7.957447

eigen(matACc)

## eigen() decomposition
## $values
## [1] 9.515817e-01+0.0000000i 7.116992e-01+0.2231612i 7.116992e-01-0.2231612i
## [4] 4.761170e-01+0.0000000i 2.880582e-06+0.0000000i
## 
## $vectors
##                [,1]                       [,2]                       [,3]
## [1,] 0.341748635+0i -0.0120093429-0.308076711i -0.0120093429+0.308076711i
## [2,] 0.927985828+0i -0.9318454510+0.000000000i -0.9318454510+0.000000000i
## [3,] 0.148058513+0i -0.0453781577+0.185133353i -0.0453781577-0.185133353i
## [4,] 0.010435098+0i  0.0149827612+0.005857473i  0.0149827612-0.005857473i
## [5,] 0.004467527+0i -0.0001565665-0.004027127i -0.0001565665+0.004027127i
##                 [,4]            [,5]
## [1,] -0.309283738+0i -0.720439943+0i
## [2,]  0.920150536+0i  0.691748157+0i
## [3,] -0.239088653+0i -0.049486006+0i
## [4,]  0.022064397+0i  0.001378648+0i
## [5,] -0.004042033+0i -0.000103940+0i

matACc

##                   Huevos small_juv(1-7yrs) Large_juv(8-15) Subadults(16-21)
## Huevos             0.000             0.000           0.000            4.665
## small_juv(1-7yrs)  0.675             0.703           0.000            0.000
## Large_juv(8-15)    0.000             0.047           0.657            0.000
## Subadults(16-21)   0.000             0.000           0.019            0.682
## Adults(22+)        0.000             0.000           0.000            0.061
##                   Adults(22+)
## Huevos                61.8960
## small_juv(1-7yrs)      0.0000
## Large_juv(8-15)        0.0000
## Subadults(16-21)       0.0000
## Adults(22+)            0.8091

0.95158/abs(0.711699)

## [1] 1.337054

dr(matACc)

## [1] 1.275807

dr(matACc, return.time=TRUE, x=10) # damping ratio

## $dr
## [1] 1.275807
## 
## $t
## [1] 9.453131

Convergence Time

Convergence Time is the expected time for a population at attain stable stage distribution. Calculate the time to convergence of a population matrix projection model from the model projection. convt(A, vector = “n”, accuracy = 0.01, iterations = 1e+05)

# convt, en popdemo
n=c(1000,0,0,0, 0)
convt(matACc, accuracy=1e-3, vector=n) # Convergence time to Stable Stage Distribution from an invasive species starting with smallest size

## [1] 27

n1=c(238,648,103,7, 3)
convt(matACc, accuracy=1e-3, vector=n1) # Convergence time to Stable Stage Distribution when close to Stable Stage

## [1] 6

n2=c(0,0,0,0,1000)
convt(matACc, accuracy=1e-3, vector=n2) # Convergence time to Stable Stage Distribution when starting with an invasive species of adults

## [1] 24

TRANSIENT DYNAMICS

Fig. 2a: Population-specific transient dynamics # This figure is designed to be 3.5” by 3.5” (Check size of plot window using ‘par(din)’).

Set margins:

par(mar=c(10,4,1,1))

Create 2 population vectors. One is adult- biased, and it amplifies. One is juvenile- biased and it attenuates.

n0.att <- c(1000,1,1,1) # La población es sesgada a una estructura de etapas pequeñas

n0.amp <- c(1,1,1,1000) # la población es sesgada a una estructura de etapas grandes

Project these vectors using the project function. We are standardising the matrix using ‘standard.A=T’ to remove effects of asymptotic dynamics. This means that the projection has a long-term growth rate of unity, i.e. it does not grow or decline in the long-term. We also standardise the population vector to sum to 1 using ‘standard.vec=T’. These standardisations make it easier (and fairer) to compare between models with different population sizes, and different long-term growth rates.

pr2.1amp <- project(TF, vector=n0.amp, time=50, 
                 standard.A=T, standard.vec=T)
pr2.2att <- project(TF, vector=n0.att, time=50, 
                 standard.A=T, standard.vec=T)

Plot the amplification projection and label it

plot(pr2.2att, ylim=c(0.4,1.0), log="y", cex.axis=0.8)
text(30, pr2.2att[10], "attenuation", 
     adj=c(1,-0.5), cex=0.8)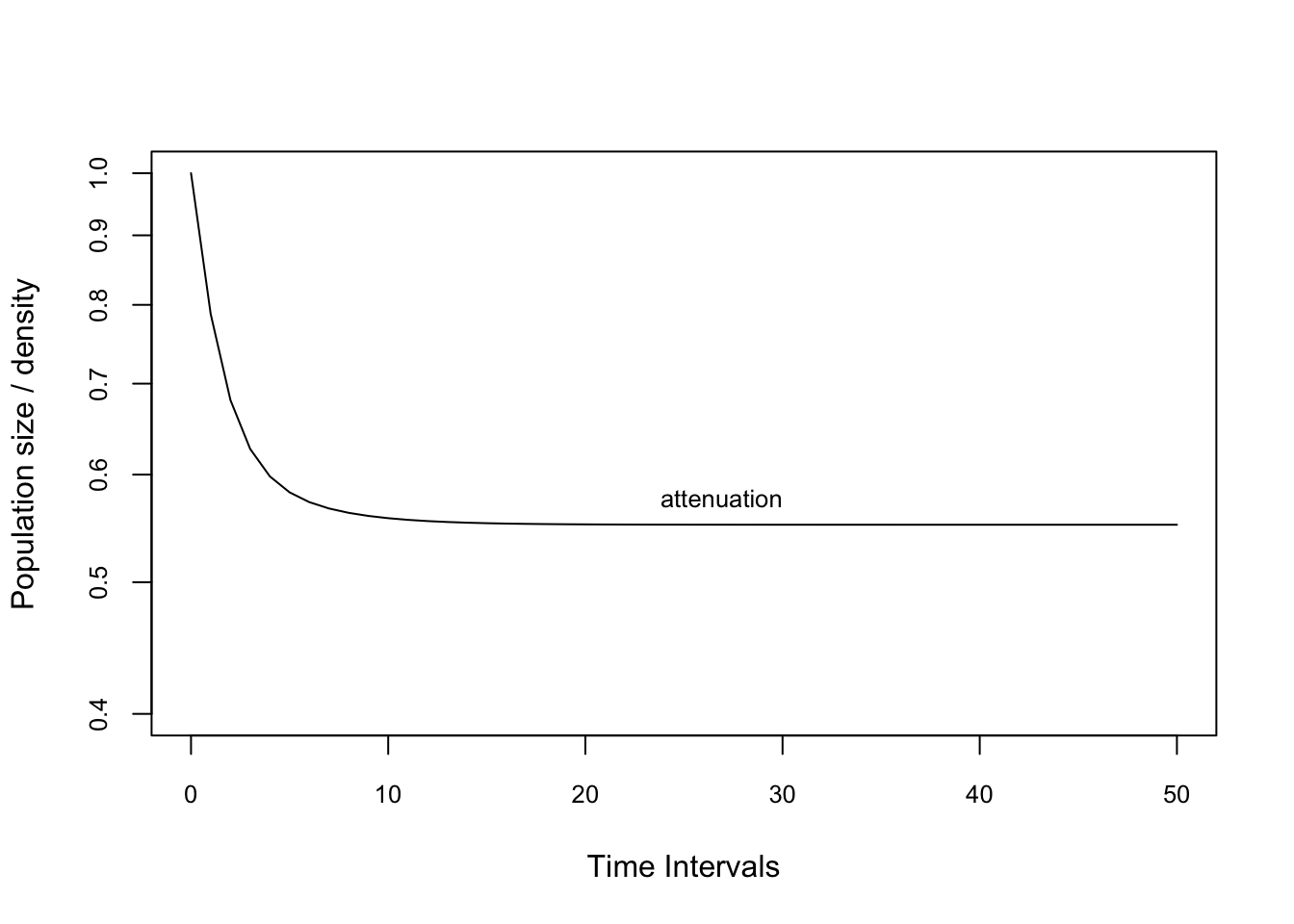

plot(pr2.1amp, ylim=c(0.4,1.2), log="y", cex.axis=0.8)
text(30, pr2.1amp[10], "amplification", 
     adj=c(1,-.25), cex=0.8)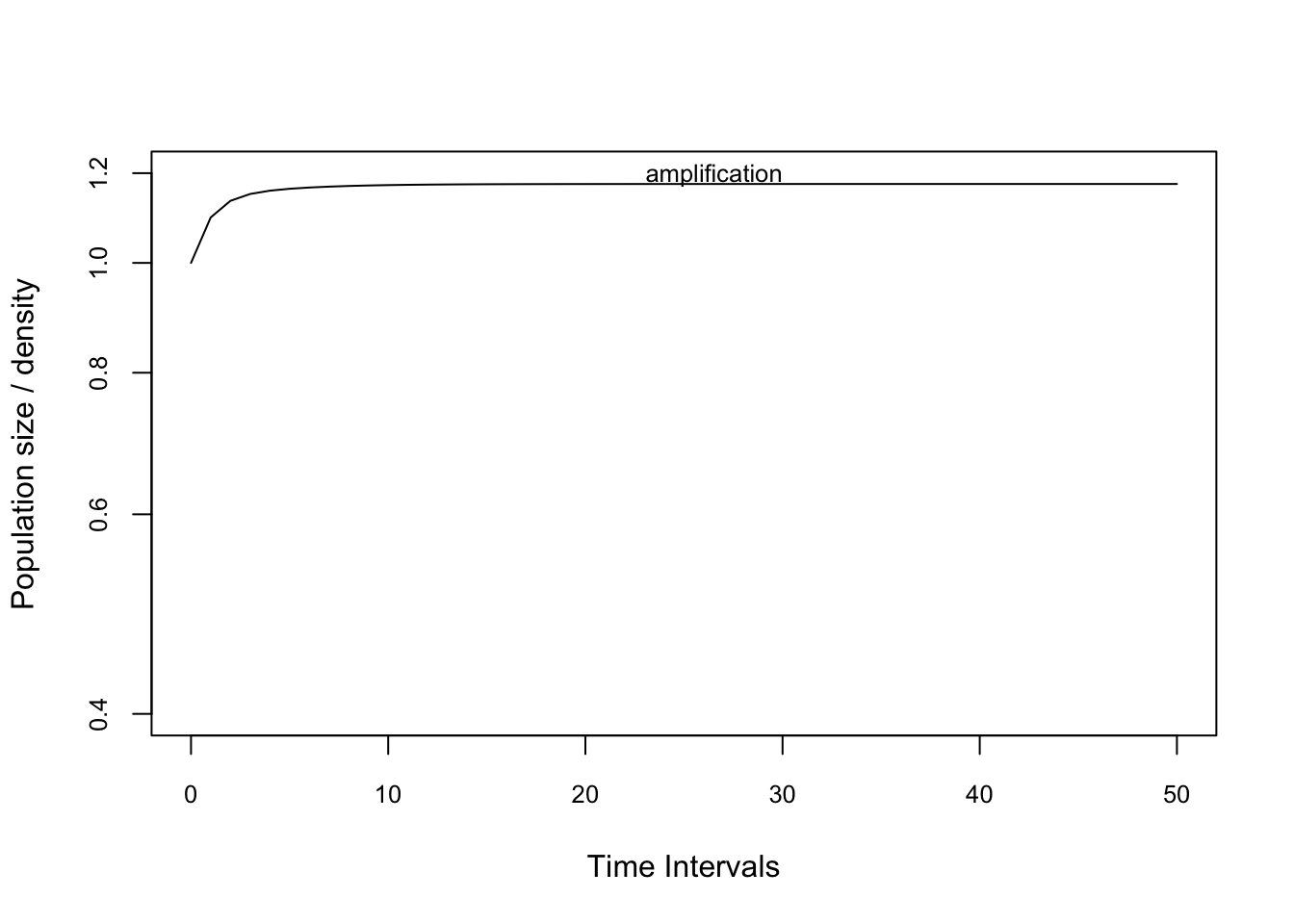

maxamp(TF )

## [1] 1.17506

reac(TF,bound = "upper")

## [1] 1.097483

inertia(TF,bound = "lower")

## [1] 0.5497777

Calculate the transient dynamics of the amplification projection.

reac <- reac(TF, vector=n0.amp)
maxamp <- maxamp(TF,  return.t=T)
upinertia <- inertia(TF, vector=n0.amp)

Add points on the projection for amplification and label them

par(mar=c(10,4,1,1))
points(c(1,maxamp$t,31), c(reac,maxamp$maxamp,upinertia), 
       pch=3, col="red")
text(1, reac, expression(bar(P)[1]), 
     adj=c(-0.3,0.5), col="red", cex=0.8)
text(maxamp$t, maxamp$maxamp, expression(bar(P)[max]), 
     adj=c(0.1,-0.5), col="red", cex=0.8)
text(31, upinertia, expression(bar(P)[infinity]), 
     adj=c(0.1,-0.5), col="red", cex=0.8)

#Add in the second projection using the
#'lines' command and label it
lines(0:50, pr2.2)
text(52, pr2.2[51], "attenuation", adj=c(1,1), cex=0.8)

Calculate the transient dynamics of the attenuation projection firstep <- firststepatt(TF, vector=n0.att) maxatt <- maxatt(TF, vector=n0.att, return.t=T) lowinertia <- inertia(TF, vector=n0.att)

firststepatt(TF, vector=n0.att) maxatt(TF, vector=n0.att, return.t=T) inertia(TF, vector=n0.att)

Add points on the attenuation projection and label them points(c(1,maxatt$t,31), c(firstep,maxatt$maxatt,lowinertia), pch=3, col=“red”) text(1, firstep, expression(underline(P)[1]), adj=c(0,-0.6), col=“red”, cex=0.8) text(maxatt$t, maxatt$maxatt, expression(underline(P)[min]), adj=c(0.1,1.5), col=“red”, cex=0.8) text(31, lowinertia, expression(underline(P)[infinity]), adj=c(0.1,1.5), col=“red”, cex=0.8)

Add in a dotted line at y=1 lines(c(0,50),c(1,1),lty=2)

Fig. 2b: Transient bounds This figure is designed to be 3.5” by 3.5” (Check size of plot window using ‘par(din)’).

Set margins: par(mar=c(5,4,1,1))

Transient bounds result from projections of the stage-biased dynamics of the model. When using the function ‘project’, the stage-biased model dynamics are projected automatically if no population vector is specified. We can do this for the orchid, using a standardised matrix like before: pr2 <- project(TF, standard.A=TRUE, time=156)

Now we need to plot these population dynamics. The S3 method for projections automatically plots all stage-biased projections: plot(pr2, log=“y”, cex.axis=0.8, ylim=c(0.4,1.5))

Add in a dotted line at y=1 lines(c(0,156), c(1,1), lty=2)

Calculate the bounds on transient dynamics for the orchid. This is also done automatically if no population vector is specified. reacb <- reactivity(TF) firstepb <- firststepatt(TF) maxampb <- maxamp(TF, return.t=T) maxattb <- maxatt(TF, return.t=T) upinertiab <- inertia(TF, bound=“upper”) lowinertiab <- inertia(TF, bound=“lower”)

reactivity(TF) firststepatt(TF) maxamp(TF, return.t=T) maxatt(TF, return.t=T) inertia(TF, bound=“upper”) inertia(TF, bound=“lower”)

Add points on the projection and label them points(c(1,1,maxampb$t,maxattb$t,31,31), c(reacb,firstepb,maxampb$maxamp,maxattb$maxatt,upinertiab,lowinertiab), pch=3,col=“red”) text(1, reacb, expression(bar(rho)[1]), adj=c(-0.5,0.5), col=“red”, cex=0.8) text(1, firstepb, expression(underline(rho)[1]), adj=c(-0.5,1.5), col=“red”, cex=0.8) text(maxampb$t, maxampb$maxamp, expression(bar(rho)[max]), adj=c(0.1,-0.5), col=“red”, cex=0.8) text(maxattb$t, maxattb$maxatt, expression(underline(rho)[min]), adj=c(0.1,1.5), col=“red”, cex=0.8) text(31, upinertiab, expression(bar(rho)[infinity]), adj=c(0.1,-0.5), col=“red”, cex=0.8) text(31, lowinertiab, expression(underline(rho)[infinity]), adj=c(0.1,1.5), col=“red”, cex=0.8)

Amplification bounds result from the projection of a population with 100% stage x individuals. Attenuation bounds result from the projection of a population with 100% stage 1 individuals.

FIGURE 3: TRANSFER FUNCTIONS

Fig. 3a: Transfer function of asymptotic growth

This figure is designed to be 3.5” by 3.5” (Check size of plot window using ‘par(din)’).

Set margins: par(mar=c(5,4,1,1))

Create a transfer function using ‘tfa’. The perturbation structure is determined by two vectors d and e. The matrix d%*%t(e) gives the structure, where nonzero elements in this matrix are the elements of the PPM to be perturbed. The relative size of entries in this matrix are the relative sizes of perturbation to those elements. In this case, we are perturbing element [5,4]. We are going to look at the effect of perturbing up to 0.25. The largest biologically reasonable perturbation is about 0.12. tf1 <- tfa(TF, d=c(1,0,0,0), e=c(0,0,1,0), prange=seq(0,0.25,0.01))

Now we plot this using an S3 method for transfer functions (for information see ‘?plot.tfa’). plot(tf1, cex.axis=0.8)

Now we’re going to add in the sensitivity tangent. This has an intercept of lambda-max, and a slope of the sensitivity of the same transfer function. Calculate lambda-max of the desert tortoise PPM: lambda <- Re(eigen(LaeliaZ1)$values[1])

Calculate the sensitivity using the function ‘tfsens’: sens1 <- tfsens(TF, d=c(0,0,0,1), e=c(0,0,1,0))

Now add in the line, specifying the correct intercept and slope: abline(lambda, sens1, lty=2, col=“red”)

Fig. 3b: Transfer function of population inertia

This figure is designed to be 3.5” by 3.5” (Check size of plot window using ‘par(din)’).

Set margins: par(mar=c(5,4,1,1))

The process is very similar to above. We need to specify a PPM, perturbation structure and perturbation range. For inertia we either have to specify a population vector using the ‘vector’ argument, or the bound to be calculated using the ‘bound’ argument. Create a population vector: n0 <- c(1,8,13,21)

tf1 <- tfa(TF, d=c(0,0,0,1), e=c(0,0,1,0), prange=seq(0,0.25,0.01))

Now calculate the transfer function using inertia.tfa: tf2 <- inertia.tfa(TF, vector=n0, d=c(0,0,0,1), e=c(0,0,1,0), prange= seq(0,0.25,0.01))

Plot the transfer function using the same S3 method as before: plot(tf2, cex.axis=0.8, ylim=c(3.9,4.43))

The sensitivity tangent for transfer function of inertia has an intercept of equal to the relevant inertia (either using the same population vector, or the correct bound), and a slope of the sensitivity of the same transfer function. Calculate inertia of the desert tortoise PPM using the population vector: inertia <- inertia(TF, vector=n0)

Calculate the sensitivity using the function ‘inertia.tfsens’: sens2 <- inertia.tfsens(TF, vector=n0, d=c(0,0,0,1), e=c(0,0,1,0), tolerance=1e-5)

(Here the ‘tolerance’ has had to be lowered to avoid calculation error: try the function without that argument and it will have trouble running)

Now add in the line, specifying the correct intercept and slope: abline(inertia, sens2, lty=2, col=“red”)

FIGURE 4: TRANSFER FUNCTION MATRIX

This figure is designed to be 7” by 7” (Check size of plot window using ‘par(din)’).

This is a nice, easy plot because the function does it all for you. The functions ‘tfmat’ and ‘inertia.tfmat’ calculate a transfer function for every PPM element. They are saved as arrays of values. The functions are customisable: see ‘?tfmat’ and ‘?inertia.tfmat’.

Create the array for inertia, using a specific population vector: n0 <- c(48, 16, 12, 10) tfmat <- inertia.tfamatrix(TF, vector=n0)

…and plot it! plot(tfmat)

n0 <- c(48, 16, 12, 10) tfmat <- tfamatrix(TF)

…and plot it! plot(tfmat)

Lepanthes rubripetala

BIOL4558

Agosto 2021

APPENDIX S1

Load the library

Articulo para guiar su aprendizaje

Lepanthes rubripetala population #3

How to construct a matrix in R

Crecimiento poblacional intrinsico

Ejercicio 1

Ejercicio 2

Dos posible problemas se tiene que considerar antes de hacer los analisis

Ergodica

Irreducible

Realidad de la recopilación de datos

Now project the population for x years in the future.

Primitive Matrix

Distribución estable de la población, w

Elasticidad

Elasticities

Stable Stage distribution.

Damping Ratio

Convergence Time

TRANSIENT DYNAMICS