Tarea_1_Historia_de_Vida
BIOL4558
Agosto 2021
library(tidyverse)
library(gt)
#library(kableExtra)Ejercicios
En este Ejercicio, Ud. podrá en practica los métodos de análisis aprendido en el capitulo 3, las paginas 50-71. Los datos provienen de dos especies de herbáceas de Noruega, Dactylorhiza lapponica y Gymnadenia conopsea. Los datos fueron recolectado de parcelas permanentes del 1982 al 2000. El articulo se encuentra en este enlace here.
P1 Con los datos de la tabla 4 en el articulo. Produzca una gráfica similar a la figura 1.6 en el libro de Gotelli. Añadir ambas secuencias (ambas especies) en la misma gráfica. Asegurar que los ejes esten bien identificados (Subir la grafica a Edmodo)
Number_Ind= tribble(
~Species, ~Year, ~N,
"Dl", 1982, 36,
"Dl", 1983, 18,
"Dl",1984, 71,
"Dl", 1985, 23,
"Dl",1986, 29,
"Dl",1987, 21,
"Dl",1988, 5,
"Dl", 1989, 72,
"Dl", 1990, 74,
"Dl", 1991, 39,
"Dl", 1992, 72,
"Dl", 1993, 35,
"Dl",1994, 43,
"Dl", 1995, 34,
"Dl",1996, 45,
"Dl", 1997, 42,
"Dl", 1998, 78,
"Dl", 1999, 30,
"Dl", 2000, 35,
"Gc", 1982, 2,
"Gc", 1983, 5,
"Gc",1984, 19,
"Gc", 1985, 16,
"Gc",1986, 10,
"Gc",1987, 9,
"Gc",1988, 10,
"Gc", 1989, 16,
"Gc", 1990, 22,
"Gc", 1991, 25,
"Gc", 1992, 25,
"Gc", 1993, 7,
"Gc",1994, 31,
"Gc", 1995, 18,
"Gc",1996, 25,
"Gc", 1997, 71,
"Gc", 1998, 51,
"Gc", 1999, 27,
"Gc", 2000, 24,
)Number_Ind## # A tibble: 38 × 3
## Species Year N
## <chr> <dbl> <dbl>
## 1 Dl 1982 36
## 2 Dl 1983 18
## 3 Dl 1984 71
## 4 Dl 1985 23
## 5 Dl 1986 29
## 6 Dl 1987 21
## 7 Dl 1988 5
## 8 Dl 1989 72
## 9 Dl 1990 74
## 10 Dl 1991 39
## # ℹ 28 more rowsNumber_Ind %>%
ggplot(aes(Year, N, color=Species)) +
geom_point()+
geom_line() +
scale_x_continuous(breaks = seq(1982, 2000, by = 1))+
theme(axis.text.x = element_text(angle = 75, vjust = 0.5, hjust=.5))+
ylab("Cantidad de individuos \n en flor en cada año")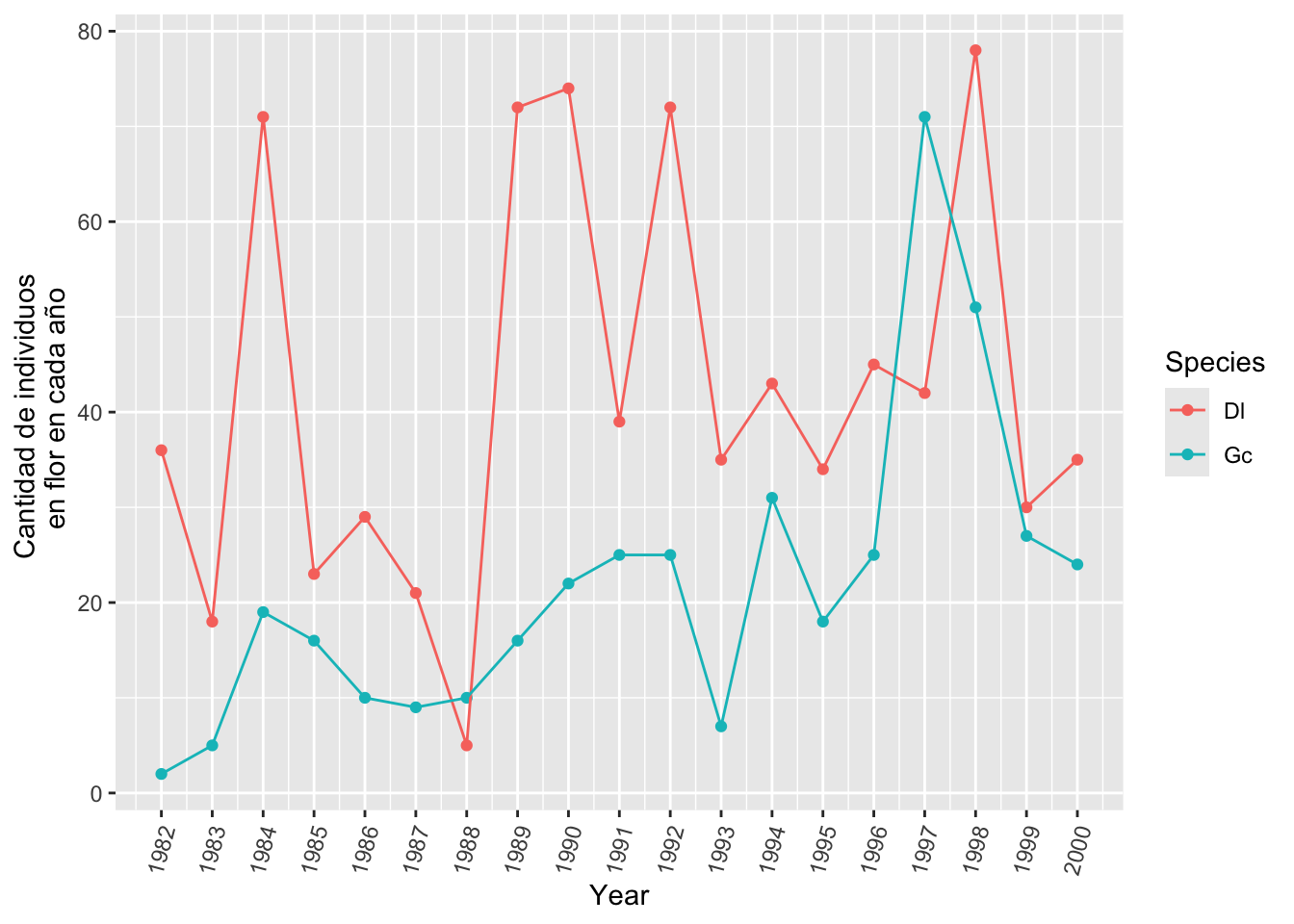
P2 Usando el resultado de la gráfica anterior
(contestar en EDMODO) - Determina si el crecimiento poblacional es
exponencial.
- Explica su interpretación. - De por lo menos dos razones ecológicas
que limitaría el crecimiento exponencial
P3 Con los datos abajo que estan representado en la
tabla 6 del articulo, incluyo aqui informacióin ficticia sobre la
fecundidad.
- Haga los siguientes cálculos ANTES contestar las preguntas. Presenta
una tabla similar Gotelli (Table 3.1) con los datos.
- Calcula gx
- Calcula Ro
Razón de mortandad
- Calcula qx, explica como se calcula este indice
Largo de una generación
- Calcula G
Asegurate de contestar TODAS la preguntas.
Contestar en Edmodo
- Cual es la edad que la supervivencia es más alta (para ambas situación, synthed and unscythed)
- Cual es la edad que la supervivencia es más baja (para ambas situación, synthed and unscythed)
- Basado en esta formula anterior, cual es la edad que hay mayor probabilidad de morir y cual es el la razón para plantes en el ambiente unsynthed?
- Cual es la edad donde hay menor probabilidad de morir?
- Cual es el largo de una “Generación” (para ambas situación, synthed and unscythed)
- Cual es el estimado de r (para ambas situación, synthed and unscythed).
- Que efecto tiene el manejo del sitio (unscythed and scythed) sobre la supervivencia de los individuos de este especies.
Aquí están los datos. NOTA que en el articulo no hay datos de fecundidad por consecuencia se añadió aquí unos datos ficticios. Los datos don para Dactylorhiza lapponica (Unscythed), y D. lapponica (Scythed)
Life_Table = tribble(
~Species, ~Treatment, ~Year_after_first_flowering, ~N, ~lx, ~bx,
"Dl", "Unscythes", 0, 142, 1.00, 1,
"Dl", "Unscythes", 1, 111, 0.78,1,
"Dl", "Unscythes",2, 94, 0.66,1,
"Dl", "Unscythes",3, 86, 0.61,1,
"Dl", "Unscythes",4, 77, 0.54,1,
"Dl", "Unscythes",5, 72, 0.51,1,
"Dl", "Unscythes",6, 70, 0.49,1,
"Dl", "Unscythes",7, 63, 0.44,.9,
"Dl", "Unscythes",8, 59, 0.42,.7,
"Dl", "Unscythes",9, 58,0.41,.5,
"Dl", "Unscythes",10, 49,0.35,.1,
)
gt(Life_Table)| Species | Treatment | Year_after_first_flowering | N | lx | bx |
|---|---|---|---|---|---|
| Dl | Unscythes | 0 | 142 | 1.00 | 1.0 |
| Dl | Unscythes | 1 | 111 | 0.78 | 1.0 |
| Dl | Unscythes | 2 | 94 | 0.66 | 1.0 |
| Dl | Unscythes | 3 | 86 | 0.61 | 1.0 |
| Dl | Unscythes | 4 | 77 | 0.54 | 1.0 |
| Dl | Unscythes | 5 | 72 | 0.51 | 1.0 |
| Dl | Unscythes | 6 | 70 | 0.49 | 1.0 |
| Dl | Unscythes | 7 | 63 | 0.44 | 0.9 |
| Dl | Unscythes | 8 | 59 | 0.42 | 0.7 |
| Dl | Unscythes | 9 | 58 | 0.41 | 0.5 |
| Dl | Unscythes | 10 | 49 | 0.35 | 0.1 |