if (!require("pacman")) install.packages("pacman")
pacman::p_load(QuantPsyc, car, tidyverse, sjPlot)


library(QuantPsyc)
library(car)
library(ggplot2)
library(tidyverse)
library(sjPlot)

Regresión Polinomial

Si la gráfica de residuos de la regresión lineal indica una distribución no aleatoria del error de predicción del modelo lineal es posible que pueda mejorar su predicción utilizando una regresión con un término cuadrático (es decir, \(X^2\)), por lo que ahora tenemos una regresión con un polinomio.

Construcción de un modelo con polinomio. Usamos los datos de 15 observaciones de mujeres en el archivo women en el paquete datasets. Los datos representan la altura (en pulgadas) y el peso (en libras) de 15 mujeres entre las edades de 30 a 39.

Nota aquí que se usa I(x^2) para añadir el monomio \(x^2\) . Ahora nuestro modelo evaluará el efecto de la regresión lineal y cuadrática. El resumen del modelo se observa que el modelo incluye tanto el intercepto, la ecuación lineal y el término cuadrático, y cada uno es significativo. Esto quiere decir que tanto el modelo lineal como el polinomio explican parte de la varianza. NOTA como se indica que un valor

fit2 <- lm(weight ~ height + I(height^2), data=women)
summary(fit2)
## 
## Call:
## lm(formula = weight ~ height + I(height^2), data = women)
## 
## Residuals:
##      Min       1Q   Median       3Q      Max 
## -0.50941 -0.29611 -0.00941  0.28615  0.59706 
## 
## Coefficients:
##              Estimate Std. Error t value Pr(>|t|)    
## (Intercept) 261.87818   25.19677  10.393 2.36e-07 ***
## height       -7.34832    0.77769  -9.449 6.58e-07 ***
## I(height^2)   0.08306    0.00598  13.891 9.32e-09 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.3841 on 12 degrees of freedom
## Multiple R-squared:  0.9995, Adjusted R-squared:  0.9994 
## F-statistic: 1.139e+04 on 2 and 12 DF,  p-value: < 2.2e-16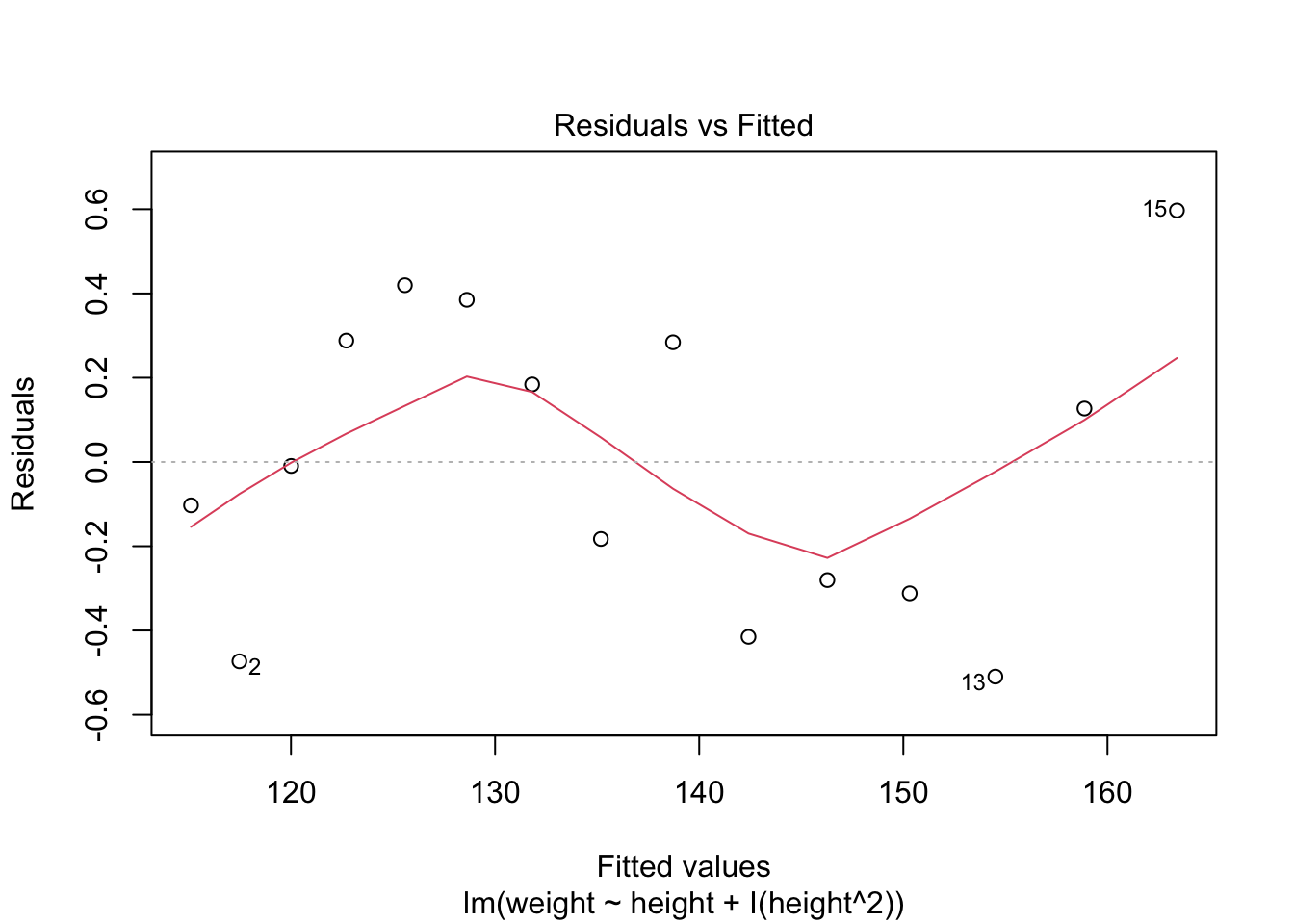
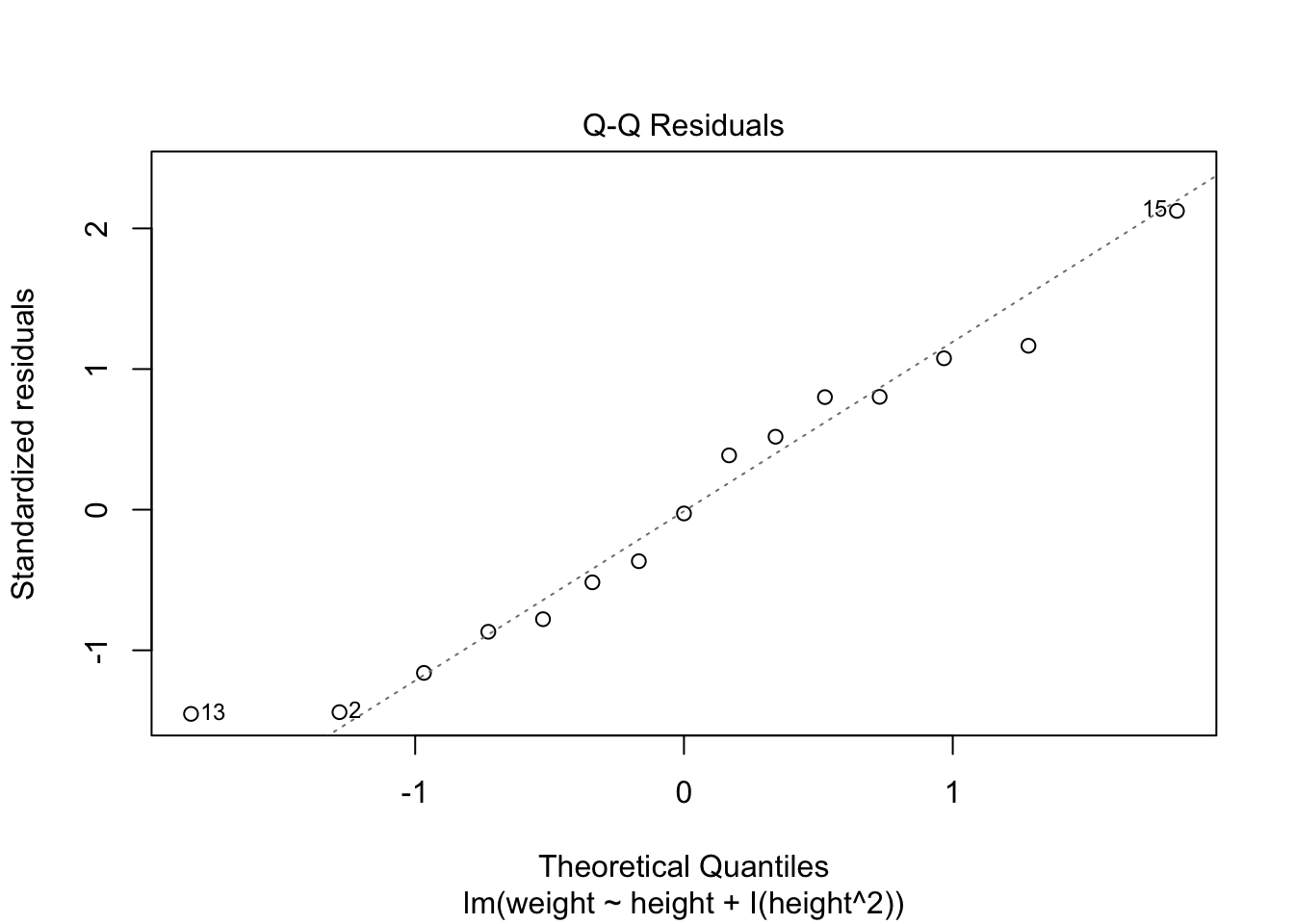
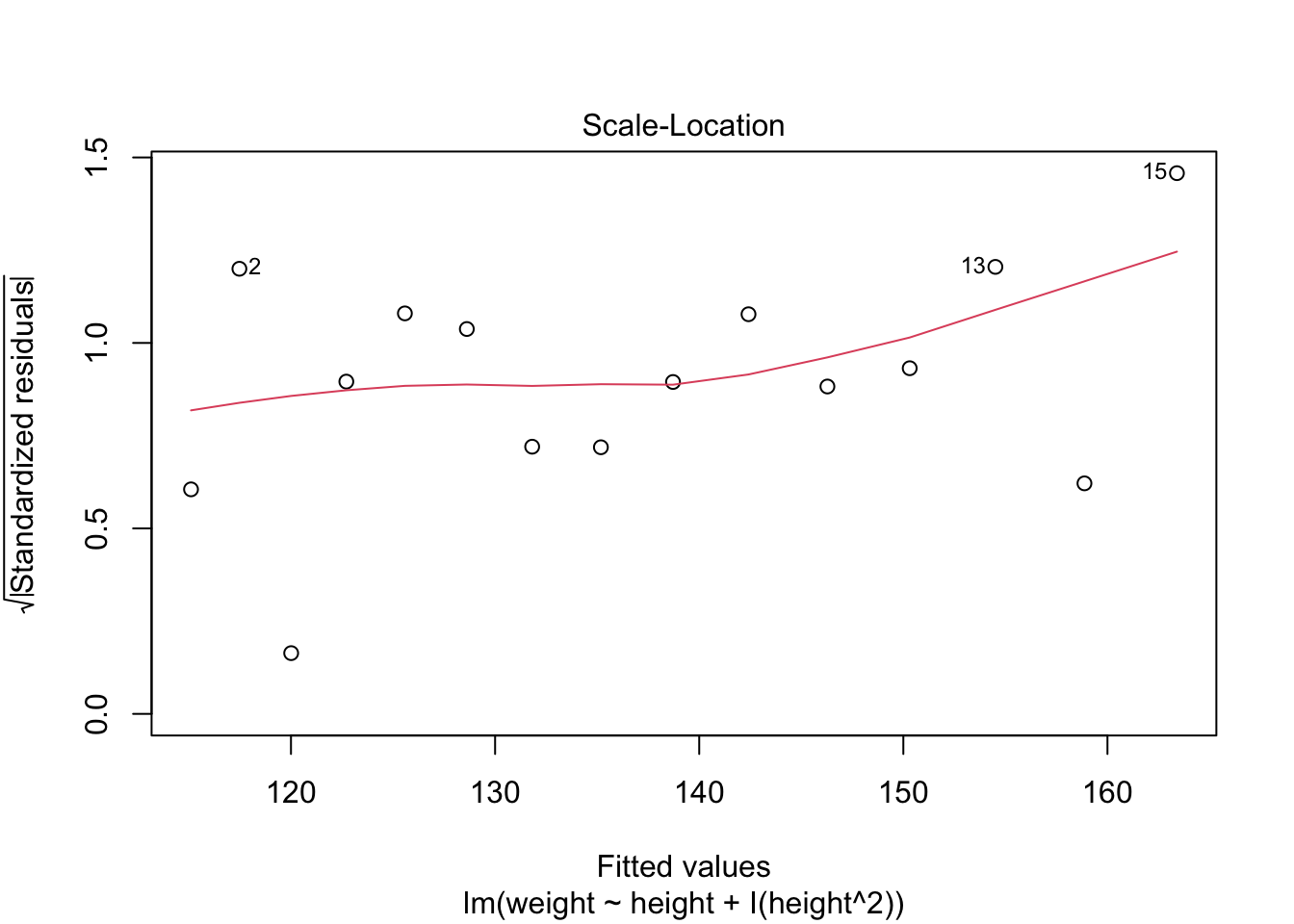
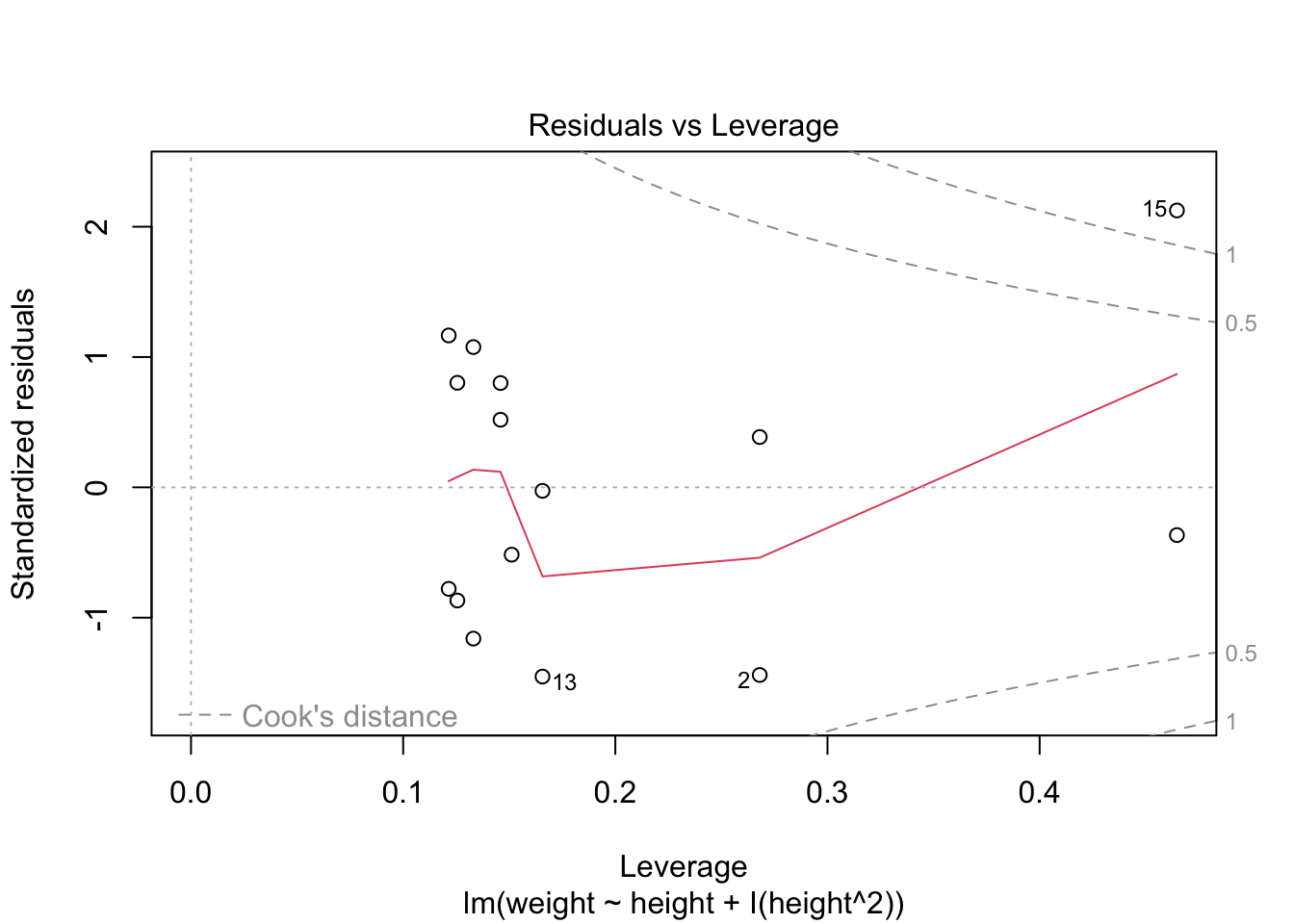
plot(fit2)

Comparar el modelo anterior con el siguiente modelo. En el presente modelo se removio el polinimio. Evaluando los residuales es claro que estos no son distribuido de forma al azar. Note la curva. Esto es un indicador que no cumple con el supuesto de igualdad de varianza.

fit2 <- lm(weight ~ height, data=women)
summary(fit2)
## 
## Call:
## lm(formula = weight ~ height, data = women)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -1.7333 -1.1333 -0.3833  0.7417  3.1167 
## 
## Coefficients:
##              Estimate Std. Error t value Pr(>|t|)    
## (Intercept) -87.51667    5.93694  -14.74 1.71e-09 ***
## height        3.45000    0.09114   37.85 1.09e-14 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 1.525 on 13 degrees of freedom
## Multiple R-squared:  0.991,  Adjusted R-squared:  0.9903 
## F-statistic:  1433 on 1 and 13 DF,  p-value: 1.091e-14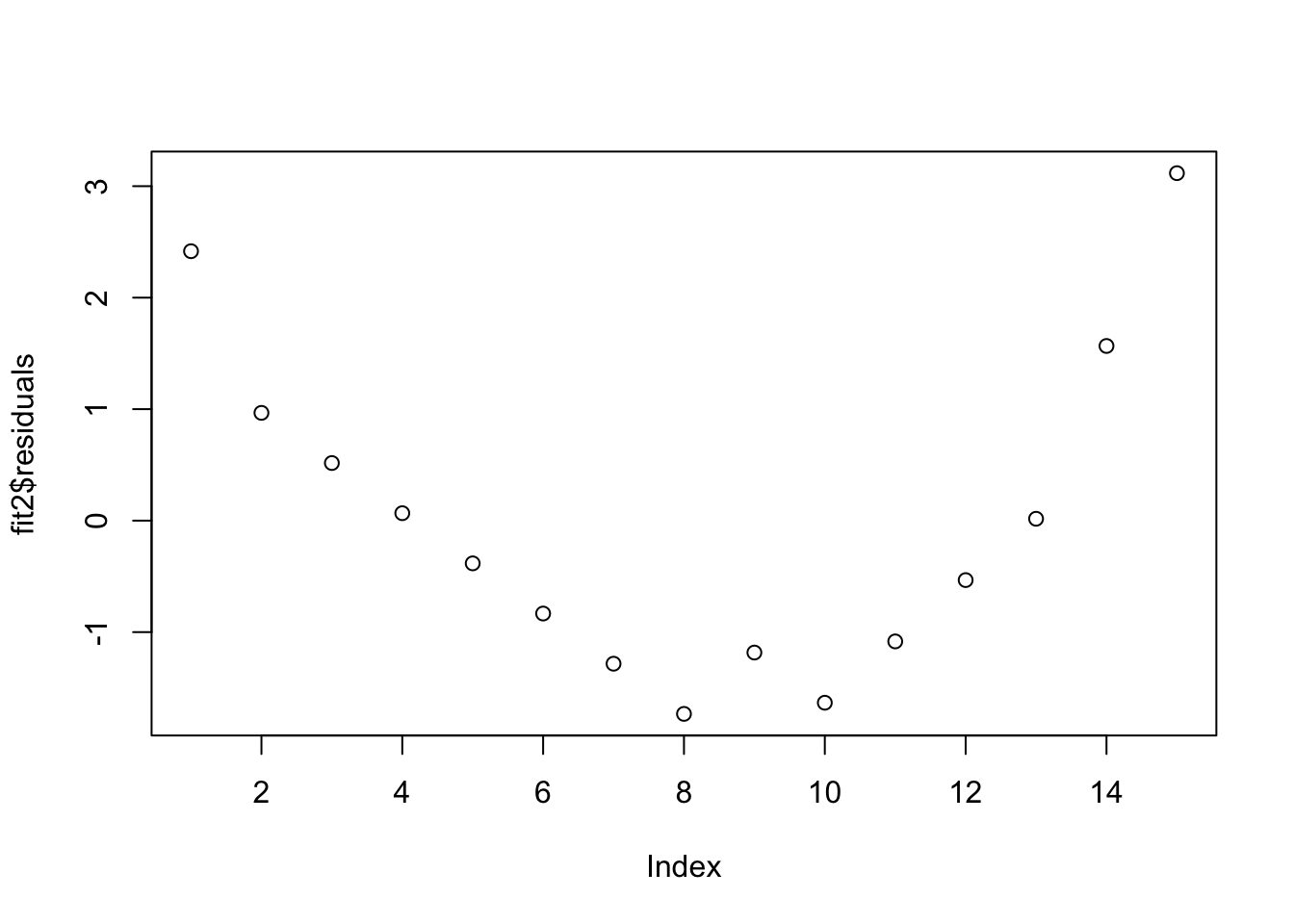
plot(fit2$residuals)

Visualizando el gráfico.

Nota que la linea azul representa el modelo de regresión lineal y la linea roja representa el modelo \(y \approx ax^2 +bx+c\). Es claro que el modelo \(y \approx ax^2+bx+c\) es un mejor modelo ya que los datos se acercan más a la linea.

ggplot(women, aes(height, weight)) +
  geom_point(color ="blue", size=2) +
  geom_smooth(method=lm)+
  stat_smooth(aes(), method = "lm", formula = y ~ poly(x,2), 
              color ="red", se =TRUE, size = 1) +
  labs(x="Height, inches", y="Weight, lb.")
## `geom_smooth()` using formula = 'y ~ x'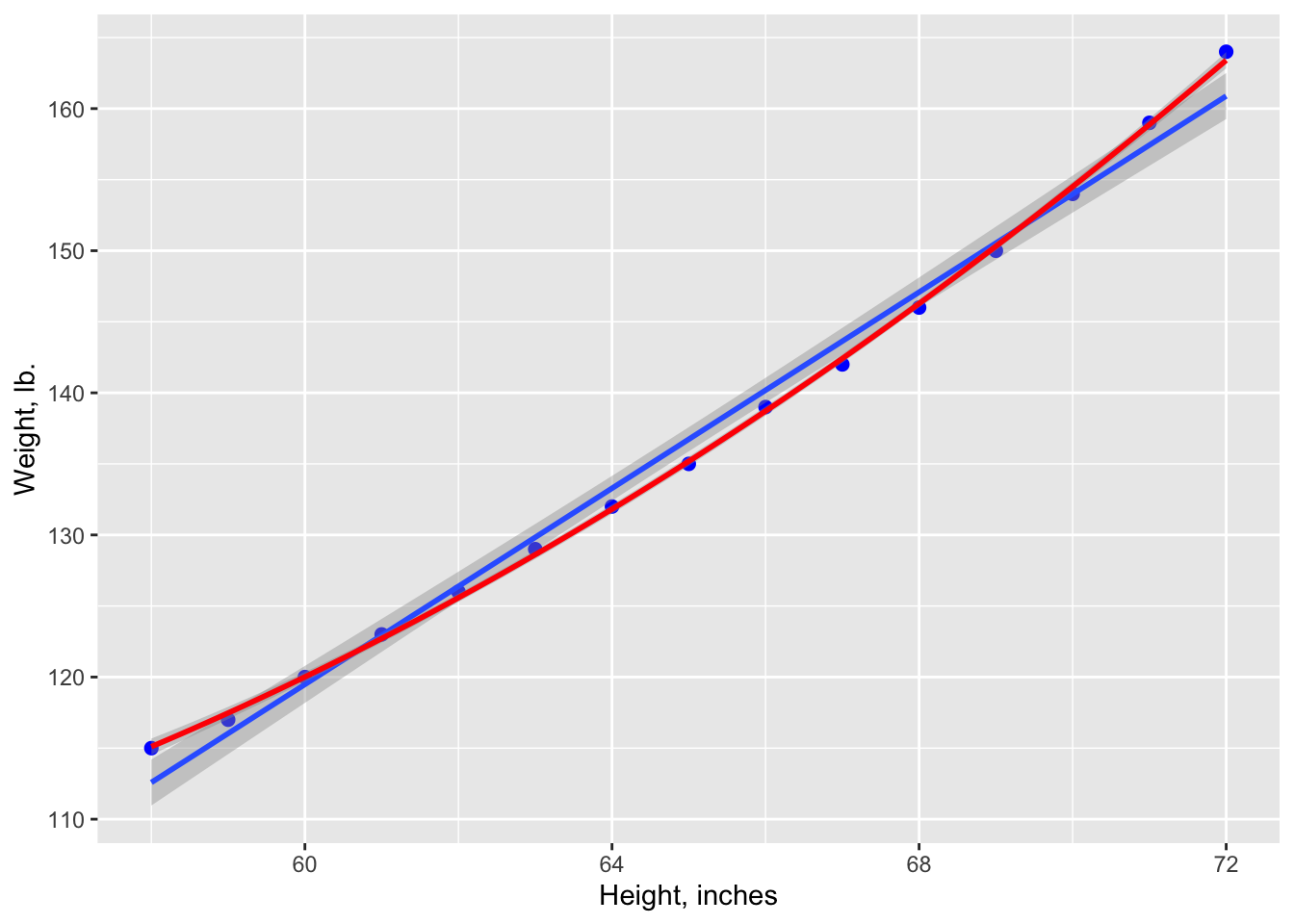

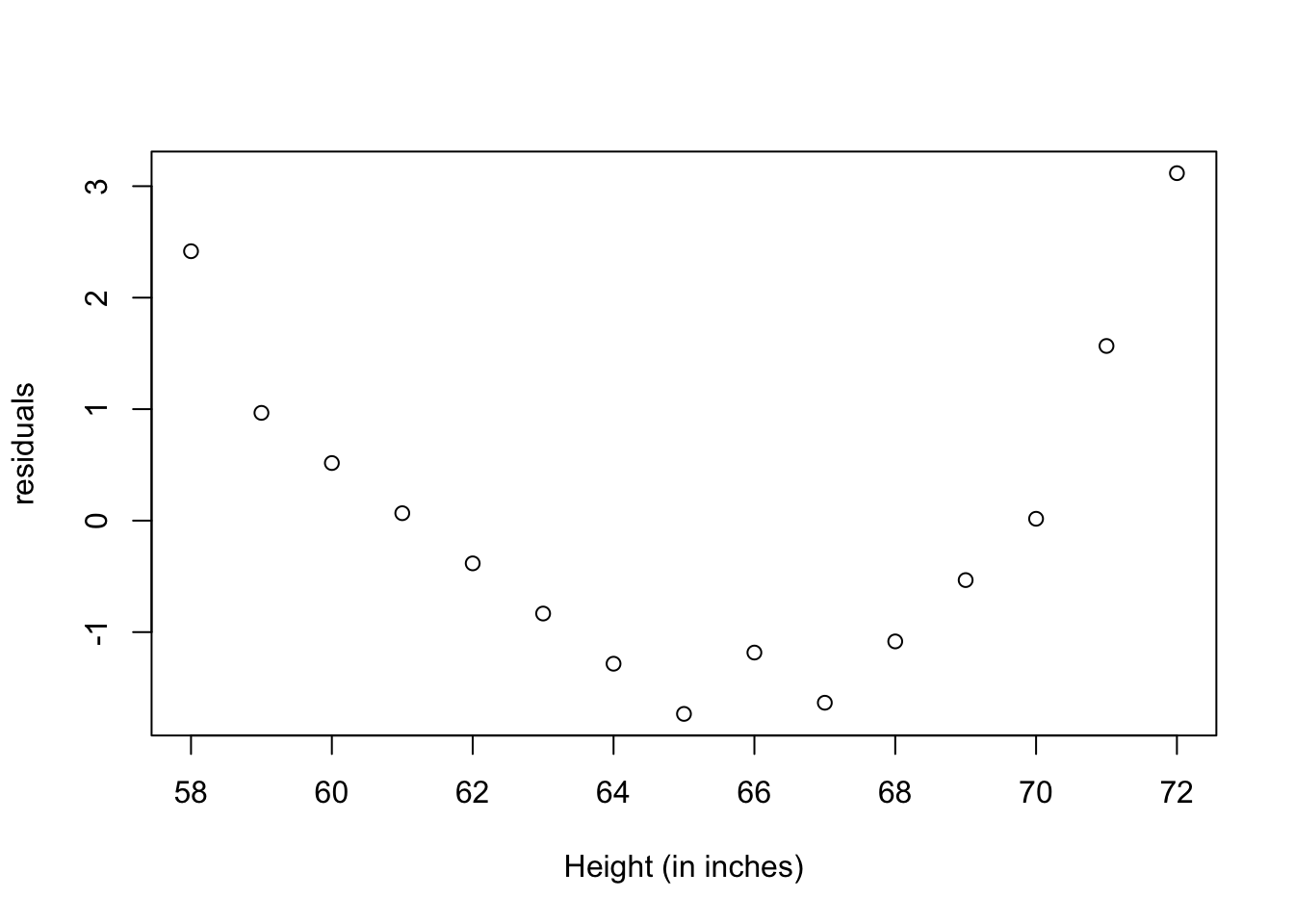
Visualizando los residuales

Recuerda que los residuales tienen que ser normalmente distribuidos a través de la variables de x. En este caso vemos que los residuales no están concentrados en un área de la gráfica. Por ejemplo los residuales no son más grande en los valores de x más grande.

plot(women$height,residuals(fit2),
     xlab="Height (in inches)",
     ylab="residuals")

La nueva ecuación polinomial es la siguiente:

\[y=\alpha+b_1x_i+b_2x_i^2+\epsilon\]

donde el intercepto \(\alpha\) más los dos coeficientes, \(b_1\) para el componente lineal y el componente cuadrático \(b_2\), el \(\epsilon\) son los errores.

\[y=261.9-7.35*x_i+0.08*x_i^2\]

tab_model(
  fit2,show.df = TRUE,show.stat = TRUE,
  CSS = list(
    css.depvarhead = 'color: red;',
    css.centeralign = 'text-align: left;', 
    css.firsttablecol = 'font-weight: bold;', 
    css.summary = 'color: blue;'
  )
)
  weight
Predictors Estimates CI Statistic p df
(Intercept) -87.52 -100.34 – -74.69 -14.74 <0.001 13.00
height 3.45 3.25 – 3.65 37.86 <0.001 13.00
Observations 15
R2 / R2 adjusted 0.991 / 0.990

Interpretación de la tabla de resultados

La cantidad de variación contabilizada ha aumentado al 99,9%. La significación del término cuadrático (t = 13.89, p <0.001) sugiere que la inclusión del término cuadrático mejora el ajuste del modelo. El error de predicción (residuales) es menor y su distribución parece más aleatoria.

Modelo cúbico

Aquí un ejemplo para evaluar si los datos tienen una distribución cúbica. Primero creamos un conjunto de datos.

Los valores en la variable x

d<-seq(from=0, to=20, by=0.1)

Los valores a predecirse en la variable y

y<-500+0.5*(d-10)^3

Crear un conjunto de datos que tiene variación. Donde los datos tienen una variación con distribución normal con un promedio de 10 y una desviación estándar de 80.

variación <- rnorm(length(d), mean=10, sd=80)
var.y <- y + variación

Unir los datos un un tibble

df=tibble(y,var.y, d)

Visualizar los datos con el polinomio cúbico.

ggplot(df, aes(d, var.y)) +
  geom_point(color ="blue", size=2) +
  stat_smooth(method = "lm", formula = y ~ poly(x,3), 
              color ="red", se =TRUE, size = 1)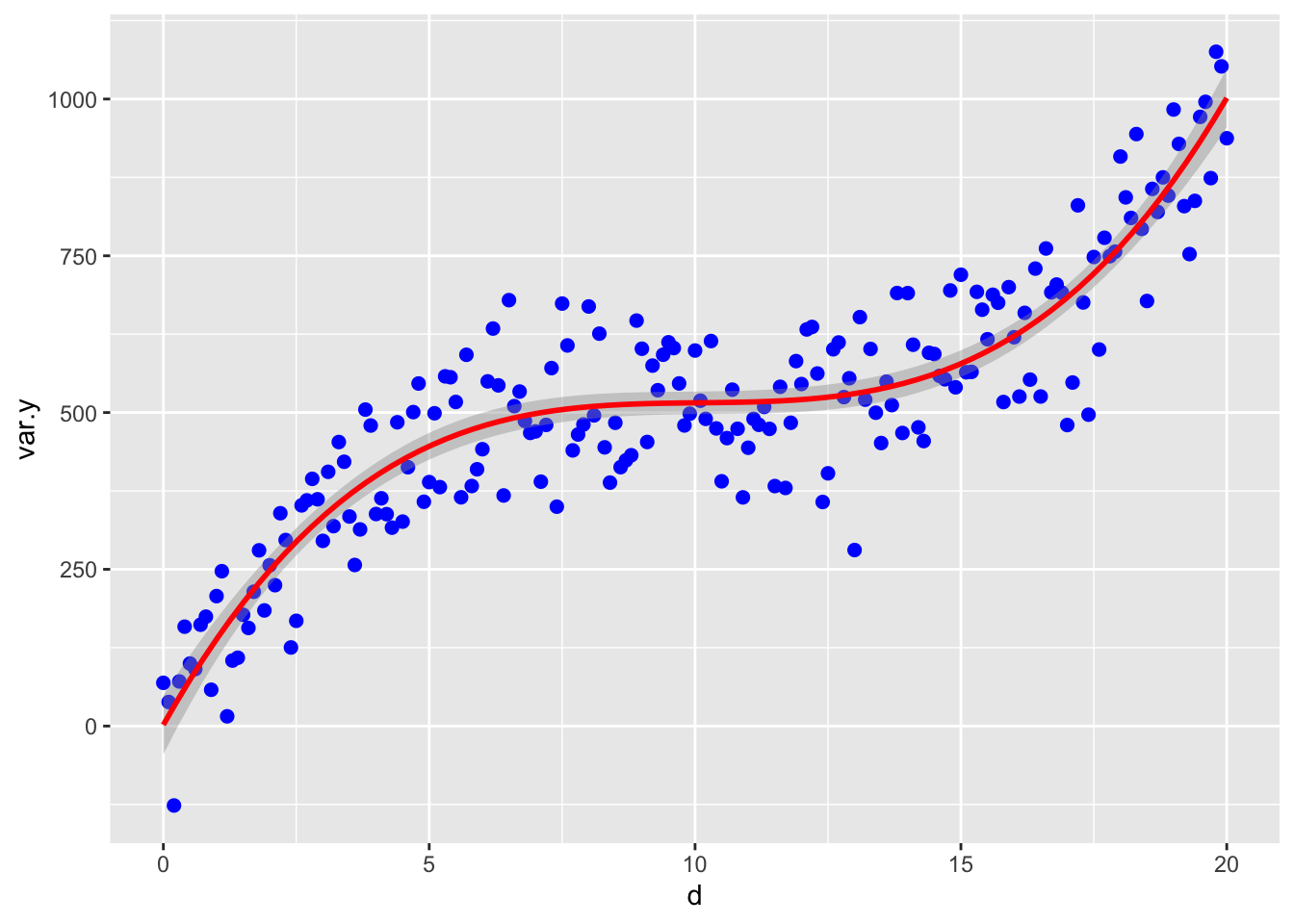

Ahora vemos como se ve los modelos de regresión lineal y cuadratico. nota que los datos siguen mucho mejor la curva cúbica.

ggplot(df, aes(d, var.y)) +
  geom_point(color ="blue", size=2) +
  geom_smooth(method=lm, color="blue")+
  stat_smooth(method = "lm", formula = y ~ poly(x,2), 
              color ="orange", se =TRUE, size = 1)+
  stat_smooth(method = "lm", formula = y ~ poly(x,3), 
              color ="red", se =TRUE, size = 1)
## `geom_smooth()` using formula = 'y ~ x'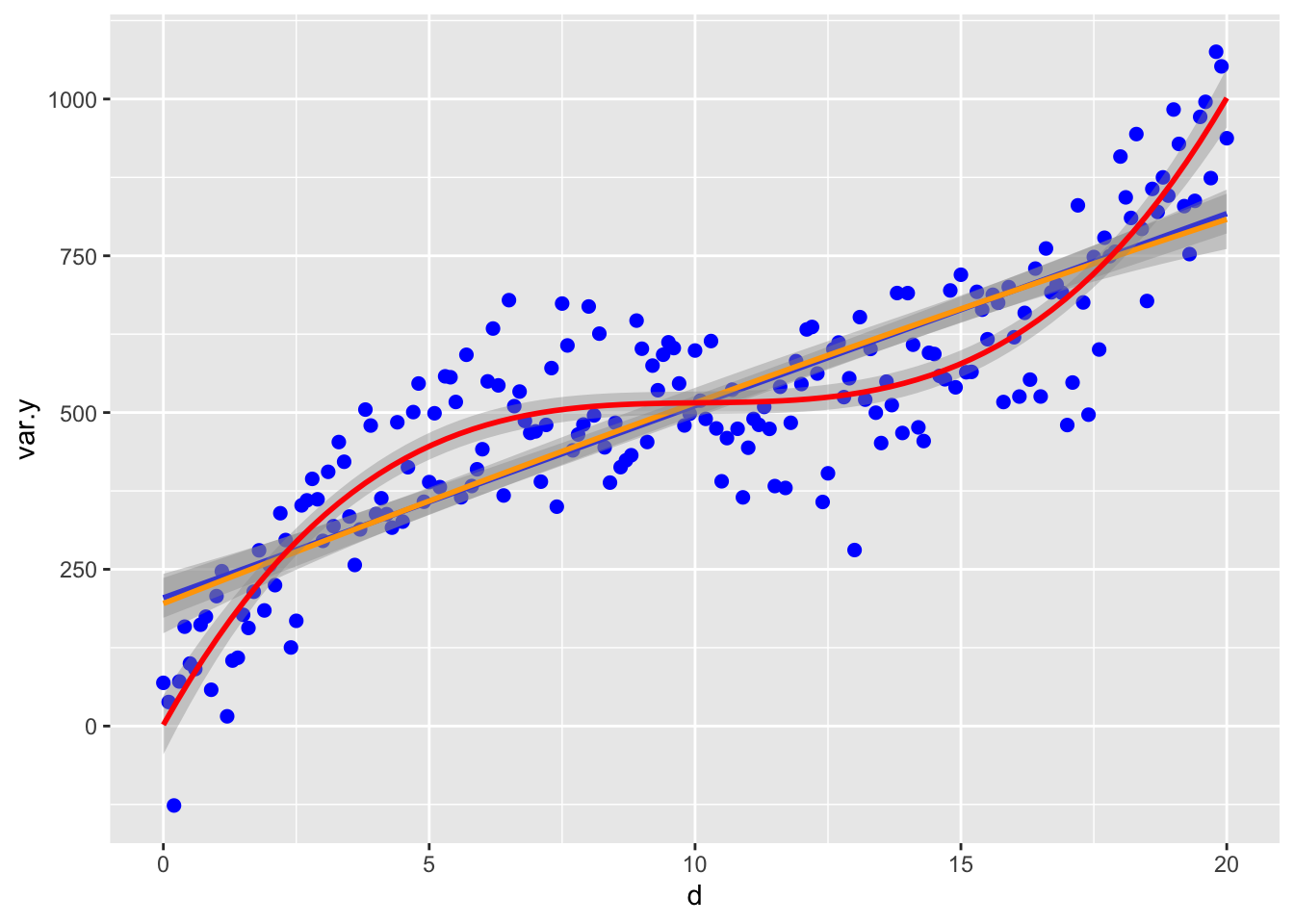

Construir el modelo cubico

fit3 <- lm(var.y ~ d + I(d^2)+ I(d^3), data=df)


tab_model(
  fit3,show.df = TRUE,show.stat = TRUE,
  CSS = list(
    css.depvarhead = 'color: red;',
    css.centeralign = 'text-align: left;', 
    css.firsttablecol = 'font-weight: bold;', 
    css.summary = 'color: blue;'
  )
)
  var y
Predictors Estimates CI Statistic p df
(Intercept) 1.97 -45.13 – 49.07 0.08 0.934 197.00
d 150.90 130.46 – 171.35 14.56 <0.001 197.00
d^2 -14.86 -17.24 – -12.49 -12.32 <0.001 197.00
d^3 0.49 0.41 – 0.57 12.38 <0.001 197.00
Observations 201
R2 / R2 adjusted 0.837 / 0.834

Los residuales del modelo

Se observa que los residuales están distribuido uniformemente entre todos los valores de la variable en x. Por consecuencia se cumple con el supuesto de Igualdad de varianza.

plot(df$d,residuals(fit3))

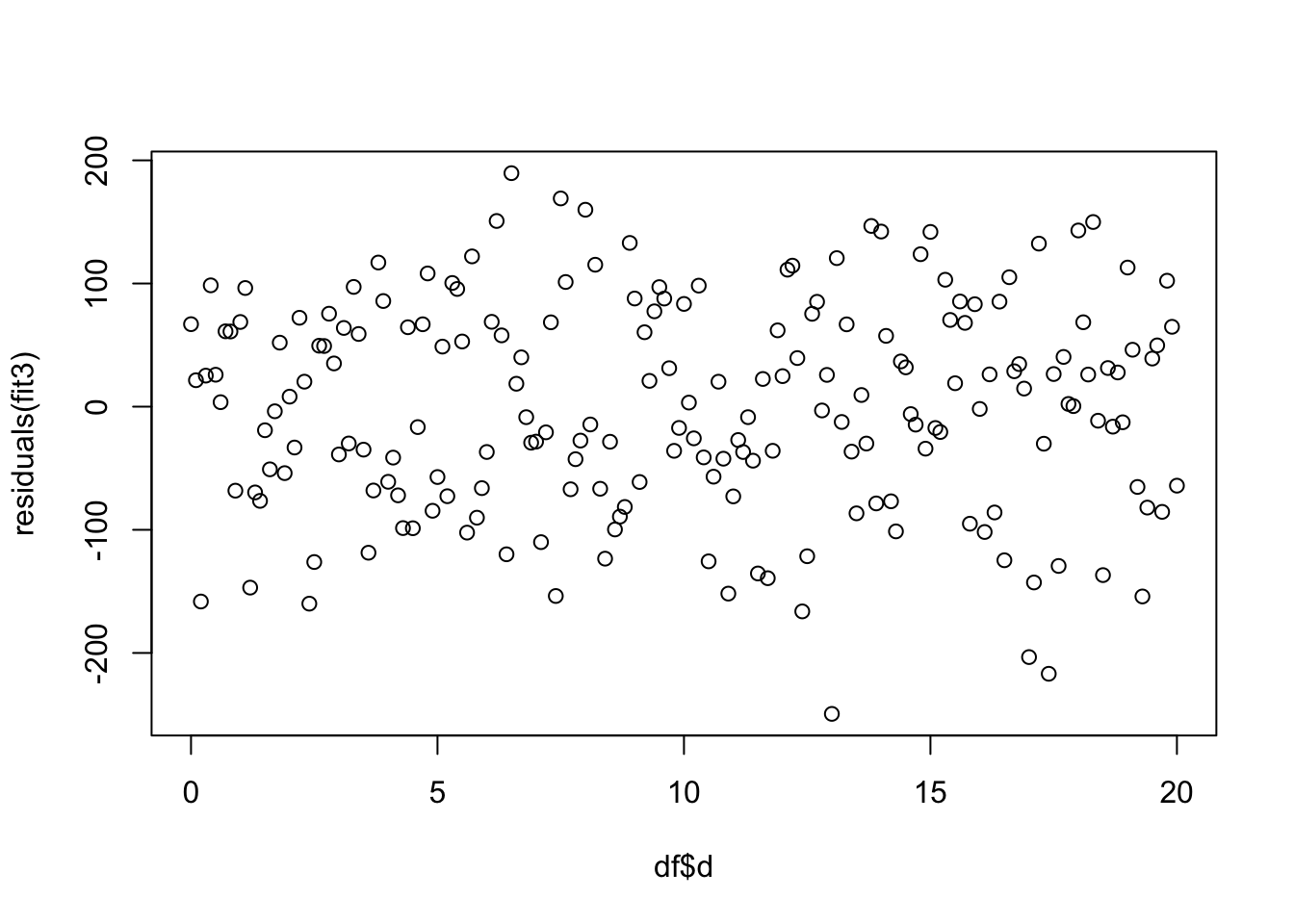
Interpretación de la tabla de resultados

La cantidad de variación contabilizada toma en cuenta 84.6% de la variación total. La significación del término cuadrático (t = 13.31, p <0.001) sugiere que la inclusión del término cubica mejora el ajuste del modelo. El error de predicción (residuales) es menor y su distribución parece más aleatoria.

Residuales y patrones

Evidencia de Residuales que no cumple con Igualdad de varianza.

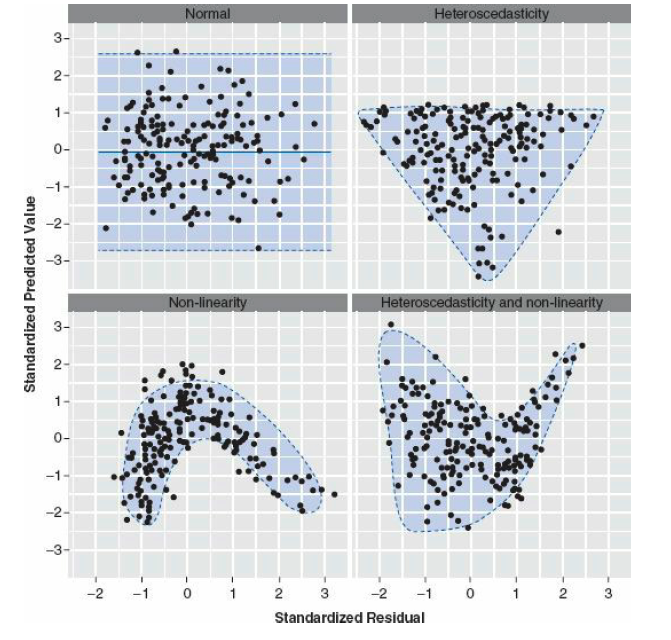
Aquí se demuestra algunos de los patrones que pueden sugerir que los datos no cumplen con los supuestos de la prueba. El gráfico es de Field, Miles and Field del libro Discovering Statistics Using R, 2012. La figure 7.15 (Con permiso del autor A. Field, email, 2020-10-08) .

  • En el gráfico arriba a la izquierda es una distribución de los datos que sugiere igualdad de varianza o homogeneidad de varianza.

  • En el gráfico arriba a la derecha demuestra un patrón de residuales donde los residuales no son distribuido equitativamente, y sugiere heteroscadastiticidad de varianza.

  • En el gráfico abajo a la izquierda un patrón donde sugiere que la relación entre una variable y otra no es lineal.

  • En el gráfico abajo a la derecha se observa un patrón de residuales donde tanto los datos son heteroescadisticidad y no-lineal.

knitr::include_graphics("Graficos/Residuals_heteroscadasticity.png")

“Activities reported in this website was supported by the National Institute of General Medical Sciences of the National Institutes of Health under Award Number R25GM121270. The content is solely the responsibility of the authors and does not necessarily represent the official views of the National Institutes of Health.”