library(ggplot2)
library(arm)
library(coefplot)
library(tidyverse)

Regresión Poisson

La regresión Poisson es parte de los modelos lineales generalizados (GLM) y se utiliza cuando la variable de respuesta son conteos, unidades discretas no negativas.

Los datos provienen del libro y ejemplos de Jared Lander, R for Everyone, 2nd Edition, Addison Wesley Data & Analitics Series, 2017.

acs=read.table("https://jaredlander.com/data/acs_ny.csv", sep=",", header=TRUE, stringsAsFactors = FALSE)



library(readr)
#acs_ny <- read_csv("acs_ny.csv")
#acs=acs_ny
head(acs)
AcresFamilyIncomeFamilyTypeNumBedroomsNumChildrenNumPeopleNumRoomsNumUnitsNumVehiclesNumWorkersOwnRentYearBuiltHouseCostsElectricBillFoodStampHeatingFuelInsuranceLanguage
1-10150Married4139Single detached10Mortgage1950-1959180090NoGas2500English
1-10180Female Head3246Single detached20RentedBefore 193985090NoOil0English
1-10280Female Head4028Single detached31Mortgage2000-20042600260NoOil6600Other European
1-10330Female Head2124Single detached10Rented1950-19591800140NoOil0English
1-10330Male Head3125Single attached10MortgageBefore 1939860150NoGas660Spanish
1-10480Male Head0341Single detached00RentedBefore 1939700140NoGas0English

Qué es una distribución Poisson

La distribución de Poisson se usa cuando tenemos valores numéricos discretos, \(0, 1, 2, 3, 4, \ldots, k, \ldots\) pero no puede tener valores parciales como \(1.4\)

La formulación de la regresión de Poisson es \({ y }_{ i }~ pois({ \theta }_{ i })\) donde \({ y }_{ i }\) es la i-ésima respuesta y \[{ \theta }_{ i }={ e }^{ { X }_{ i }\beta}\] es la media de la distribución para la i-ésima observación.

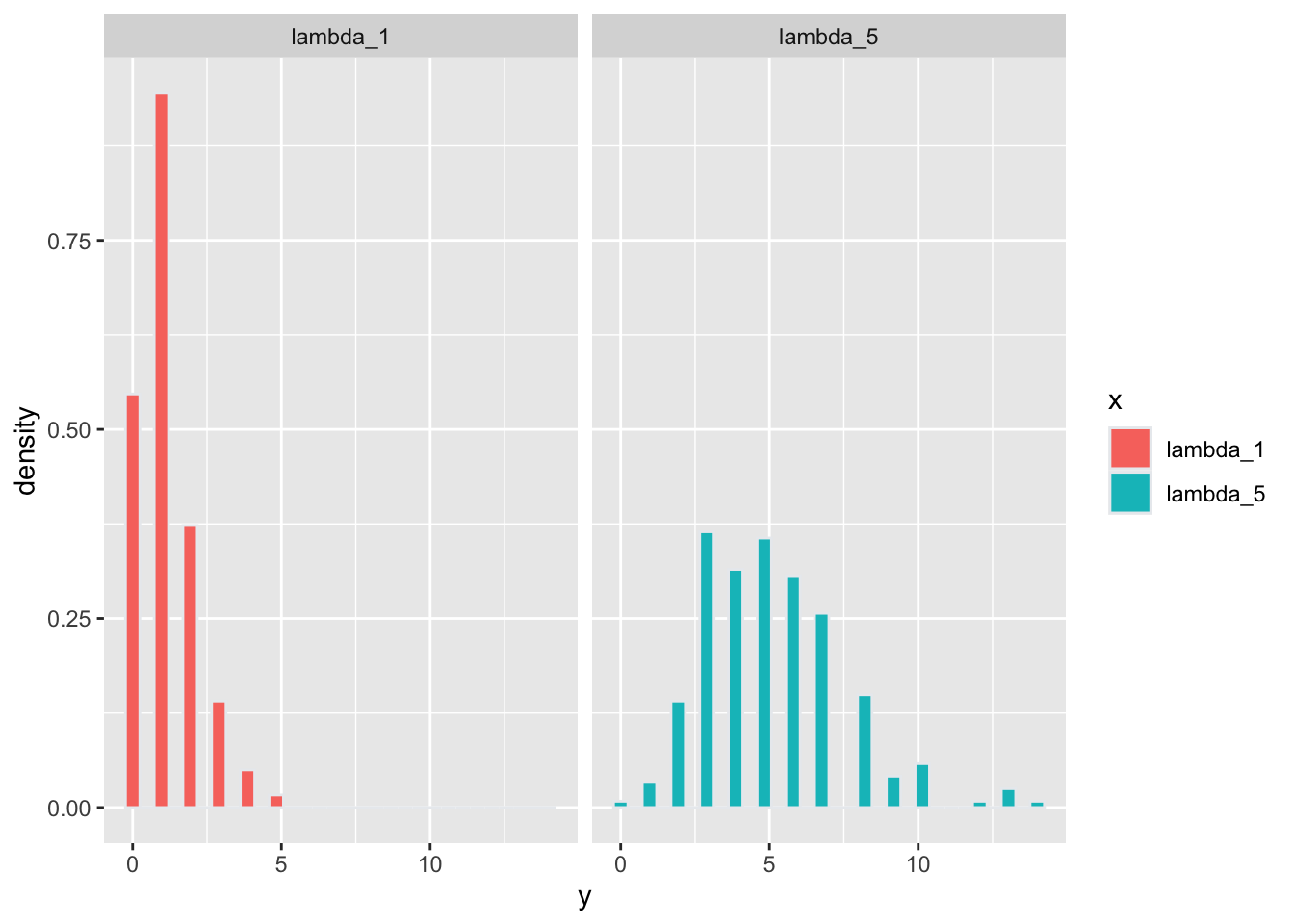
Para el primer ejercicio nota aquí que los datos son la cantidad de hijos por familia. El primer punto que hay que apreciar es que los valores son unidades, y que estos no puede haber 1.1, medio hijo o -1 hijo. En otras palabras es que los datos son discretos y no negativos. Entonces la distribución Poisson es una variable x de datos al azar y discreta y tiene una distribución Poisson si los parámetros \(\lambda\) > 0, para k = 0,1,2,….k, y la función de probabilidad es igual a

\[Pr\left(x=k\right)=\frac{\lambda^k\cdot e^{-\lambda}}{k!}\]

donde

  • e es igual al valor de Euler, e=2.71828…
  • k es el número de ocurrencias.
  • k! es el factorial de k.

Cuando se describe una distribución Poisson el promedio es \(\lambda\) y la varianza es también \(\lambda\). Es el mismo valor. Para la descripción de los otras medidas de tendencia centrales y de dispersión vea el website de Wikipedia (https://en.wikipedia.org/wiki/Poisson_distribution).

Información básica

Notación: Pois( \(\lambda\) )

Parametros: \(\lambda\in (0, inf)\) (Números naturales comenzando en zero)

Promedio: \(\lambda\)

Varianza: \(\lambda\)

Mediana: \(\approx [\lambda +1/3 -0.02/\lambda]\)

Skewness: \(\lambda^{-1/2}\)

Kurtosis: \(\lambda^{-1}\)

Distribución de frecuencia de distribución Poisson

Las figuras de la frecuencia demuestran el comportamiento de la distribución de Poisson cuando \(\lambda\) aumenta. Se han generado 500 valores al azar en cada simulación donde \(\lambda\) es 1, 5, 15 y 25. Nota que si \(\lambda = 1\) entonces el promedio es uno y la varianza es 1. A medida \(\lambda \rightarrow \infty\) (y la muestra es grande la distribución se acerca a una distribución normal.

ggplot(lambda, aes(y, fill=x))+
geom_histogram(color="#e9ecef")+
  facet_wrap(~x, scales="free_y")+
  ylab("Frecuencia")+
  xlab("k")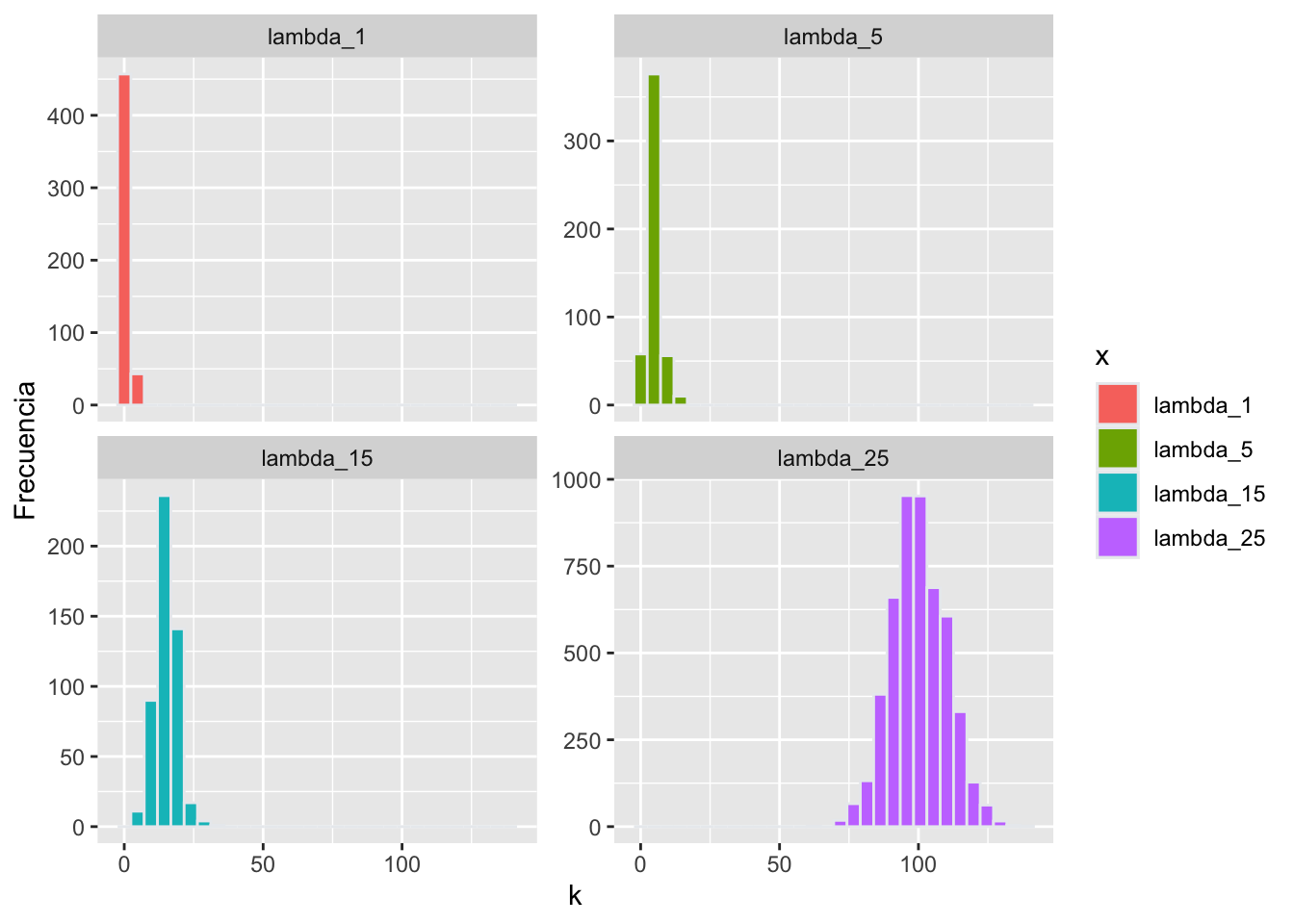

Función de Probabilidad

Se puede convertir estos gráficos en una “probability mass distribution”. En esta ocasión la distribución sigue la siguiente ecuación,

\[Pr\left(x=k\right)=\frac{\lambda^k\cdot e^{-\lambda}}{k!}\]

La suma de \(Pr\left(x=k\right)\) es igual a uno.

ggplot(lambda, aes(y, fill=x))+
geom_histogram(aes(y=..density..), color="#e9ecef")+
  facet_wrap(~x)+
  ylab("P(X=k)")+
  xlab("k")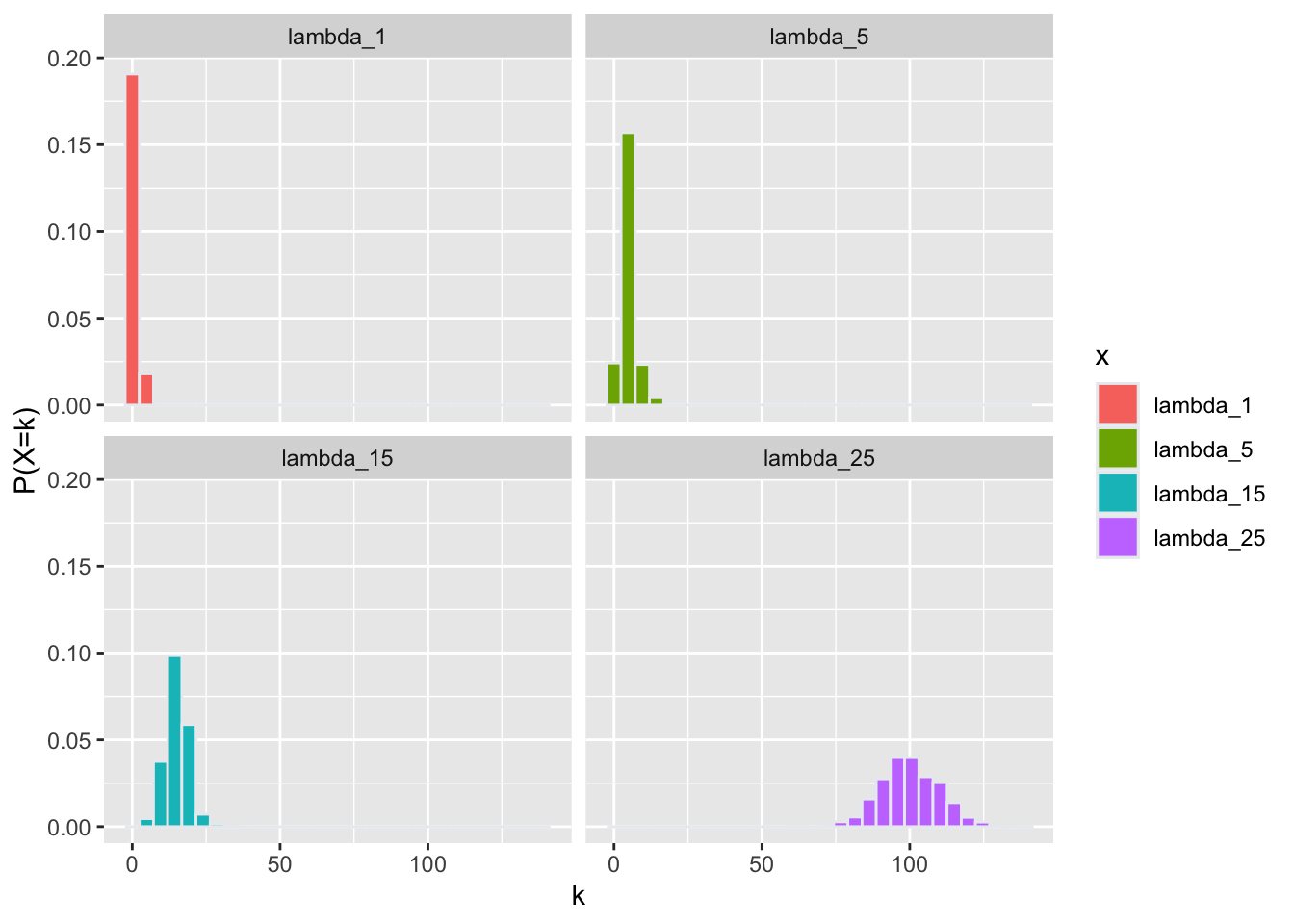

Acercamiento a las dos primeras graficas.

  • Nota que la cantidad/proporción de cada grupo es discreta.

  • Segundo no sigue una distribución norma.

#lambda
lambda %>%  filter(x==c("lambda_1", "lambda_5")) %>% 
  ggplot(aes(y, fill=x))+
geom_histogram(aes(y=..density..), color="#e9ecef")+
facet_wrap(~x)

Probabilidades cumulativas

Aquí se aplica la función para visualizar la probabilidades acumulativas, vea stat_ecdf {ggplot2} para más detalles. Lo que se observa es la probabilidad de incluir los valores acumulativos (i.e. \(f(k) = P(X \leq k)\) . Lo más importante es reconocer que la adición de las probabilidades no es continua, pero “salta” de un valor a otra a medida que se añade la frecuencia de los valores en el eje de x. Si fuese una distribución normal, la linea seria suavizada. Nota que cuando el valor de \(\lambda\) es más grande los saltos son más pequeños (es más suave el cambio).

ggplot(lambda, aes(y, colour=x))+
stat_ecdf(geom = "step")+
  ylab("P(X=k)")+
  xlab("k")

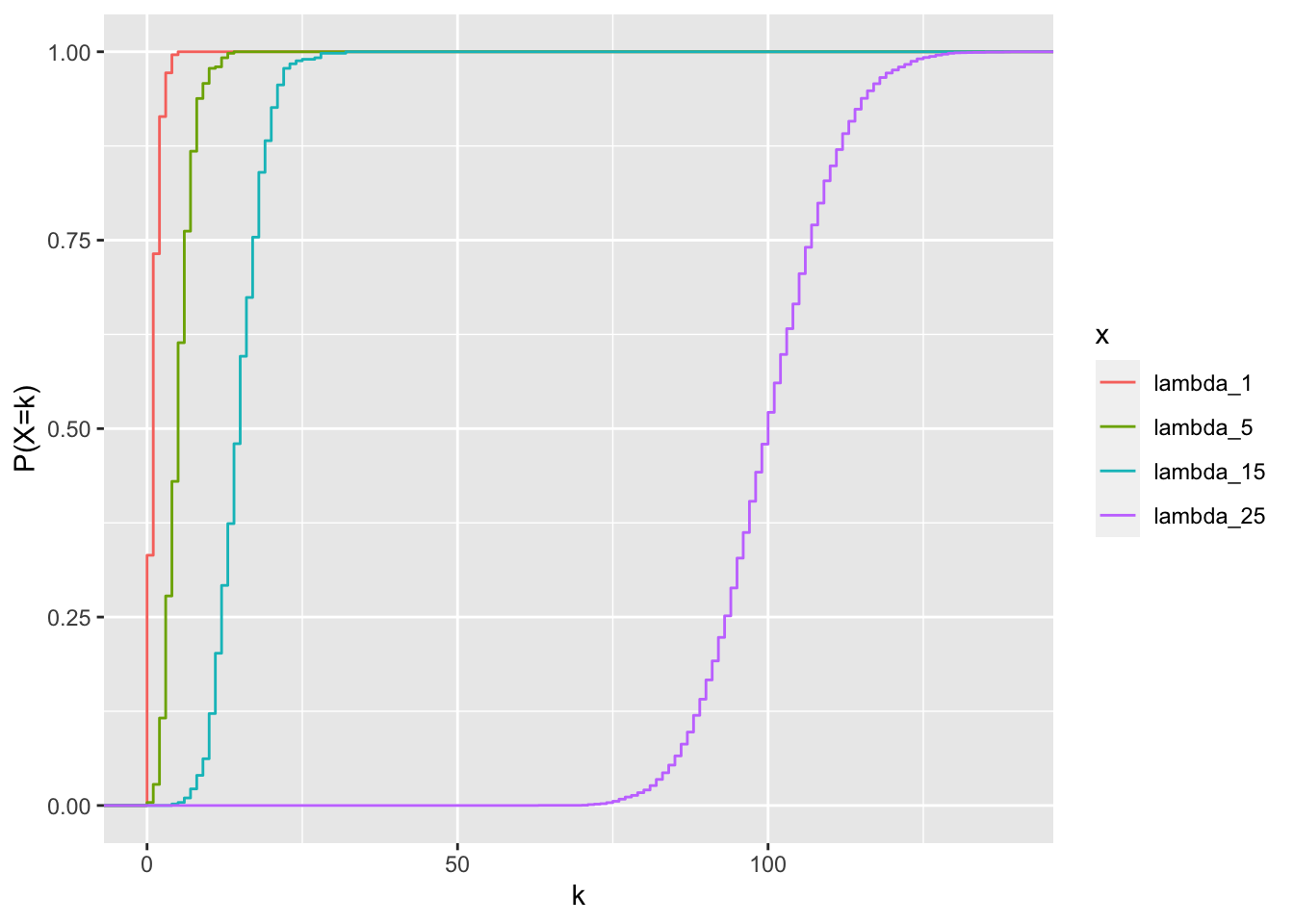
Ejemplo de tamaño de muestra grande con un lambda grande (lo importante es que no este cerce de zero)

ggplot(lambda2, aes(y, fill=x))+
geom_histogram(aes(y=..density..), color="#e9ecef")+
  ylab("P(X=k)")+
  xlab("k")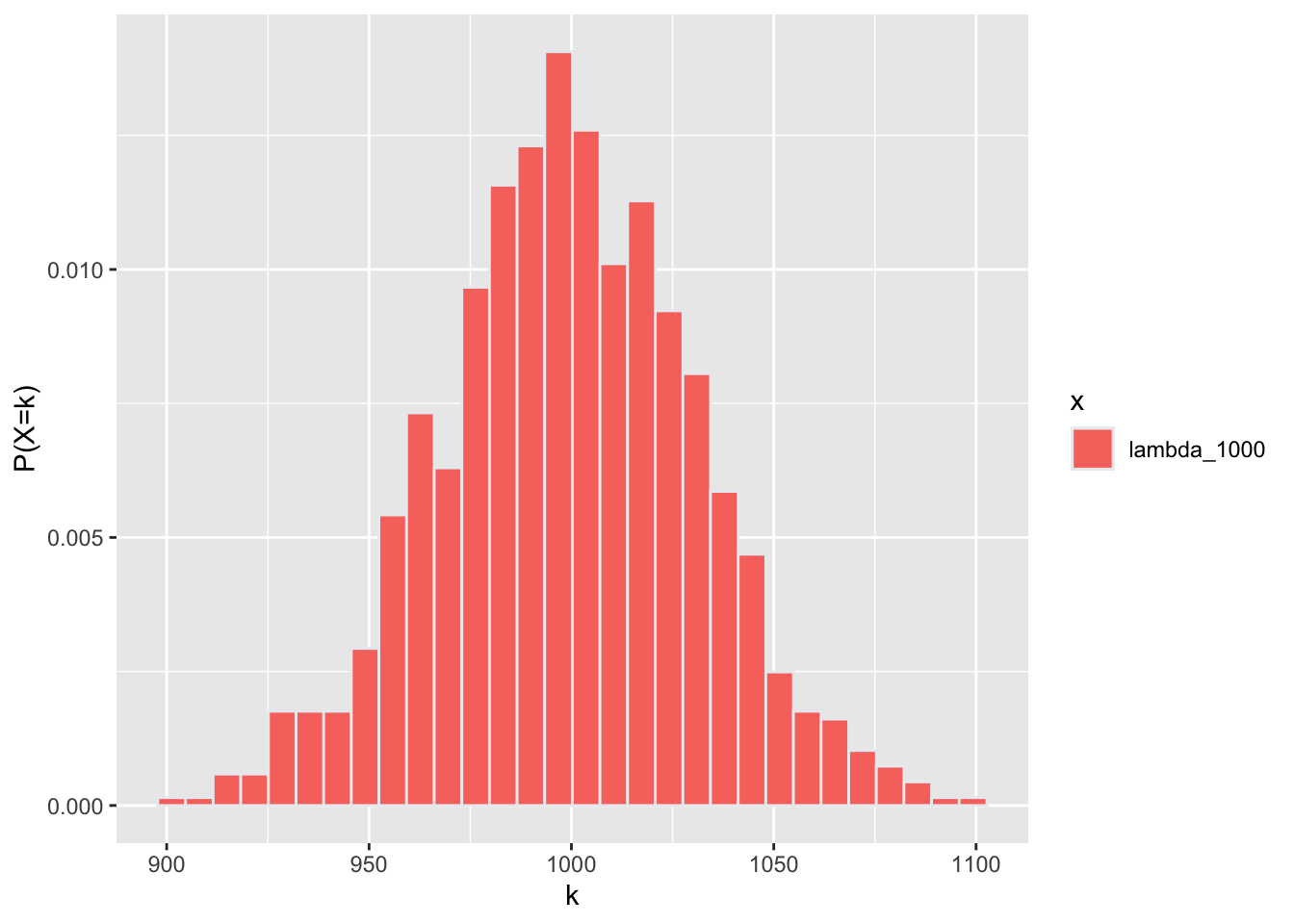

Ejemplos de Datos Poisson

Muchas veces los datos recolectados tienen la característica de ser discretos y no negativos. Ejemplos:

  • El número de hijos por mujer.
  • El número de errores ortográficos en una frase de 100 palabras
  • El número de animales muertos en la carretera por una distancia especifica
  • El número de mutaciones en una cadena de ADN
  • El número de estudiantes por salón
  • El número de frutos por planta

Regresión Poisson

El primer paso es evaluar la variable dependiente. Miramos las variables del archivo.

head(acs)
AcresFamilyIncomeFamilyTypeNumBedroomsNumChildrenNumPeopleNumRoomsNumUnitsNumVehiclesNumWorkersOwnRentYearBuiltHouseCostsElectricBillFoodStampHeatingFuelInsuranceLanguage
1-10150Married4139Single detached10Mortgage1950-1959180090NoGas2500English
1-10180Female Head3246Single detached20RentedBefore 193985090NoOil0English
1-10280Female Head4028Single detached31Mortgage2000-20042600260NoOil6600Other European
1-10330Female Head2124Single detached10Rented1950-19591800140NoOil0English
1-10330Male Head3125Single attached10MortgageBefore 1939860150NoGas660Spanish
1-10480Male Head0341Single detached00RentedBefore 1939700140NoGas0English

La variable dependiente en nuestro análisis es el número de hijos NumChildren. Se observa que la mayoría de las familias no tienen hijos,

ggplot(acs, aes(x=NumChildren))+ 
  geom_histogram(bindwidth=1, fill="#376889")+
  scale_x_continuous(breaks = round(seq(min(acs$NumChildren), max(acs$NumChildren), by = 1),1))
## Warning in geom_histogram(bindwidth = 1, fill = "#376889"): Ignoring unknown
## parameters: `bindwidth`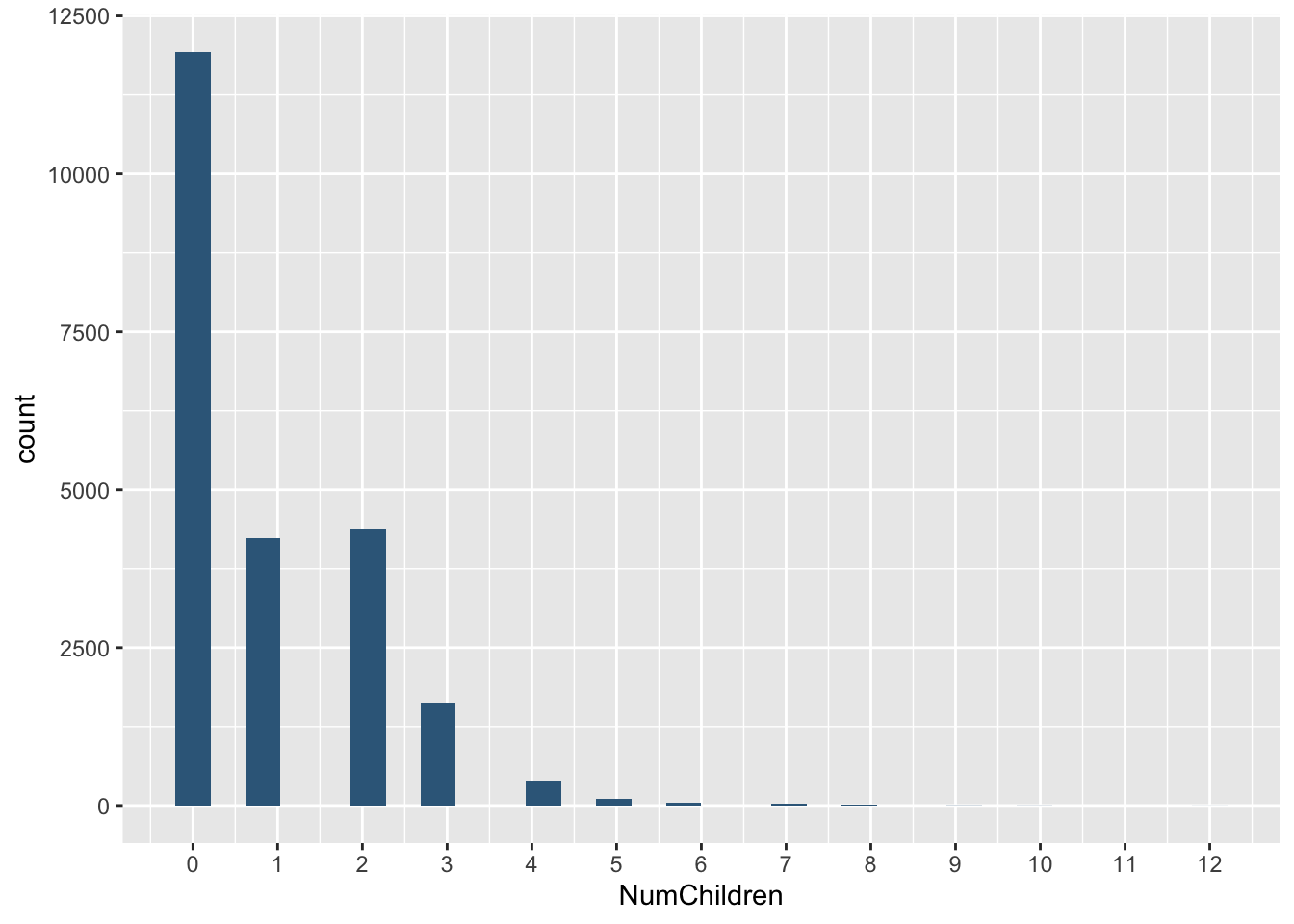

Modelo Poisson

El modelo de regresión Poisson usa la función glm() y una transformación log con la siguiente función family=poisson(link=“log”).

children1<-glm(NumChildren~FamilyIncome+FamilyType+OwnRent,
               data=acs, family=poisson(link="log"))

summary(children1)
## 
## Call:
## glm(formula = NumChildren ~ FamilyIncome + FamilyType + OwnRent, 
##     family = poisson(link = "log"), data = acs)
## 
## Coefficients:
##                       Estimate Std. Error z value Pr(>|z|)    
## (Intercept)         -3.257e-01  2.103e-02 -15.491  < 2e-16 ***
## FamilyIncome         5.420e-07  6.572e-08   8.247  < 2e-16 ***
## FamilyTypeMale Head -6.298e-02  3.847e-02  -1.637    0.102    
## FamilyTypeMarried    1.440e-01  2.147e-02   6.707 1.98e-11 ***
## OwnRentOutright     -1.974e+00  2.292e-01  -8.611  < 2e-16 ***
## OwnRentRented        4.086e-01  2.067e-02  19.773  < 2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## (Dispersion parameter for poisson family taken to be 1)
## 
##     Null deviance: 35240  on 22744  degrees of freedom
## Residual deviance: 34643  on 22739  degrees of freedom
## AIC: 61370
## 
## Number of Fisher Scoring iterations: 5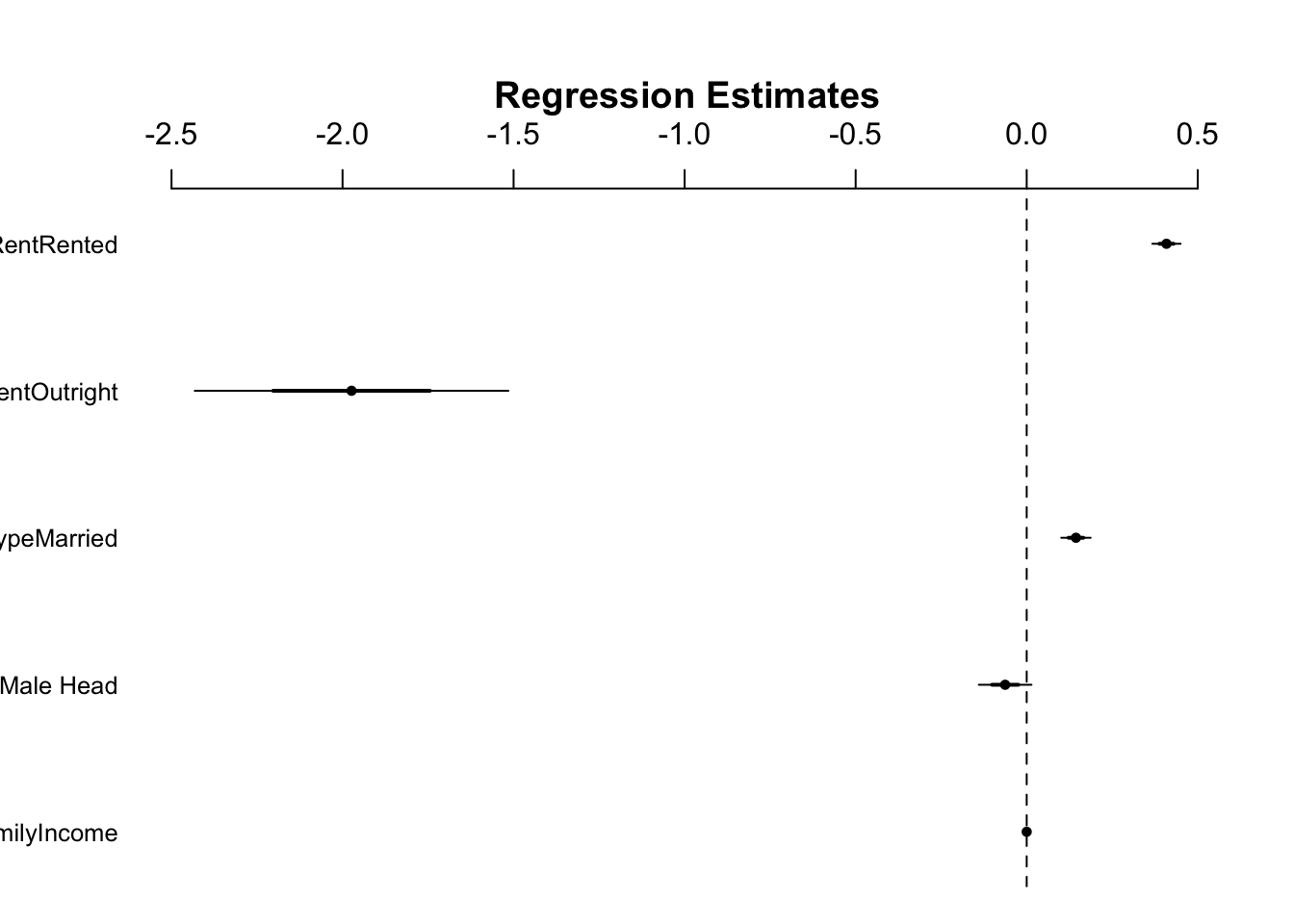
coefplot(children1)

¿Qué es la sobredisperción?

En estadística, la sobredispeción es la presencia de una mayor variabilidad (dispersión estadística) en un conjunto de datos de lo que se esperaría según un modelo estadístico dado. En el modelo Poisson, el promedio es igual a \(\lambda\) y la varianza es igual a \(\lambda\), entonces son iguales. Por consecuencia el supuesto es que la hipótesis nula es que la varianza es igual al promedio

OD = Overdispersion, Sobredisperción

La sobredispersión es definida como

\[OD=\frac { 1 }{ n-p } \sum _{ i=1 }^{ n }{ { z }_{ i }^{ 2 } }\]

donde

\[{ z }_{ i }=\frac { \gamma _{ i }-{ \hat { \gamma } }_{ i } }{ sd({ \hat { \gamma } }_{ i }) } =\frac { \gamma _{ i }-{ \mu }_{ i }{ \hat { \theta } }_{ i } }{ \sqrt { { \mu }_{ i }{ \hat { \theta } }_{ i } } }\]

Se puede evaluar los residuales estandarizados en R con el siguiente script o sea secuencia de comandos . El modelo se llama children1 y se aplica la formula arriba de la siguiente forma.

z<-(acs$NumChildren-children1$fitted.values)/sqrt(children1$fitted.values)
head(z)
##           1           2           3           4           5           6 
##  0.18186518  0.87627176 -0.84977889 -0.08314153  0.39096022  1.95966583

El factor/indice de sobredispersión

sum(z^2)/children1$df.residual
## [1] 1.469747

Probando si hay sobredisperión

Generalmente, una relación de sobredispersión de 2 o más indica sobredispersión. Si bien esta relación de sobredispersión es menor que 2, el valor p es 1, lo que significa que hay una sobredispersión estadísticamente significativa. Así que reajustamos el modelo para tener en cuenta la sobredispersión usando la familia de quasipoisson, que en realidad usa la distribución binomial negativa.

En paquete AER hay una función para evaluar la sobre dispersión que se llama dispersiontest

library(AER)
dispersiontest(children1, trafo=1)
## 
##  Overdispersion test
## 
## data:  children1
## z = 27.518, p-value < 2.2e-16
## alternative hypothesis: true alpha is greater than 0
## sample estimates:
##     alpha 
## 0.4696118

Pueden encontrar otras alternativas de como evaluar si hay sobre dispersión de los datos en este enlace. https://stats.stackexchange.com/questions/66586/is-there-a-test-to-determine-whether-glm-overdispersion-is-significant

children2<-glm(NumChildren~FamilyIncome+FamilyType+OwnRent,
               data=acs, family=quasipoisson(link="log"))

summary(children2)
## 
## Call:
## glm(formula = NumChildren ~ FamilyIncome + FamilyType + OwnRent, 
##     family = quasipoisson(link = "log"), data = acs)
## 
## Coefficients:
##                       Estimate Std. Error t value Pr(>|t|)    
## (Intercept)         -3.257e-01  2.549e-02 -12.777  < 2e-16 ***
## FamilyIncome         5.420e-07  7.968e-08   6.802 1.06e-11 ***
## FamilyTypeMale Head -6.298e-02  4.664e-02  -1.350    0.177    
## FamilyTypeMarried    1.440e-01  2.603e-02   5.532 3.20e-08 ***
## OwnRentOutright     -1.974e+00  2.779e-01  -7.102 1.27e-12 ***
## OwnRentRented        4.086e-01  2.506e-02  16.309  < 2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## (Dispersion parameter for quasipoisson family taken to be 1.469917)
## 
##     Null deviance: 35240  on 22744  degrees of freedom
## Residual deviance: 34643  on 22739  degrees of freedom
## AIC: NA
## 
## Number of Fisher Scoring iterations: 5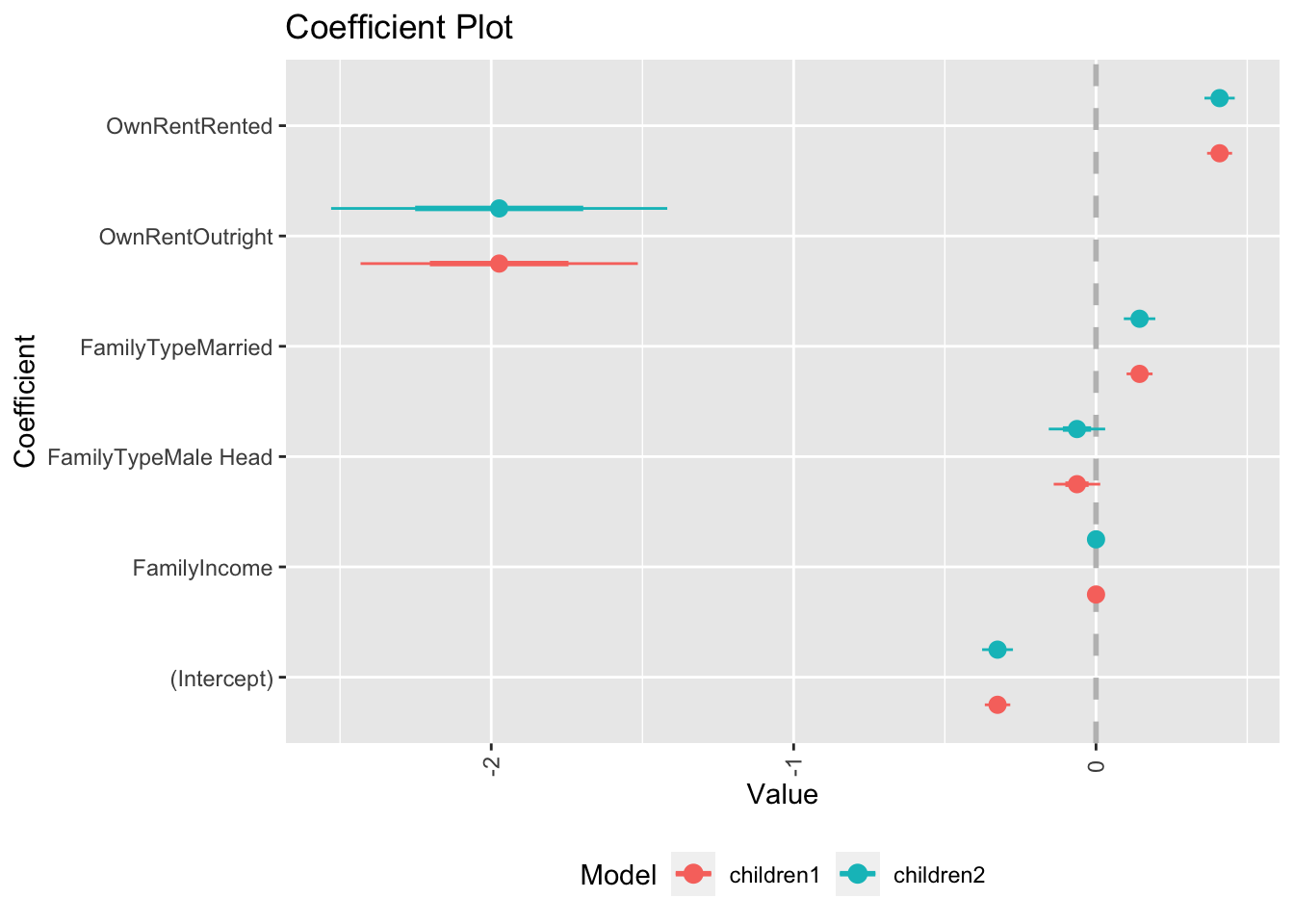
# Ahora se compara loa parámetros de los dos modelos  
multiplot(children1, children2)

“Activities reported in this website was supported by the National Institute of General Medical Sciences of the National Institutes of Health under Award Number R25GM121270. The content is solely the responsibility of the authors and does not necessarily represent the official views of the National Institutes of Health.”

`