Regresión Múltiple

Lista de paquetes a instalar

if (!require("pacman")) install.packages("pacman")
pacman::p_load(car, EnvStats,tidyverse, coefplot, leaps,
              rmarkdown, ggplot2, MASS, multcomp, effects, 
              gplots,agricolae, caret )


# Activar los paquetes
library(ggversa)
library(knitr)
library(tidyverse)
library(coefplot)
library(leaps)
library(EnvStats)
library(MASS)
library(car) # Companion to applied regression
library(ggplot2)  # Data Visualization
library(effects)
library(gplots)

Lista de archivos a usar

Los siguientes archivos deben estar disponible en su directorio de trabajo de R:

Objetivos Generales

Conocer y aplicar los métodos disponibles en R para obtener los parámetros de modelos de regresión múltiple, evaluar su idoneidad para describir los datos, e interpretar su significado.

Regresión Lineal Múltiple

Cuando tenemos más de una variable predictora (“independiente”), la regresión lineal simple es una regresión múltiple. El objetivo es simultaneamente evaluar múltiples variables independientes. La idea es de determinar cual impacto cada variable independiente tiene sobre la variable dependiente considerando que hay otras variables independientes.

La \(\alpha\) es el intercepto, las \(B_i\) son los coeficientes para cada variable independiente y el \(\epsilon\) es el error.

\[Y=\alpha+\beta_1X_{1}+\beta_2X_{2}+...+\beta_nX_{n}+\epsilon\]

Ejemplo 1 y Datos

Usaremos como ejemplo los datos bmi en el archivo mod_empiricos.xlsx. Estos son datos de individuos adultos entre 21 y 79 años, con las siguientes variables: BMI, un índice de masa corporal (\(kg/m^{2}\)); Age, edad (años); Cholesterol, niveles de colesterol en sangre, (\(mg/dL\)); Glucose, niveles de glucosa en la sangre, (\(mg/dL\)).

Para leer los datos emplearemos el siguiente código (obtenido del menú Import Dataset/From Excel): Nota que en este archivo de Excel hay más de una hoja de calculo, hay que indicar cual es la hoja que uno quiere importar usando sheet=“…”.

library(readxl)
reg.multiple <- read_excel("Data/mod_empiricos.xlsx", sheet = "bmi")
# para ver las primeras seis filas de datos
head(reg.multiple)

BMI	Age	Cholesterol	Glucose
19.3	21	178	95
24.5	57	250	98
24.7	46	176	102
47.9	47	171	105
44.2	61	222	101
29.9	74	156	72

Pruebas de supuestos para regresión múltiples

Cuando se utiliza regresión múltiple usando el método de mínimos cuadrados (OLS, ordinary least square), se asume que que cumple con los siguientes supuestos.

Normalidad:
- Gráficamente:
  - Q-Q plot;
- Estadísticamente:
  - prueba de Shapiro & Wilk (shapito.test)
  - Anderson-Darling (en el paquete nortest y la función ad_test).
Independencia: los valores de \(Y\) son independientes entre si, lo asumimos (no hay autocorrelación).
Linealidad: relación lineal entre variable dependiente y cada una de las independientes; gráficas individuales. Puede arreglarse con transformación; prueba de Box-Tidwell.
Homocedasticidad: varianza de la variable dependiente (residuales) no varía con los valores de las variables independientes; gráfica de los residuales.
Multicolinealidad: las variables independientes no deben estar correlacionadas entre si.

Normalidad

Evaluación gráfica de normalidad de la variable dependiente. Se observa que la mayoría de los datos son muy cerca de la linea, por consecuencia se puede asumir que la variable dependiente tiene una distribución normal.

ggplot(reg.multiple, aes(sample=BMI))+
  geom_qq()+
  geom_qq_line(colour="red")

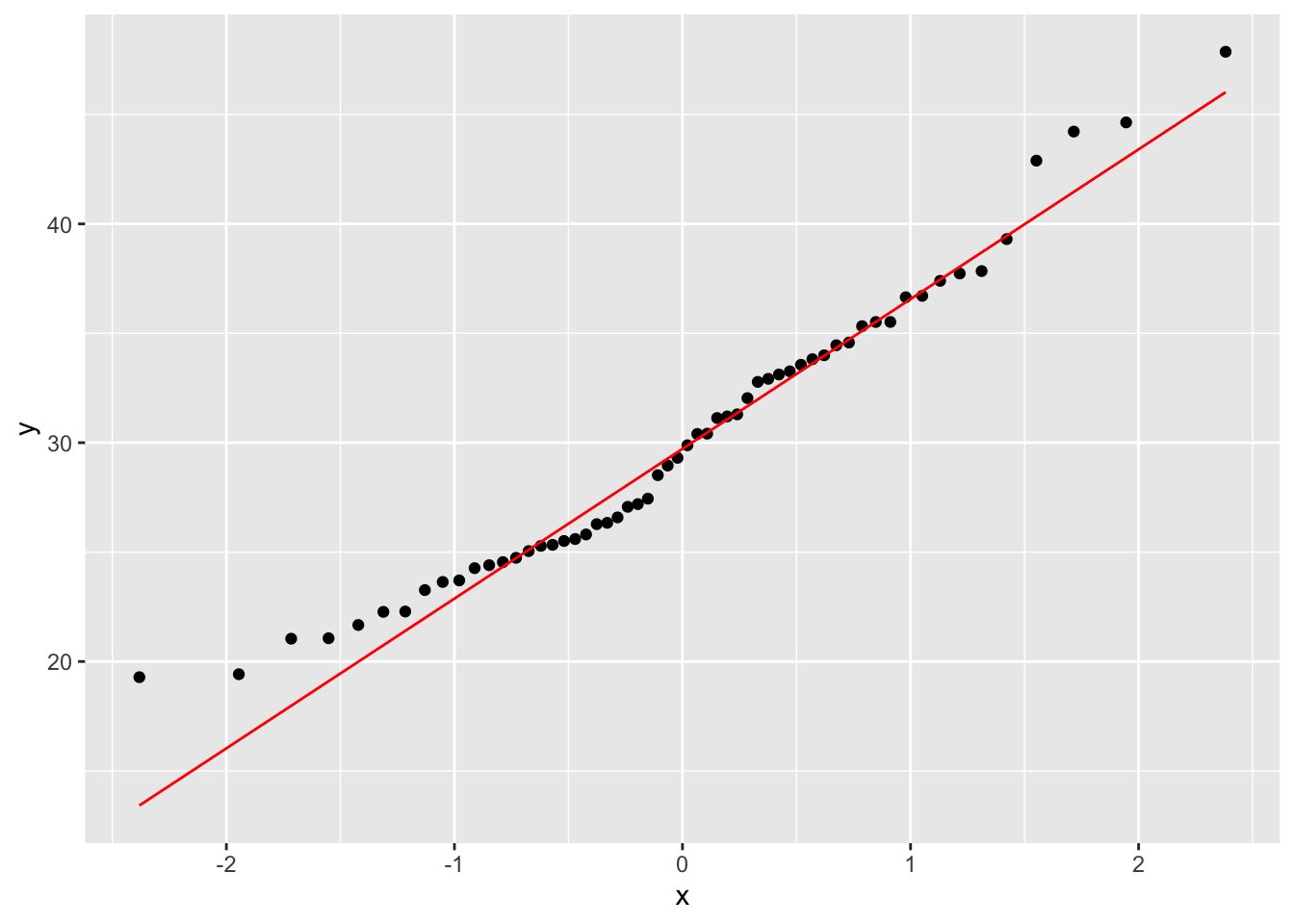
Pruebas de Normalidad

Prueba estadística de normalidad Shapiro & Wilk (\(H_0:distribución\enspace normal\)) . En este caso tanto la prueba de Shapiro_Wilk (p > 0.07) como la Anderson-Darling (p > 0.12) tienen el mismo resultado, que uno acepta la hipótesis nula, que no hay evidencia que los datos no provienen de una distribución normal.

shapiro.test(reg.multiple$BMI)

## 
##  Shapiro-Wilk normality test
## 
## data:  reg.multiple$BMI
## W = 0.96315, p-value = 0.07547

library(nortest)
ad.test(reg.multiple$BMI)

## 
##  Anderson-Darling normality test
## 
## data:  reg.multiple$BMI
## A = 0.58635, p-value = 0.1209

Prueba de Autocorrelación

La prueba de Durbin-Watson nos permite evaluar si ocurre autocorrelación entre los residuales de la variable dependiente. Por ejemplo, una variable que depende del tiempo, presenta autocorrelación. La \(H_0\) es que la autocorrelación en los residuales del modelo es 0.

Prueba de Durbin-Watson para autocorrelación.

Pasos:

Construir el modelo
Aplicar la prueba de autocorrelación sobre el modelo

La prueba de Durbin-Watson tiene un valor de p > 0.05, por consecuencia no hay evidencia que hay autocorrelación en los datos.

library(car)
model <- lm(BMI ~ Age + Cholesterol + Glucose, data = reg.multiple)
dbt <- durbinWatsonTest(model, simulate = TRUE)
dbt

##  lag Autocorrelation D-W Statistic p-value
##    1      0.06609505      1.823275   0.528
##  Alternative hypothesis: rho != 0

Prueba de linealidad del modelo

Prueba de Box Tidwell para linealidad. Esta prueba determina si el modelo sigue un patrón lineal. Los estimados de máxima verosimilitud de los parámetros de transformación se calculan mediante el método de Box y Tidwell (1962), que suele ser más eficaz que utilizar una rutina general de cuadrados mínimos no lineales (non linear least squares) para este problema. La hipótesis nula es que el patrón de relación entre las variables dependientes y indepedientes sean lineal.

Se observa que el valor de p >0.05 para cada variable sugiriendo que no hay evidencia que la relación sea diferente a una regresión lineal.

library(car)
boxTidwell(BMI ~ Age + Cholesterol + Glucose, data = reg.multiple)

##             MLE of lambda Score Statistic (t) Pr(>|t|)
## Age              -19.8117             -0.8984   0.3732
## Cholesterol       20.2797              0.1879   0.8517
## Glucose           -2.3134              0.1057   0.9162
## 
## iterations =  10 
## 
## Score test for null hypothesis that all lambdas = 1:
## F = 0.28618, df = 3 and 51, Pr(>F) = 0.8352

Prueba de multicolinealidad

Matriz de correlación con la correlaciones de Pearson (asume distribución normal) y gráficas de puntos con líneas de regresión. En este gráfico se observa que el patrón entre cada una de las variables independientes. Con esta se determina si hay alta colinearidad entre las variables.

La multicolinealidad se refiere a una situación en la que dos o más variables explicativas en un modelo de regresión múltiple están altamente relacionadas linealmente. Tenemos multicolinealidad perfecta si, por ejemplo, como en la ecuación anterior, la correlación entre dos variables independientes es igual a 1 o −1

Para dar un ejemplo sencillo si hubiesen dos variables con una correlación bien alta entre ambas, las dos variables incluyen un componente de variación compartido. Añadir las dos variables a un modelo de regresión múltiple no seria correcto, porque las dos variables explican la misma variación. En este caso lo que se observa es que BMI y el colesterol tiene una correlación de 28%.

library(car)
#matriz de correlación
signif(cor(reg.multiple),3)

##               BMI   Age Cholesterol Glucose
## BMI         1.000 0.186      0.2810  0.2210
## Age         0.186 1.000      0.1700  0.2670
## Cholesterol 0.281 0.170      1.0000  0.0827
## Glucose     0.221 0.267      0.0827  1.0000

Gráfica de regresiones en parejas, con línea de regresión

scatterplotMatrix(reg.multiple, ~ Age + Cholesterol + Glucose,
                  smooth = list(lty = 2), id = TRUE,
                  regLine = list(lty = 1, col = "red"),
                  col = "blue")

## Warning in applyDefaults(legend, defaults = list(coords = NULL, pt.cex = cex, :
## unnamed legend arguments, will be ignored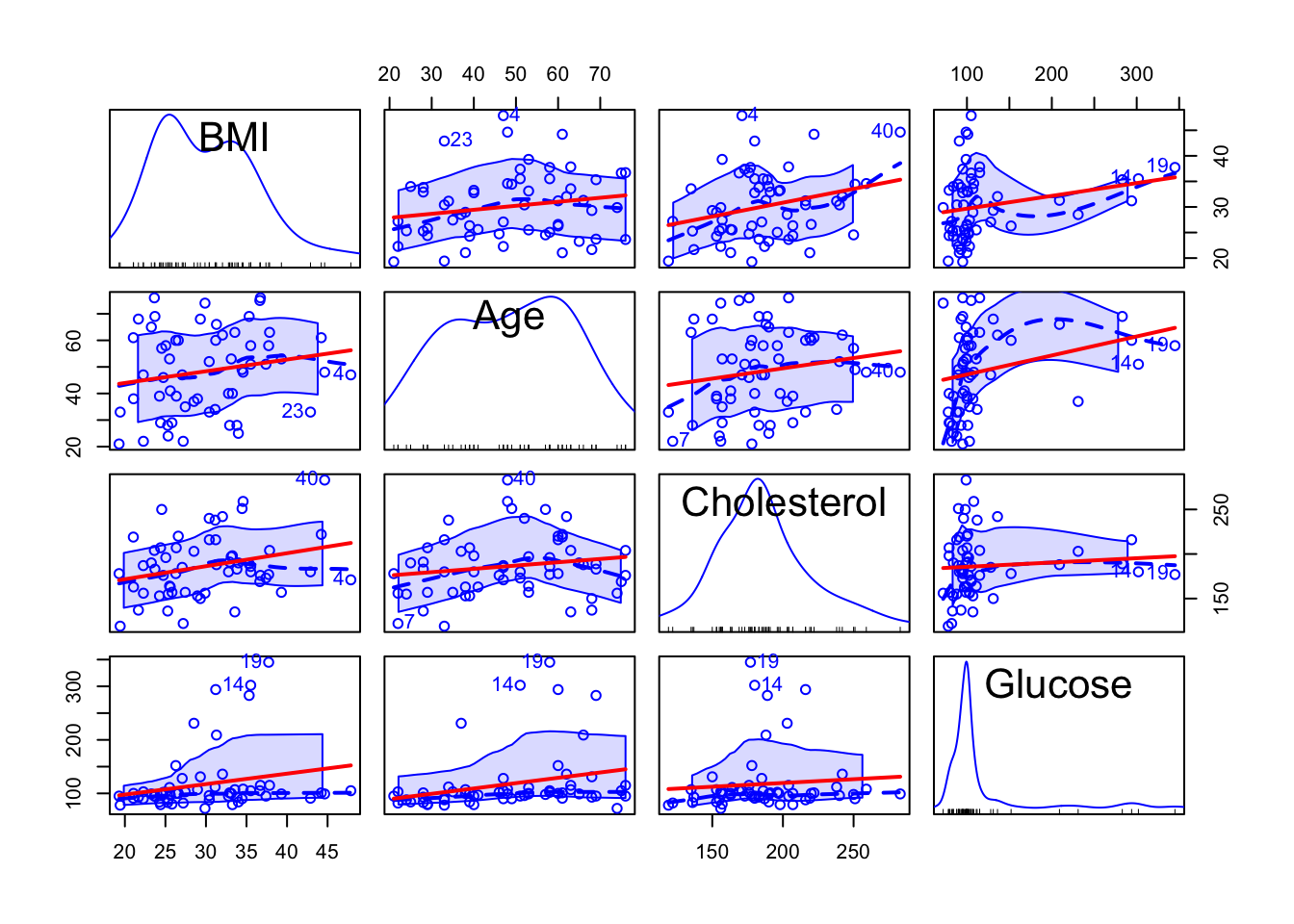

***

Prueba de Glauber para multicolinealidad

El paquete “mctest” en R proporciona la prueba de Farrar-Glauber y otras pruebas relevantes para la multicolinealidad. Hay dos funciones a saber. “Omcdiag” e “imcdiag” en el paquete “mctest” en R que proporcionarán la verificación de diagnóstico general e individual para la multicolinealidad, respectivamente.

library(mctest) # paquete para evaluar multicolinealidad
head(reg.multiple)

BMI	Age	Cholesterol	Glucose
19.3	21	178	95
24.5	57	250	98
24.7	46	176	102
47.9	47	171	105
44.2	61	222	101
29.9	74	156	72

model=lm(BMI ~ Age + Cholesterol + Glucose, data = reg.multiple)

omcdiag(model)

## 
## Call:
## omcdiag(mod = model)
## 
## 
## Overall Multicollinearity Diagnostics
## 
##                        MC Results detection
## Determinant |X'X|:         0.9006         0
## Farrar Chi-Square:         5.7786         0
## Red Indicator:             0.1888         0
## Sum of Lambda Inverse:     3.2125         0
## Theil's Method:           -0.0578         0
## Condition Number:         15.4471         0
## 
## 1 --> COLLINEARITY is detected by the test 
## 0 --> COLLINEARITY is not detected by the test

Determinar cual de las variables son correlacionados usar la función imcdiag. Encontrarán múltiples indices. Vemos el indice de VIF. Si ese valor es mayor de 10, se dice hay un alto nivel de correlación con esta variable.

Para detalles sobre los cálculos vea el siguiente enlace.

https://datascienceplus.com/multicollinearity-in-r/

imcdiag(model)

## 
## Call:
## imcdiag(mod = model)
## 
## 
## All Individual Multicollinearity Diagnostics Result
## 
##                VIF    TOL     Wi     Fi Leamer   CVIF Klein   IND1   IND2
## Age         1.1028 0.9067 2.8282 5.7592 0.9522 1.1497     0 0.0330 1.4252
## Cholesterol 1.0312 0.9697 0.8590 1.7492 0.9847 1.0751     0 0.0353 0.4629
## Glucose     1.0785 0.9272 2.1578 4.3940 0.9629 1.1243     0 0.0337 1.1119
## 
## 1 --> COLLINEARITY is detected by the test 
## 0 --> COLLINEARITY is not detected by the test
## 
## Age , Cholesterol , Glucose , coefficient(s) are non-significant may be due to multicollinearity
## 
## R-square of y on all x: 0.127 
## 
## * use method argument to check which regressors may be the reason of collinearity
## ===================================

Modelos de regresión lineal múltiple

A continuación se calculan los parámetros de diversos modelos de regresión, y se incluye una prueba de homocedasticidad (homogeneidad de la varianza) para cada modelo.

Modelo completo (todas las variables)

modRM <- lm(BMI ~ Age + Cholesterol + Glucose, 
              data = reg.multiple)
summary(modRM)

## 
## Call:
## lm(formula = BMI ~ Age + Cholesterol + Glucose, data = reg.multiple)
## 
## Residuals:
##      Min       1Q   Median       3Q      Max 
## -10.6255  -4.5473  -0.8179   3.7439  18.8116 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)   
## (Intercept) 16.81510    5.07180   3.315  0.00164 **
## Age          0.04103    0.05631   0.729  0.46939   
## Cholesterol  0.04819    0.02487   1.938  0.05791 . 
## Glucose      0.01974    0.01493   1.322  0.19188   
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 6.34 on 54 degrees of freedom
## Multiple R-squared:  0.127,  Adjusted R-squared:  0.07855 
## F-statistic:  2.62 on 3 and 54 DF,  p-value: 0.06008

aic <- AIC(modRM)
sprintf("AIC = %.2f", aic)

## [1] "AIC = 384.68"

# prueba de homocedasticidad (Non-constant Variance Score Test)
# Ho:la varianza es constante en el ámbito de la predicción de Y
ncvTest(modRM)  # para determinar si la varianza es constante. "Igualdad de varianza"

## Non-constant Variance Score Test 
## Variance formula: ~ fitted.values 
## Chisquare = 0.02932531, Df = 1, p = 0.86403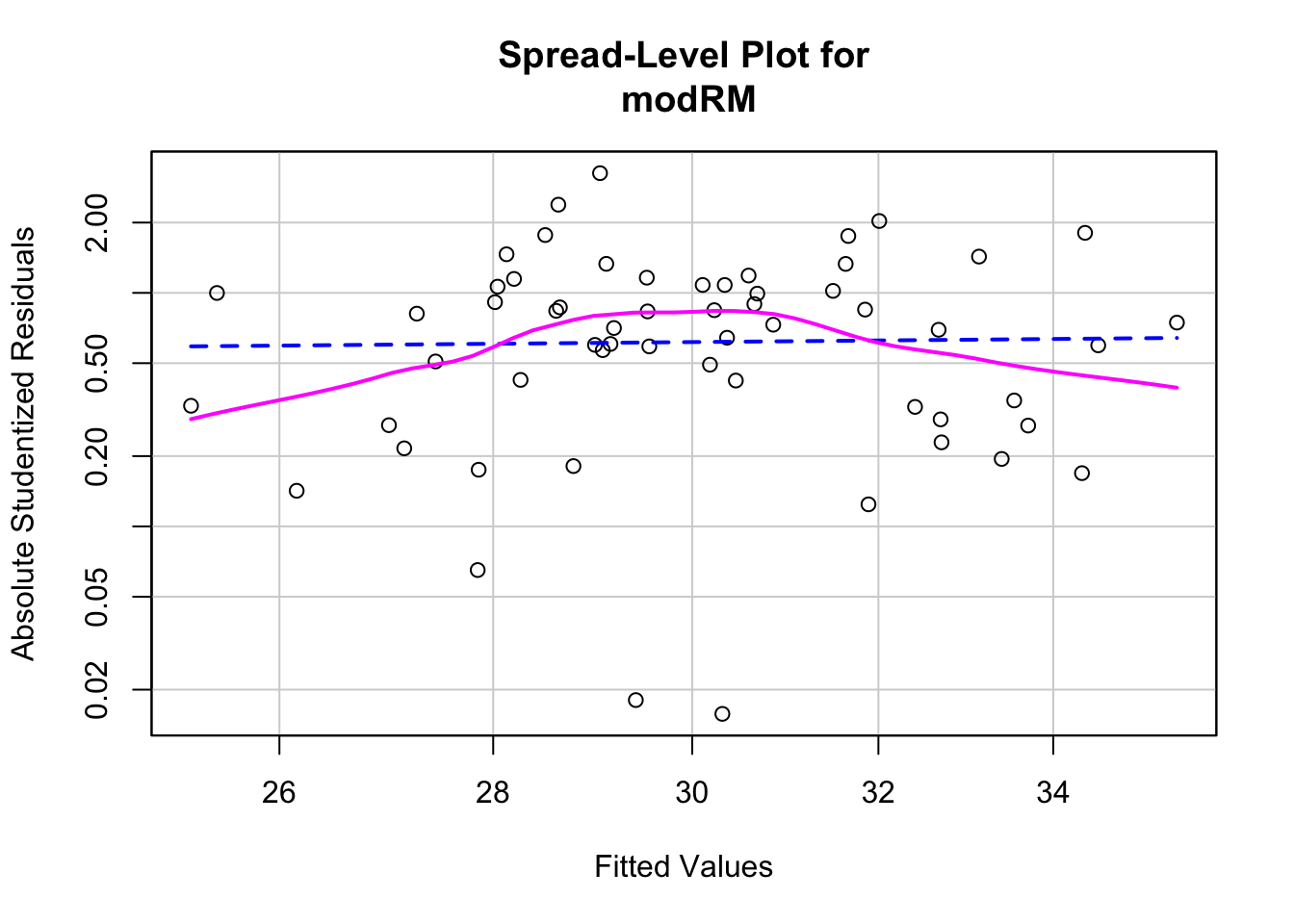

spreadLevelPlot(modRM)

## 
## Suggested power transformation:  0.757141

Modelo eliminando la variable Age, por ser la menos correlaciona con BMI, y tener la mayor correlación con Glucose

modRM <- lm(BMI ~ Cholesterol + Glucose, 
              data = reg.multiple)
summary(modRM)

## 
## Call:
## lm(formula = BMI ~ Cholesterol + Glucose, data = reg.multiple)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -10.125  -4.748  -1.134   3.321  18.832 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept) 17.95236    4.80502   3.736 0.000446 ***
## Cholesterol  0.05098    0.02447   2.083 0.041902 *  
## Glucose      0.02254    0.01437   1.569 0.122449    
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 6.313 on 55 degrees of freedom
## Multiple R-squared:  0.1185, Adjusted R-squared:  0.08641 
## F-statistic: 3.696 on 2 and 55 DF,  p-value: 0.0312

aic <- AIC(modRM)
sprintf("AIC = %.2f", aic)

## [1] "AIC = 383.25"

# prueba de homocedasticidad
ncvTest(modRM)

## Non-constant Variance Score Test 
## Variance formula: ~ fitted.values 
## Chisquare = 0.2490362, Df = 1, p = 0.61775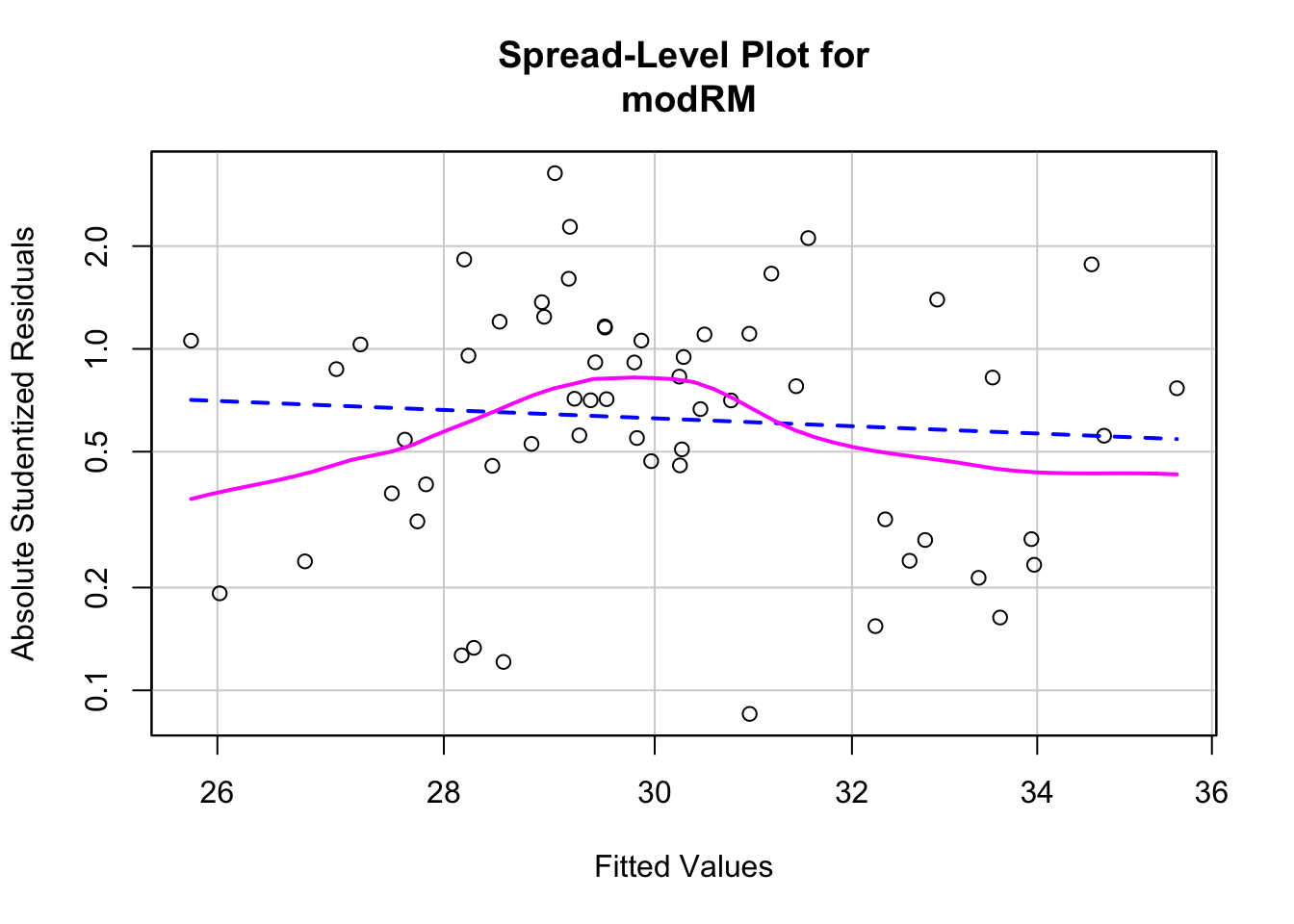

spreadLevelPlot(modRM)

## 
## Suggested power transformation:  1.818741

Modelo con interacción entre Age y Glucose

Para denotar interacción entre variables se usa el símbolo ( : ) Para incluir las variables solas y su interacción se utiliza el símbolo ( * )

modRM <- lm(BMI ~ Cholesterol + Glucose:Age, 
              data = reg.multiple)
summary(modRM)

## 
## Call:
## lm(formula = BMI ~ Cholesterol + Glucose:Age, data = reg.multiple)
## 
## Residuals:
##      Min       1Q   Median       3Q      Max 
## -10.5225  -4.6283  -0.8796   3.6945  18.8840 
## 
## Coefficients:
##              Estimate Std. Error t value Pr(>|t|)    
## (Intercept) 1.879e+01  4.645e+00   4.044 0.000165 ***
## Cholesterol 4.906e-02  2.441e-02   2.010 0.049322 *  
## Glucose:Age 3.662e-04  2.057e-04   1.780 0.080625 .  
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 6.274 on 55 degrees of freedom
## Multiple R-squared:  0.1292, Adjusted R-squared:  0.09751 
## F-statistic: 4.079 on 2 and 55 DF,  p-value: 0.02229

aic <- AIC(modRM)
sprintf("AIC = %.2f", aic)

## [1] "AIC = 382.54"

# prueba de homocedasticidad
ncvTest(modRM)

## Non-constant Variance Score Test 
## Variance formula: ~ fitted.values 
## Chisquare = 0.07666205, Df = 1, p = 0.78187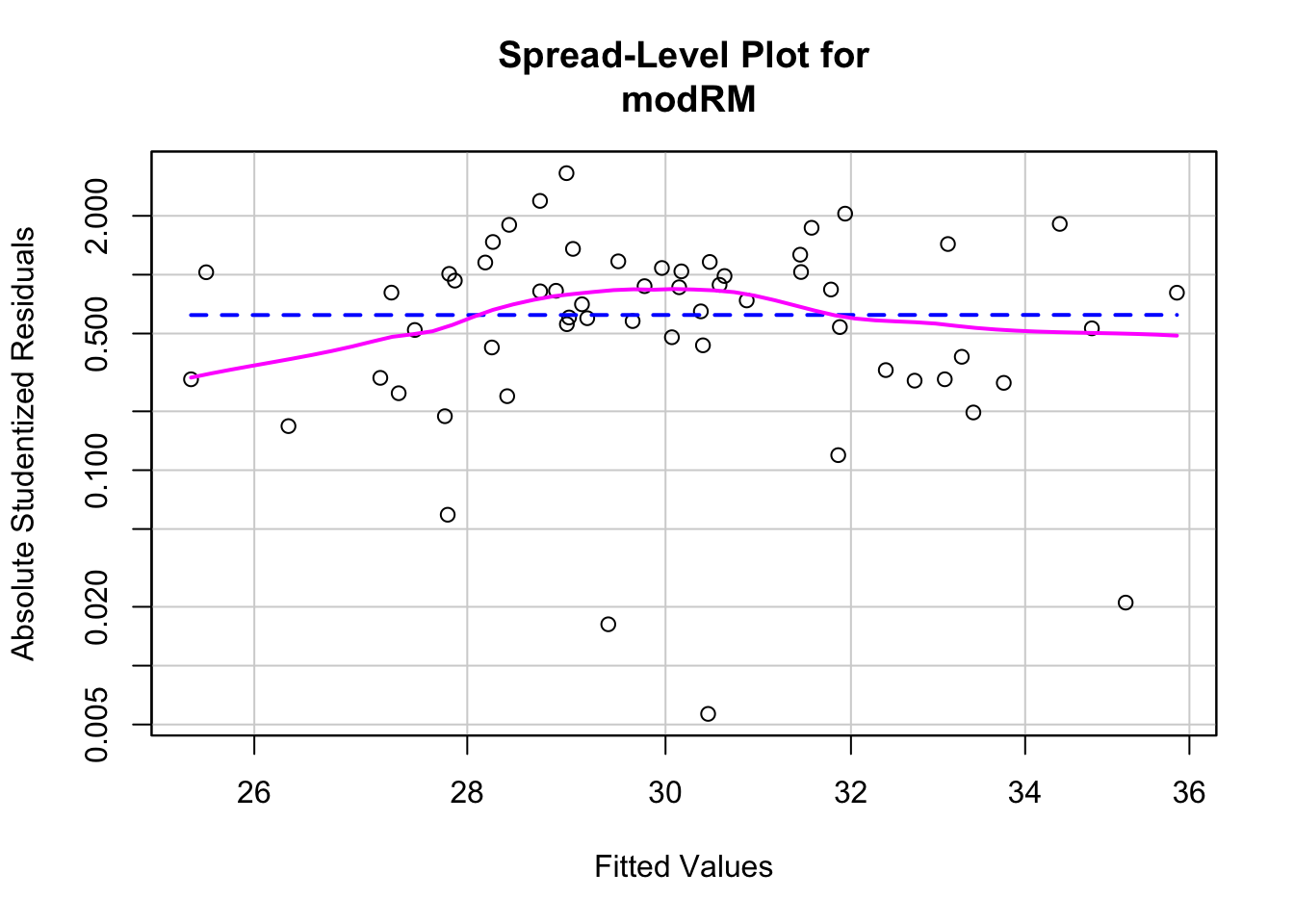

spreadLevelPlot(modRM)

## 
## Suggested power transformation:  0.9950719

Selección automática de modelo - método “stepwise”

Existen métodos para seleccionar automáticamente el mejor modelo, a base de estadísticas indicadoras, y que conlleva un procedimiento iterativo. Uno de estos procedimientos es conocido como ‘stepwise’ (por pasos), y aunque no es el más aceptado en la actualidad, ha sido muy usado y es una buena manera de ilustrar el procedimiento.

En este procedimiento el proceso de selección se basa en seleccionar el modelo que minimiza el valor de la estadística AIC (Akaike Information Criterion), que indica el modelo con la menor pérdida de información y mayor simplicidad. En el proceso se parte de un modelo nulo (no efecto de predictores) y hasta un modelo muy complejo, incluyendo interacciones. Las variables se incluyen y se quitan, y cada vez se recalcula AIC, hasta obtener el modelo que mantiene el mínimo valor de AIC.

#formulación de un modelo nulo y un modelo completo
modNulo <- lm(BMI ~ 1, data = reg.multiple)
modFull <- lm(BMI ~ Cholesterol*Glucose + Age*Cholesterol + Age*Glucose, 
              data = reg.multiple)
#procedimiento stepwise
bmistep <- step(modNulo,
                scope = list(lower=modNulo, upper=modFull,
                             direction="both"))

## Start:  AIC=219.97
## BMI ~ 1
## 
##               Df Sum of Sq    RSS    AIC
## + Cholesterol  1   196.462 2289.8 217.19
## + Glucose      1   121.605 2364.6 219.06
## + Age          1    86.322 2399.9 219.92
## <none>                     2486.2 219.97
## 
## Step:  AIC=217.19
## BMI ~ Cholesterol
## 
##               Df Sum of Sq    RSS    AIC
## + Glucose      1    98.063 2191.7 216.66
## <none>                     2289.8 217.19
## + Age          1    49.203 2240.6 217.93
## - Cholesterol  1   196.462 2486.2 219.97
## 
## Step:  AIC=216.66
## BMI ~ Cholesterol + Glucose
## 
##                       Df Sum of Sq    RSS    AIC
## <none>                             2191.7 216.66
## + Cholesterol:Glucose  1    55.387 2136.3 217.17
## - Glucose              1    98.063 2289.8 217.19
## + Age                  1    21.337 2170.3 218.09
## - Cholesterol          1   172.920 2364.6 219.06

summary(bmistep)

## 
## Call:
## lm(formula = BMI ~ Cholesterol + Glucose, data = reg.multiple)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -10.125  -4.748  -1.134   3.321  18.832 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept) 17.95236    4.80502   3.736 0.000446 ***
## Cholesterol  0.05098    0.02447   2.083 0.041902 *  
## Glucose      0.02254    0.01437   1.569 0.122449    
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 6.313 on 55 degrees of freedom
## Multiple R-squared:  0.1185, Adjusted R-squared:  0.08641 
## F-statistic: 3.696 on 2 and 55 DF,  p-value: 0.0312

Comparación de modelos

Gráfica de coeficientes

Una manera de comparar modelos visualmente (en realidad sus coeficientes) es usar el paquete coefplot, en conjunto con ggplot2, para crear una gráfica de los coeficientes estimados de cada variable (sola o de interacción), en cada modelo y detectar los que son diferentes de 0, y los modelos que los contienen.

library(ggplot2)
library(coefplot)
#cálculo para todos los modelos
modbmi1 <- lm(BMI ~ Age + Cholesterol + Glucose, data=reg.multiple)
modbmi2 <- lm(BMI ~ Age*Glucose + Cholesterol*Glucose + Age*Cholesterol, data=reg.multiple)
modbmi3 <- lm(BMI ~ Cholesterol + Age:Glucose, data=reg.multiple)
modbmi4 <- lm(BMI ~ Cholesterol + Glucose, data=reg.multiple)
modbmi5 <- lm(BMI ~ Cholesterol, data = reg.multiple)
#comparando coeficientes de todos los modelos
multiplot(modbmi1, modbmi2, modbmi3, modbmi4, modbmi5, pointSize = 2, intercept=FALSE)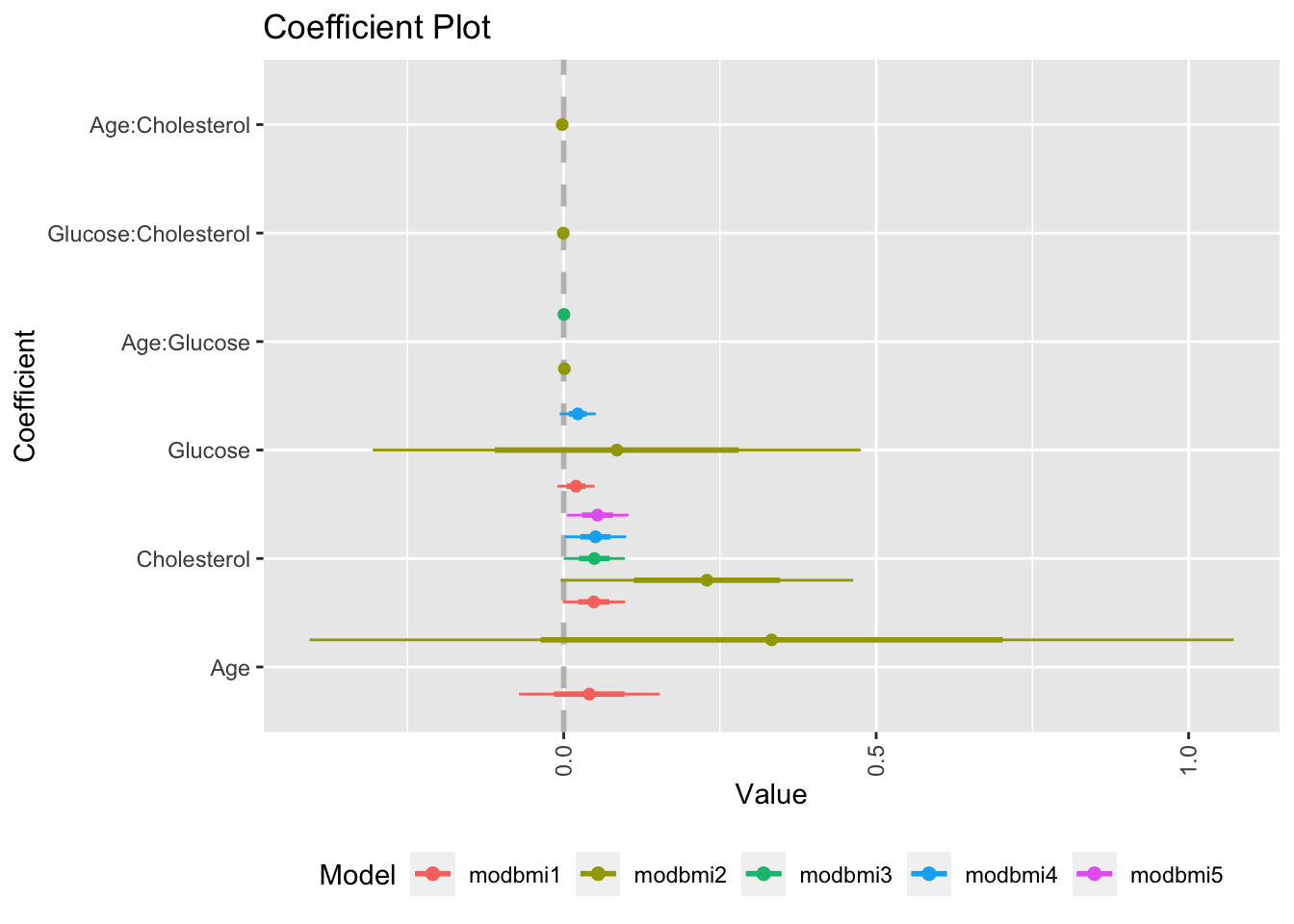

Selección de modelo usando R-cuadrado ajustado y Mallow’s Cp para mejores modelos

La estadística \(R^2\) es la cantidad de varianza en la respuesta (variable dependiente) producida por las variables predictoras, mediante el modelo, por lo tanto constituye una buena manera de medir la capacidad del modelo para “explicar” los datos. Sin embargo, en un modelo de regresión múltiple, el \(R^2\) aumenta al aumentar el número de predictores, lo cual conlleva a sobrestimar la “calidad” del modelo, con un número excesivo de variables. Usando el \(R^2\) ajustado se toma en cuenta el número de parámetros en el modelo, por lo tanto es una medida más realista del ajuste al modelo.

La estadística de Mallow, \(C_p\), es otro indicador para seleccionar el mejor modelo en una regresión múltiple; funciona de manera similar al AIC, y sirve para evitar incluir parámetros en exceso. La regla general es escoger el modelo con el número de parámetros, en el cual el valor de \(C_p\) sea cercano (pero menor) al número de parámetros más 1.

library(leaps)
modSS <- regsubsets(BMI ~ Age*Cholesterol + Cholesterol*Glucose + Age*Glucose, data = reg.multiple, nbest = 3, intercept = TRUE)
# gráfica para R^2 ajustado
plot(modSS, scale="adjr2")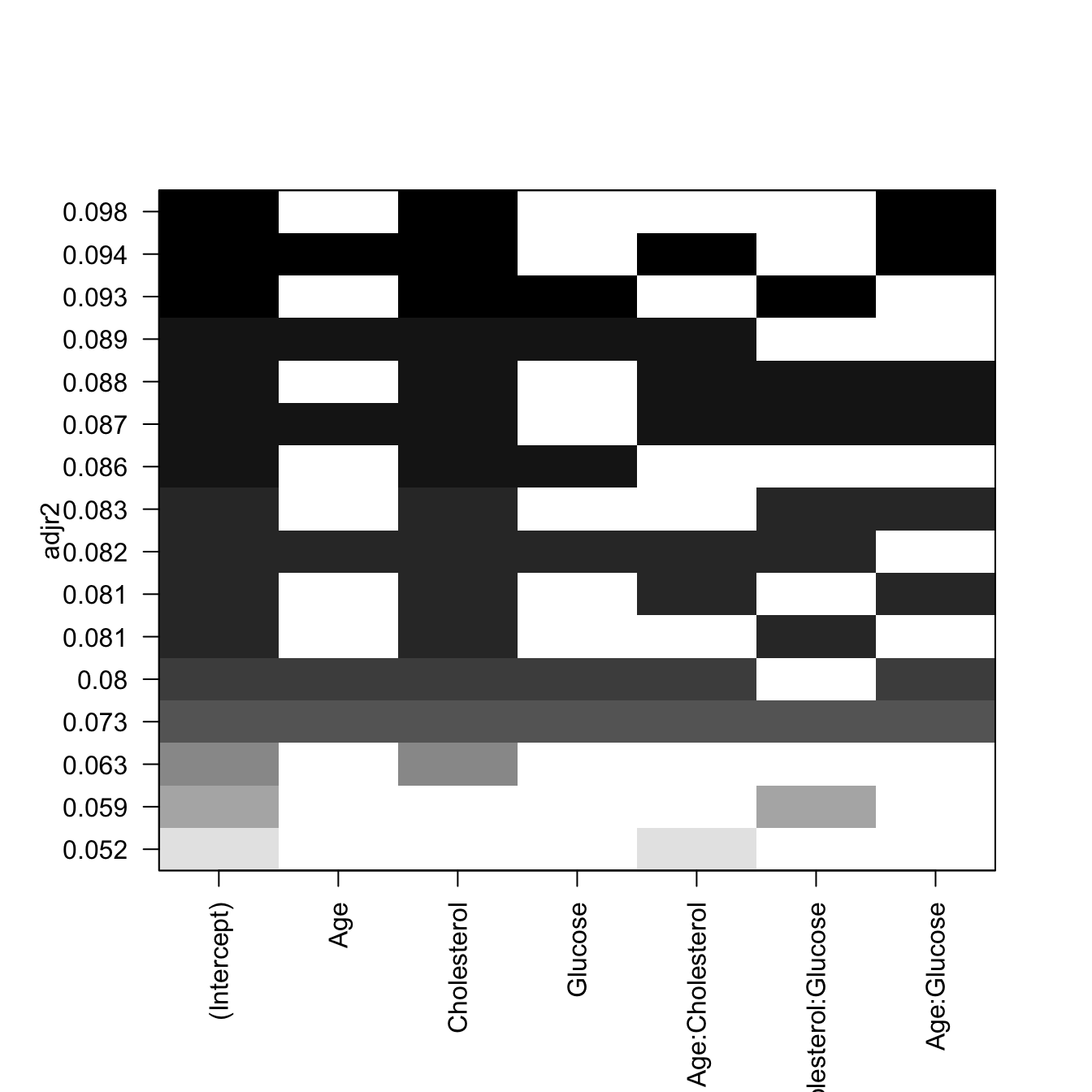

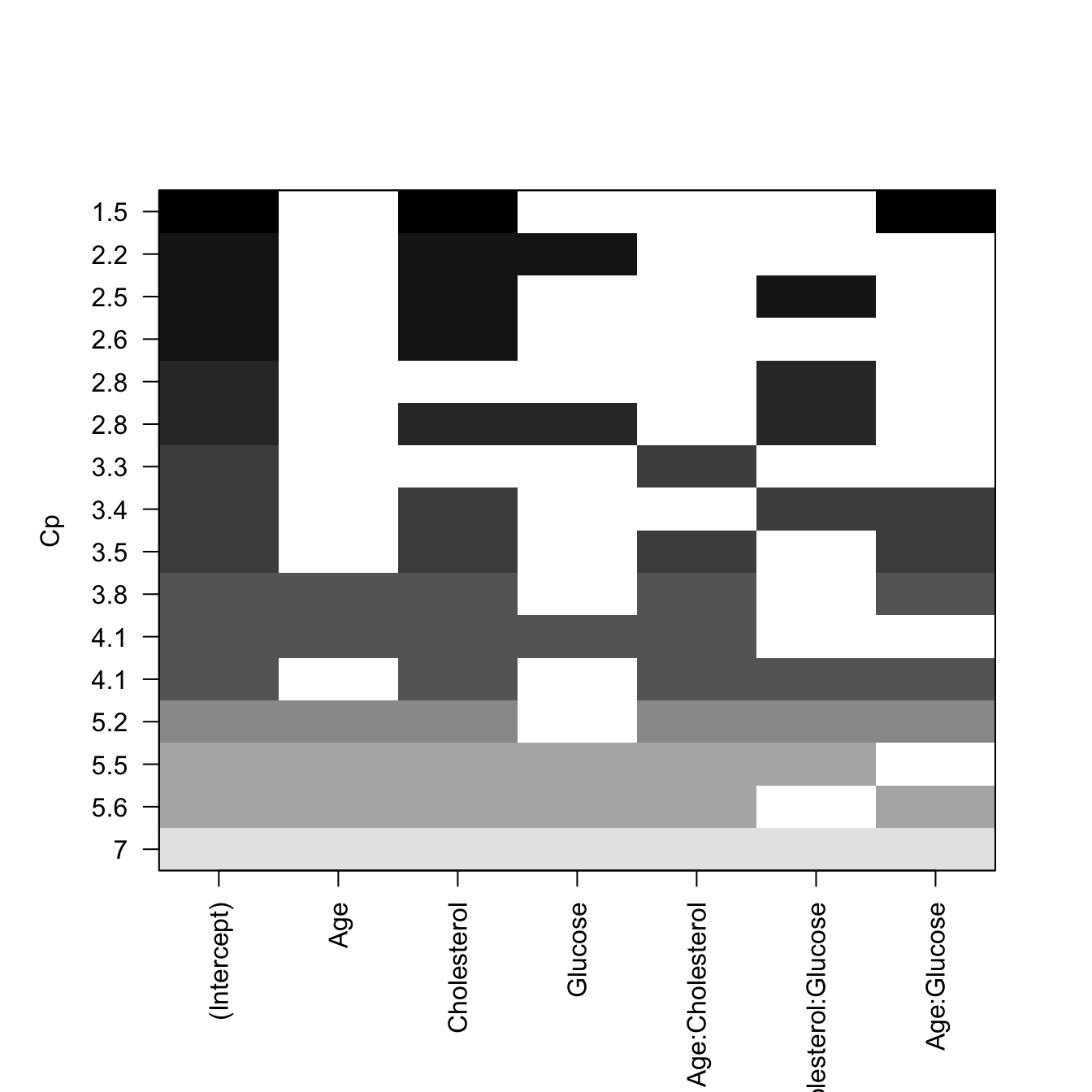
# gráfica para Cp
plot(modSS, scale="Cp")

# otra forma de visualizar Cp
library(car)
## Mallow Cp
mallowCp <-
    subsets(modSS, statistic="cp", legend = FALSE, min.size = 1, main = "Mallow Cp")
abline(a = 1, b = 1, lty = 2)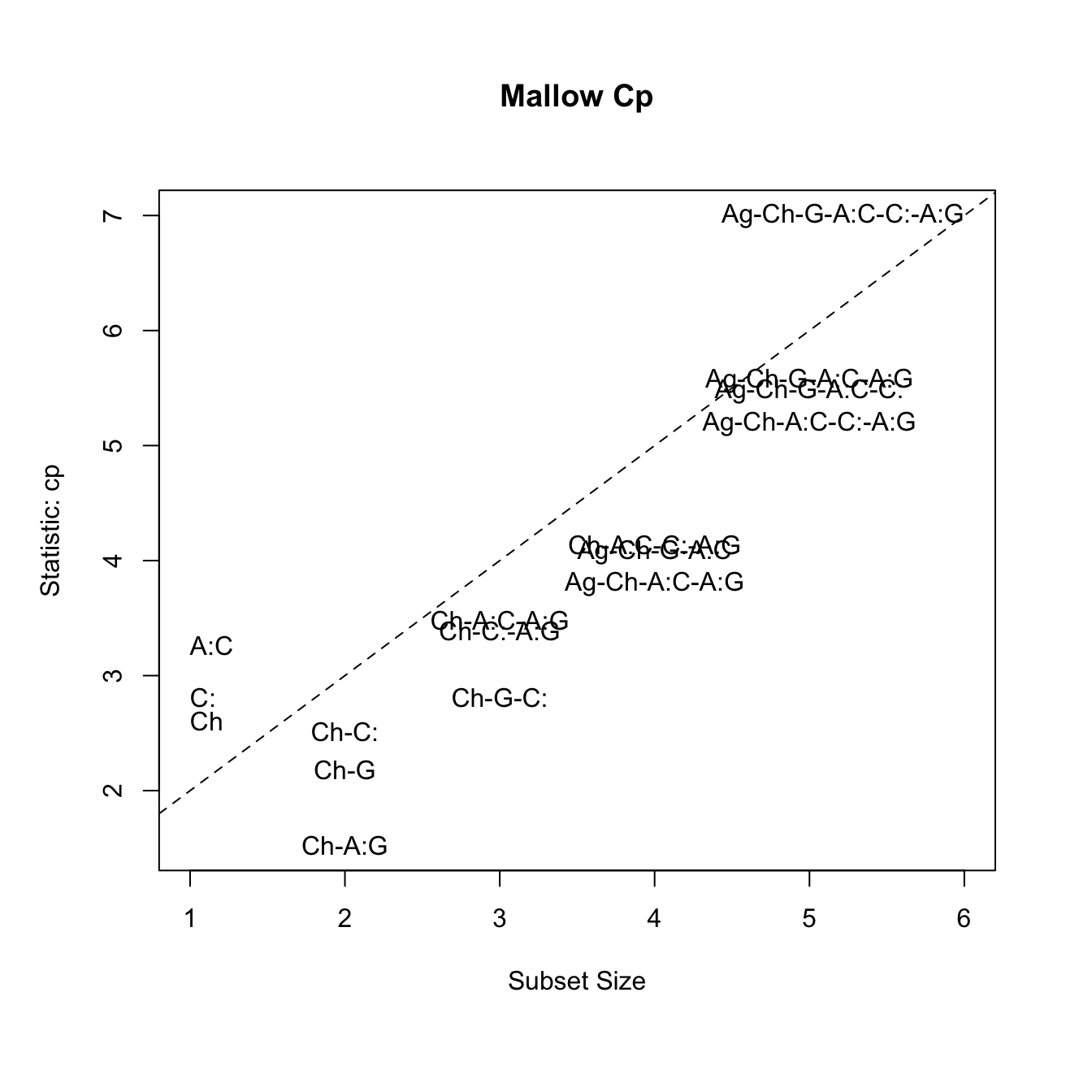

EJERCICIO

Usar los datos deathsmall_cities.xlsx para buscar un modelo de regresión múltiple entre la variable dependiente death1K (muertes anuales por cada 1000 habitantes) y las otras variables del archivo.

library(readxl)
death_small_cities <- read_excel("Data/death_small_cities.xlsx", sheet=2)
dsc=death_small_cities
head(dsc)

death1K	doctor100K	hosp100K	income1K	density
8	78	284	9.1	109
9.3	68	433	8.7	144
7.5	70	739	7.2	113
8.9	96	1.79e+03	8.9	97
10.2	74	477	8.3	206
8.3	111	362	10.9	124

Normalidad

Visualización

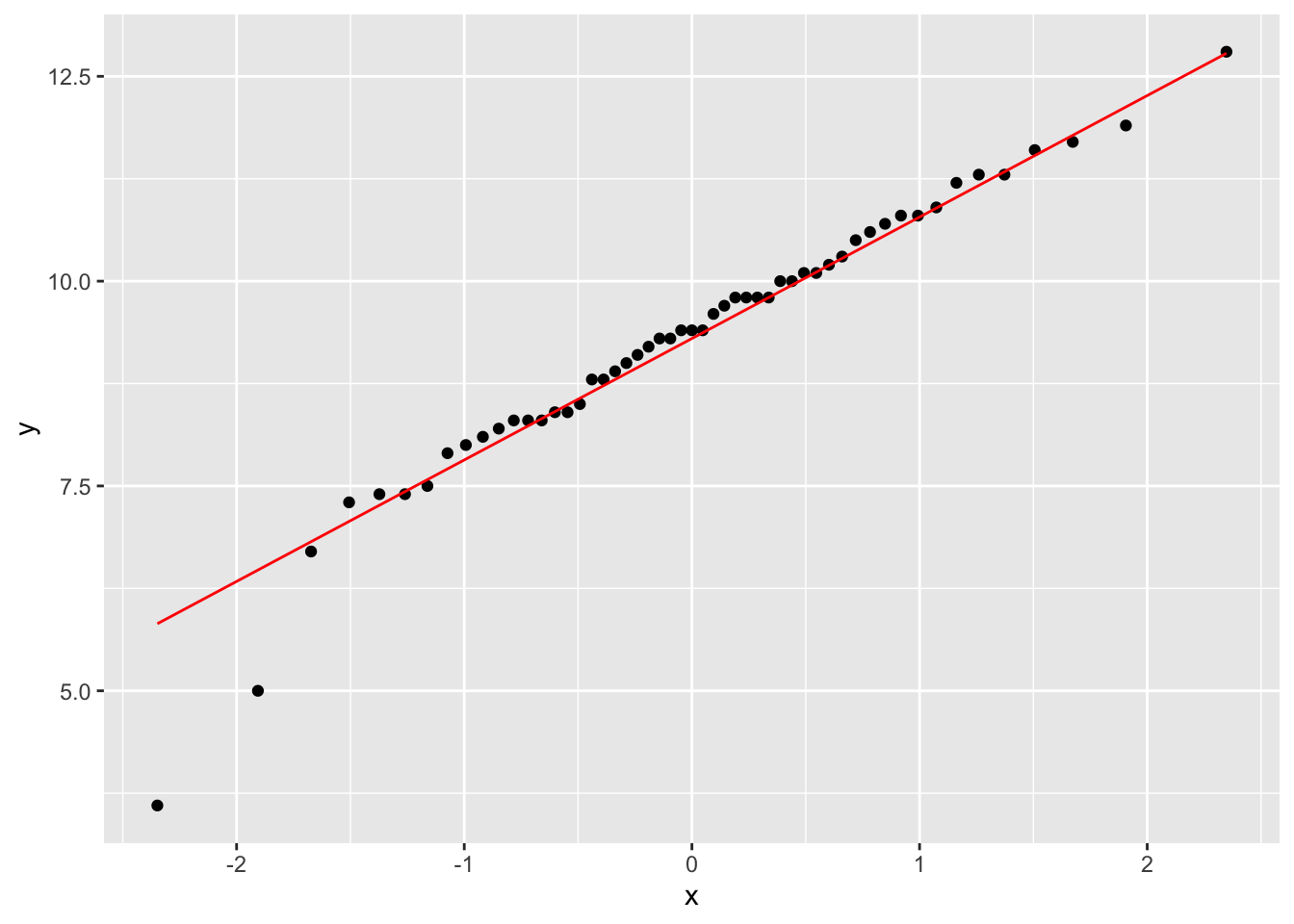
Pruebas

## 
##  Shapiro-Wilk normality test
## 
## data:  dsc$death1K
## W = 0.95746, p-value = 0.05679

## 
##  Anderson-Darling normality test
## 
## data:  dsc$death1K
## A = 0.44143, p-value = 0.279

Prueb a de autocorelación de Durbin Watson

## [1] "death1K"    "doctor100K" "hosp100K"   "income1K"   "density"

##  lag Autocorrelation D-W Statistic p-value
##    1        0.170017      1.589951   0.134
##  Alternative hypothesis: rho != 0

Multicolienarity

##            death1K doctor100K hosp100K income1K density
## death1K      1.000     0.1160   0.1110  -0.1720 -0.2780
## doctor100K   0.116     1.0000   0.2960   0.4330 -0.0199
## hosp100K     0.111     0.2960   1.0000   0.0275  0.1870
## income1K    -0.172     0.4330   0.0275   1.0000  0.1290
## density     -0.278    -0.0199   0.1870   0.1290  1.0000

Visualizando colinearidad

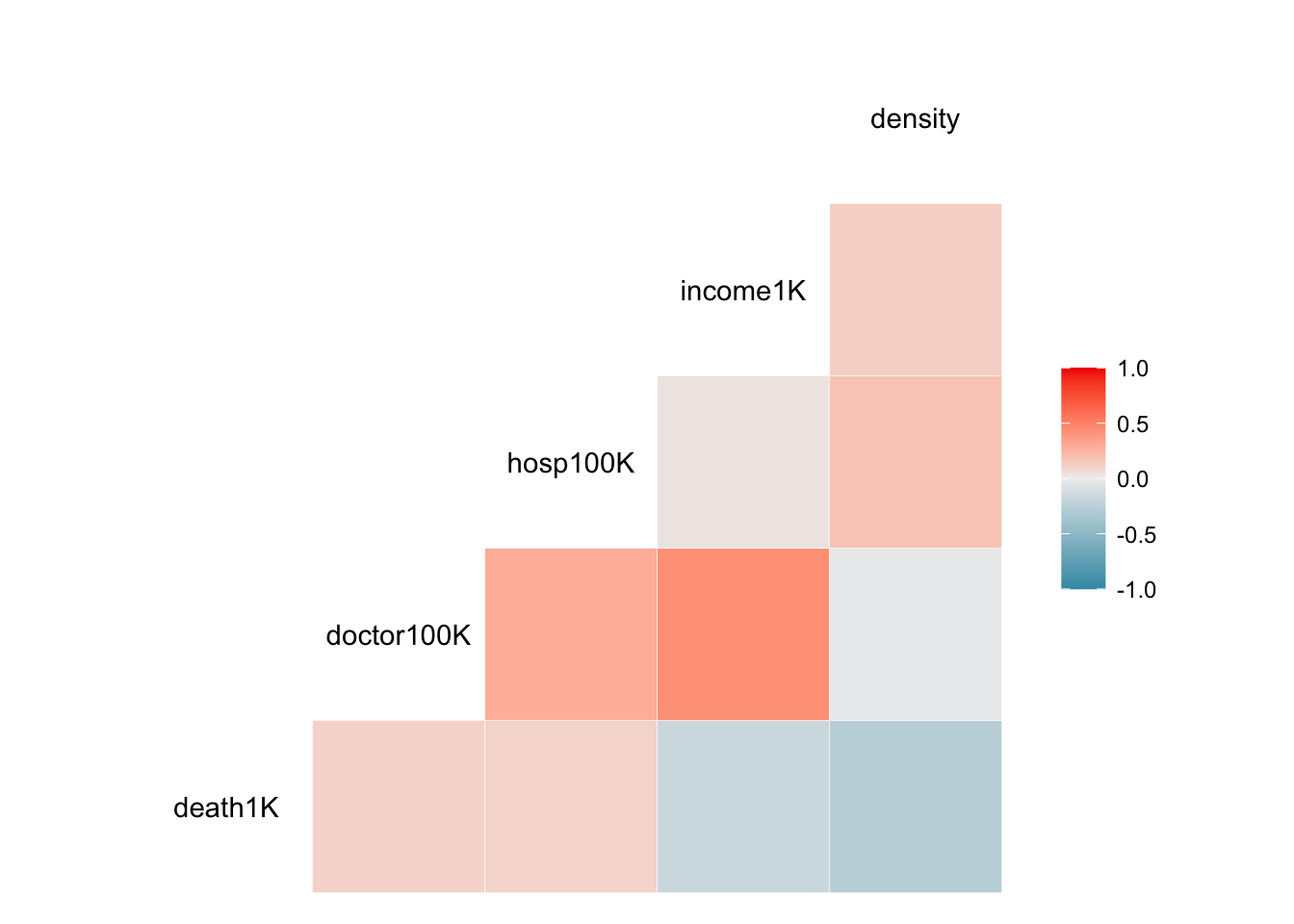
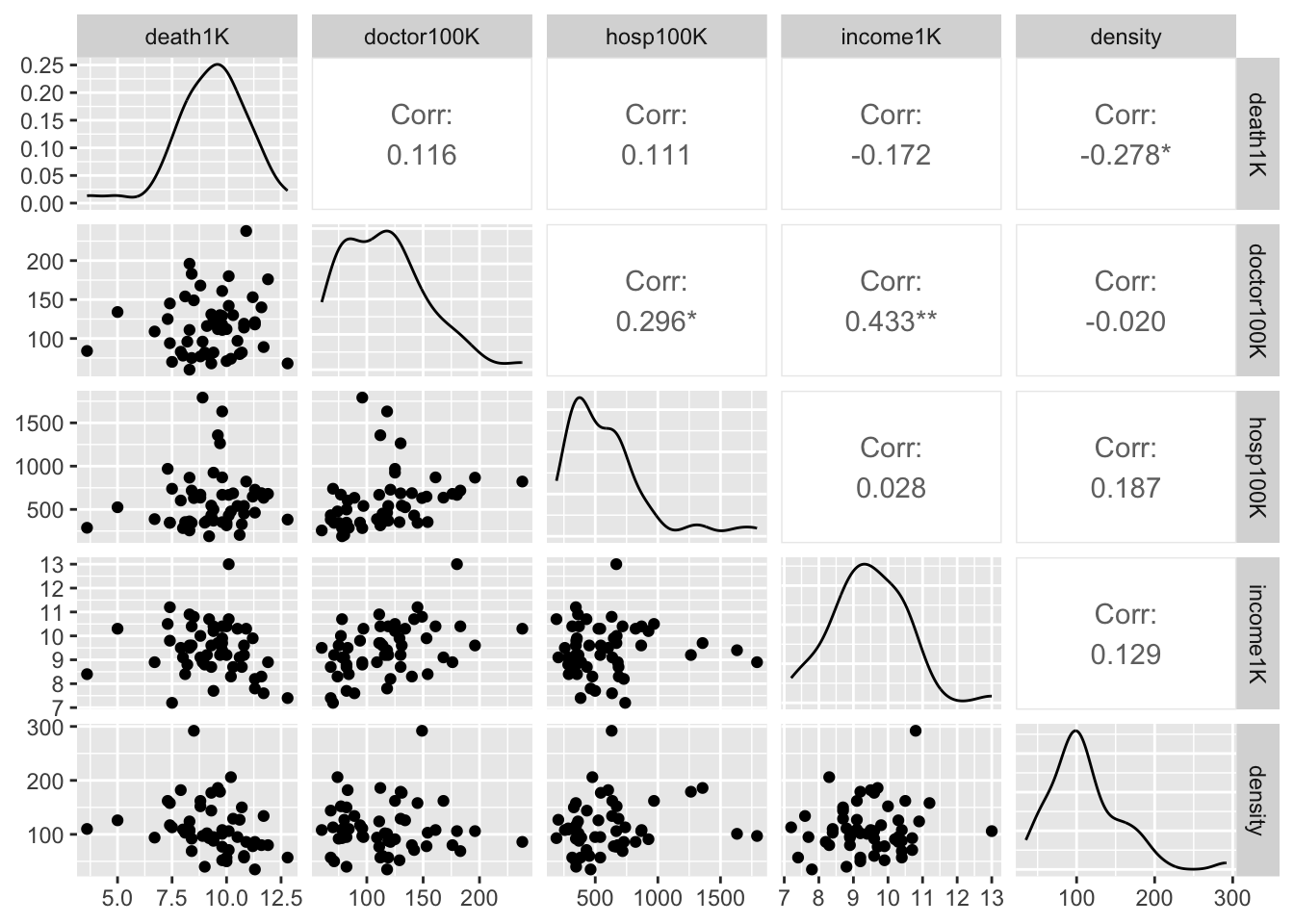
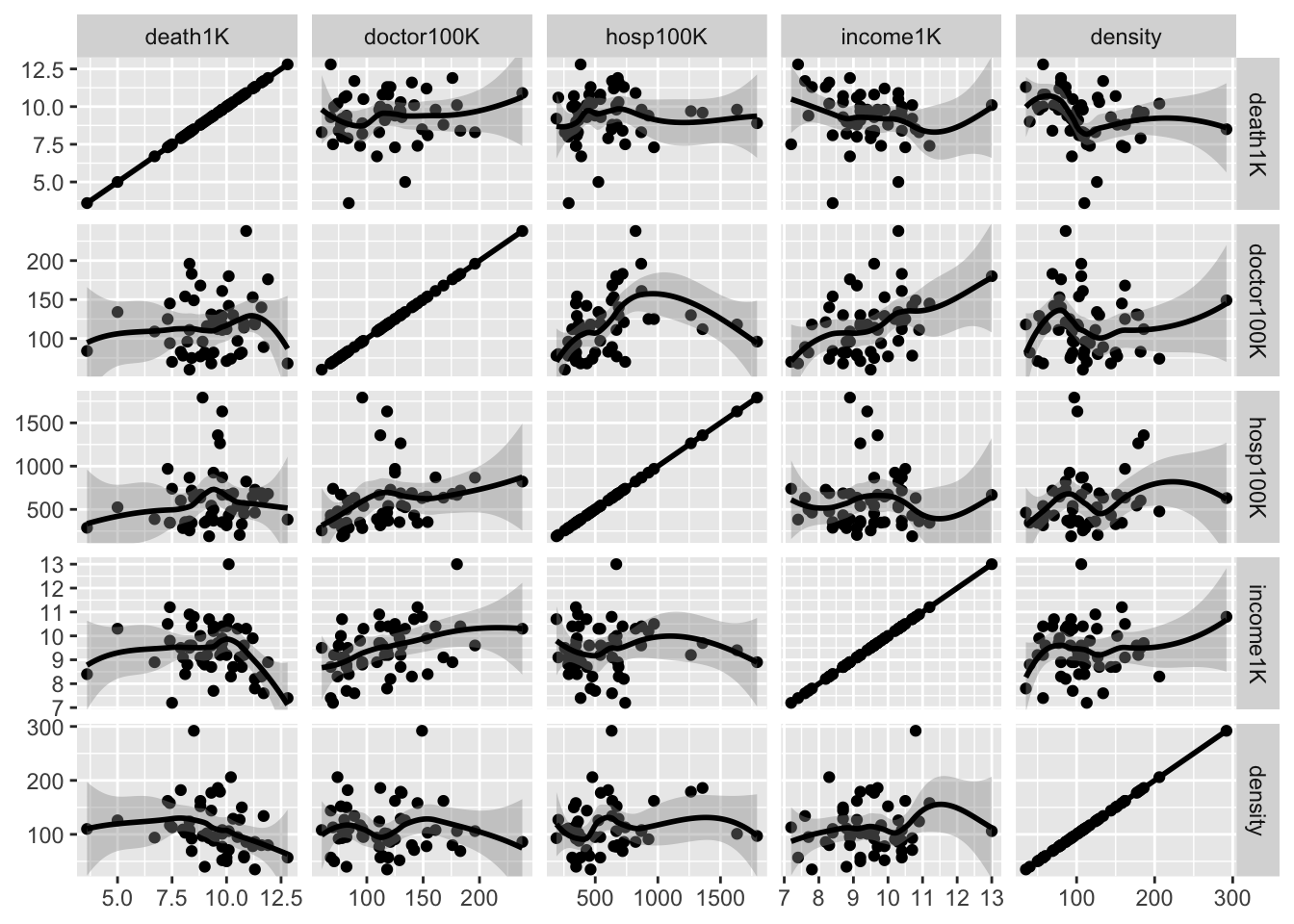
El Modelo

## 
## Call:
## lm(formula = death1K ~ doctor100K + hosp100K + income1K + density, 
##     data = dsc)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -5.6404 -0.7904  0.3053  0.9164  2.7906 
## 
## Coefficients:
##               Estimate Std. Error t value Pr(>|t|)    
## (Intercept) 12.2662552  2.0201467   6.072 1.95e-07 ***
## doctor100K   0.0073916  0.0069336   1.066   0.2917    
## hosp100K     0.0005837  0.0007219   0.809   0.4228    
## income1K    -0.3302302  0.2345518  -1.408   0.1656    
## density     -0.0094629  0.0048868  -1.936   0.0587 .  
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 1.601 on 48 degrees of freedom
## Multiple R-squared:  0.1437, Adjusted R-squared:  0.07235 
## F-statistic: 2.014 on 4 and 48 DF,  p-value: 0.1075

## [1] "AIC = 207.06"

## Non-constant Variance Score Test 
## Variance formula: ~ fitted.values 
## Chisquare = 0.04184651, Df = 1, p = 0.83791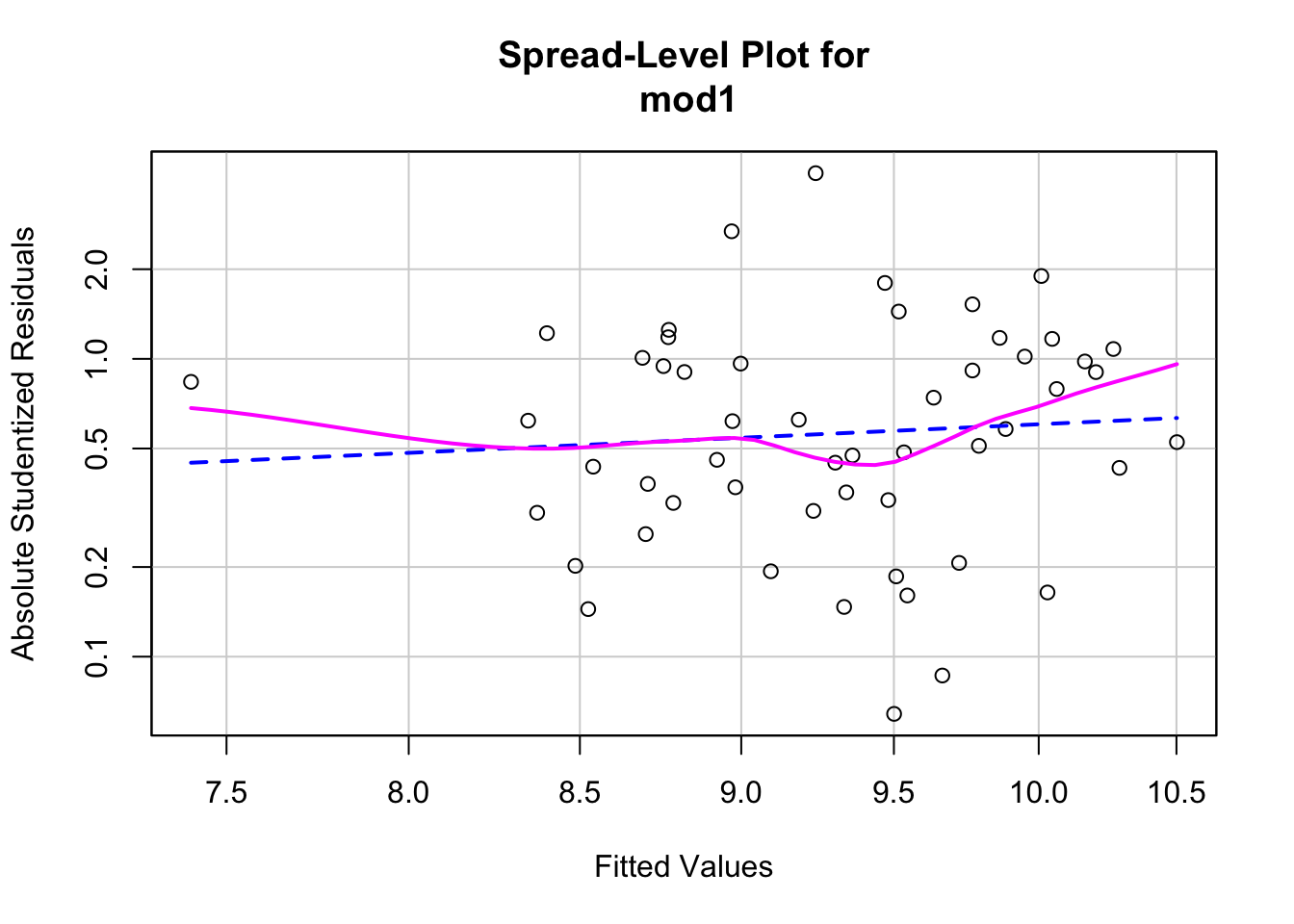

## 
## Suggested power transformation:  0.0094611

Step wise Regresión multiple

#formulación de un modelo nulo y un modelo completo
modNulo1 <- lm(death1K ~ 1, data = dsc)
modFull1 <- lm(death1K ~ doctor100K+hosp100K+income1K+density, 
              data = dsc)
#procedimiento stepwise
bmistep2 <- step(modNulo1,
                scope = list(lower=modNulo1, upper=modFull1,
                             direction="both"))

## Start:  AIC=54.87
## death1K ~ 1
## 
##              Df Sum of Sq    RSS    AIC
## + density     1   11.0765 132.65 52.624
## <none>                    143.73 54.875
## + income1K    1    4.2517 139.48 55.283
## + doctor100K  1    1.9262 141.80 56.159
## + hosp100K    1    1.7578 141.97 56.222
## 
## Step:  AIC=52.62
## death1K ~ density
## 
##              Df Sum of Sq    RSS    AIC
## <none>                    132.65 52.624
## + hosp100K    1    3.9272 128.72 53.031
## + income1K    1    2.7132 129.94 53.529
## + doctor100K  1    1.7471 130.91 53.921
## - density     1   11.0765 143.73 54.875

summary(bmistep2)

## 
## Call:
## lm(formula = death1K ~ density, data = dsc)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -5.7119 -1.0315  0.1011  1.0413  2.9696 
## 
## Coefficients:
##              Estimate Std. Error t value Pr(>|t|)    
## (Intercept) 10.387997   0.569350  18.245   <2e-16 ***
## density     -0.009782   0.004740  -2.064   0.0442 *  
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 1.613 on 51 degrees of freedom
## Multiple R-squared:  0.07707,    Adjusted R-squared:  0.05897 
## F-statistic: 4.259 on 1 and 51 DF,  p-value: 0.04416

“Activities reported in this website was supported by the National Institute of General Medical Sciences of the National Institutes of Health under Award Number R25GM121270. The content is solely the responsibility of the authors and does not necessarily represent the official views of the National Institutes of Health.”

Regresion_Multiple

Regresión Múltiple

Lista de paquetes a instalar

Lista de archivos a usar

Objetivos Generales

Regresión Lineal Múltiple

Ejemplo 1 y Datos

Pruebas de supuestos para regresión múltiples

Normalidad

Pruebas de Normalidad

Prueba de Autocorrelación

Prueba de linealidad del modelo

Prueba de multicolinealidad

Gráfica de regresiones en parejas, con línea de regresión

Prueba de Glauber para multicolinealidad

Modelos de regresión lineal múltiple

Modelo completo (todas las variables)

Modelo eliminando la variable Age, por ser la menos correlaciona con BMI, y tener la mayor correlación con Glucose

Modelo con interacción entre Age y Glucose

Selección automática de modelo - método “stepwise”

Comparación de modelos

Gráfica de coeficientes

Selección de modelo usando R-cuadrado ajustado y Mallow’s Cp para mejores modelos

EJERCICIO

Normalidad

Visualización

Pruebas

Prueb a de autocorelación de Durbin Watson

Multicolienarity

Visualizando colinearidad

El Modelo

Step wise Regresión multiple