Geom_area_densidad_freqpoly
Fecha de la ultima revisión
## [1] "2026-02-23"

Gráficos de área, densidad y histograma de linea con geom_dotplot, geom_density y geom-freqpoly
Librerías necesarias para producir los gráficos que siguen
library(ggversa) # paquete con los datos
library(tidyverse) # paquete que instala múltiples paquetes
library(gridExtra) # Un paquete para organizar las figuras de ggplot2
library(janitor)1. Gráfico de área con geom_area
Este gráfico muestra cómo se distribuyen los valores de la variable
continua distance al agruparlos en intervalos (bins), igual
que en un histograma, pero rellenando el área bajo la curva. A
diferencia de un histograma clásico, aquí los límites entre bins se
suavizan visualmente, creando una representación más fluida de la
frecuencia.
Eje X: distancia del individuo al árbol más cercano
Eje Y: frecuencia de observaciones por intervalo
Interpretación: Podemos ver dónde se concentra la mayor parte de las distancias. Un área más alta corresponde a intervalos donde se encuentran más observaciones.
Este tipo de gráfico es ideal cuando queremos visualizar la forma general de la distribución sin enfatizar las divisiones discretas de un histograma.
DW=dipodium
DW=clean_names(DW)
a=ggplot(DW, aes(distance))
a+geom_area(stat="bin", fill="aquamarine", color="black")+
labs(x="Distancia (m) al árbol más cercano", y="Frecuencia")+
theme(axis.title=element_text(size=10,face="bold"))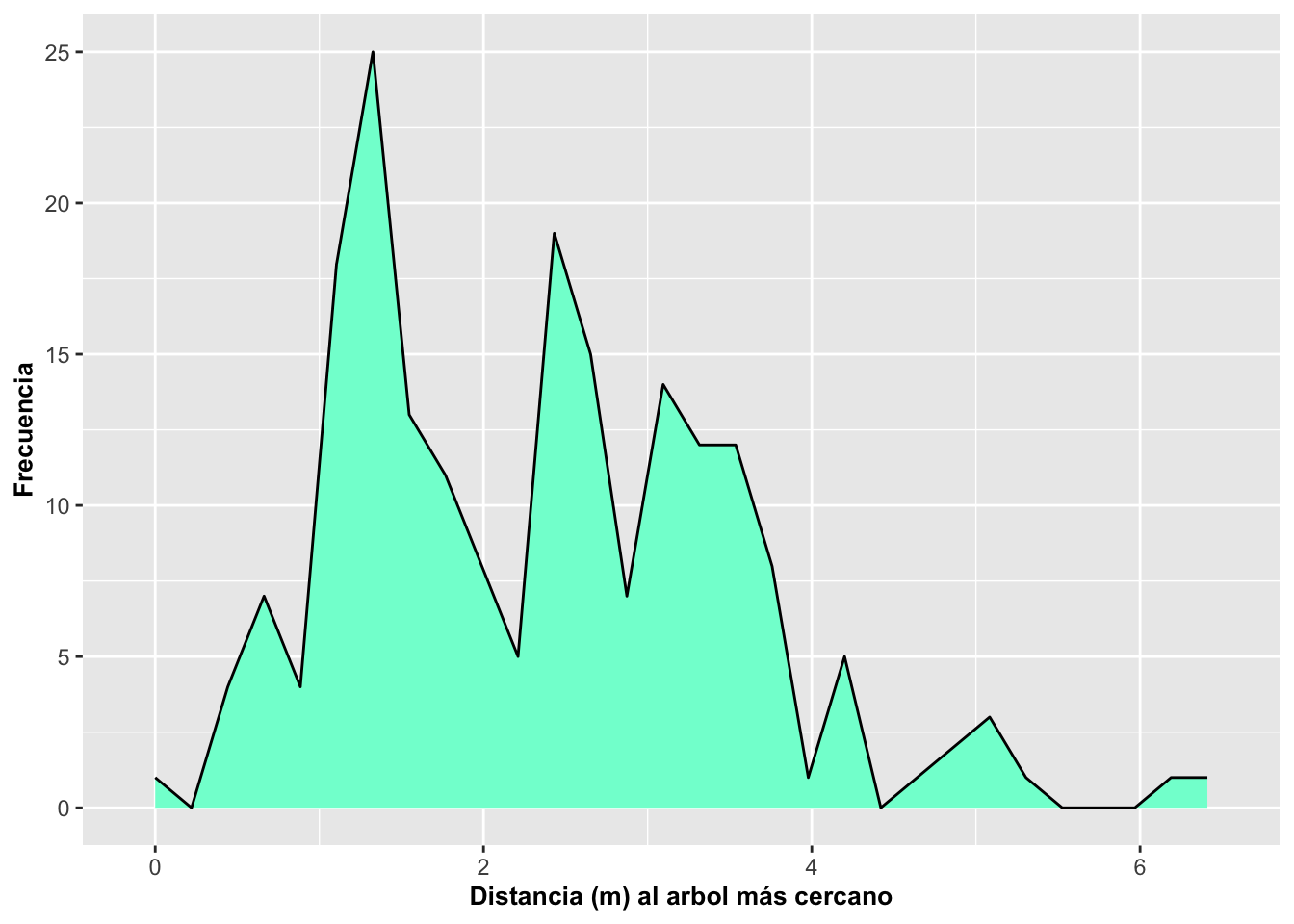
2. Gráfico de área con estilo de línea y transparencia
Aquí modificamos varios parámetros estéticos para mostrar cómo
geom_area() permite un alto nivel de personalización:
linetype = "twodash"cambia el estilo de la línea de contorno.color = "black"define el color del borde del área.size = 0.5controla el grosor de la línea.alpha = 0.1reduce la opacidad del color de relleno (haciéndolo casi transparente).
¿Qué nos permite esto?
Resaltar el contorno del área sin que el relleno opaque otros elementos del gráfico. Esto es útil cuando el área se superpone con otros elementos o cuando queremos destacar el patrón general pero sin saturar de color.
a=ggplot(DW, aes(distance))
a+geom_area(stat="bin", fill="steelblue1",
linetype="twodash", color="black", linewidth=0.5, alpha=0.1)+
labs(x="Distancia", y="Frecuencia")+
theme(axis.title=element_text(size=10,face="bold"))## `stat_bin()` using `bins = 30`. Pick better value `binwidth`.## Warning: Removed 1167 rows containing non-finite outside the scale range
## (`stat_bin()`).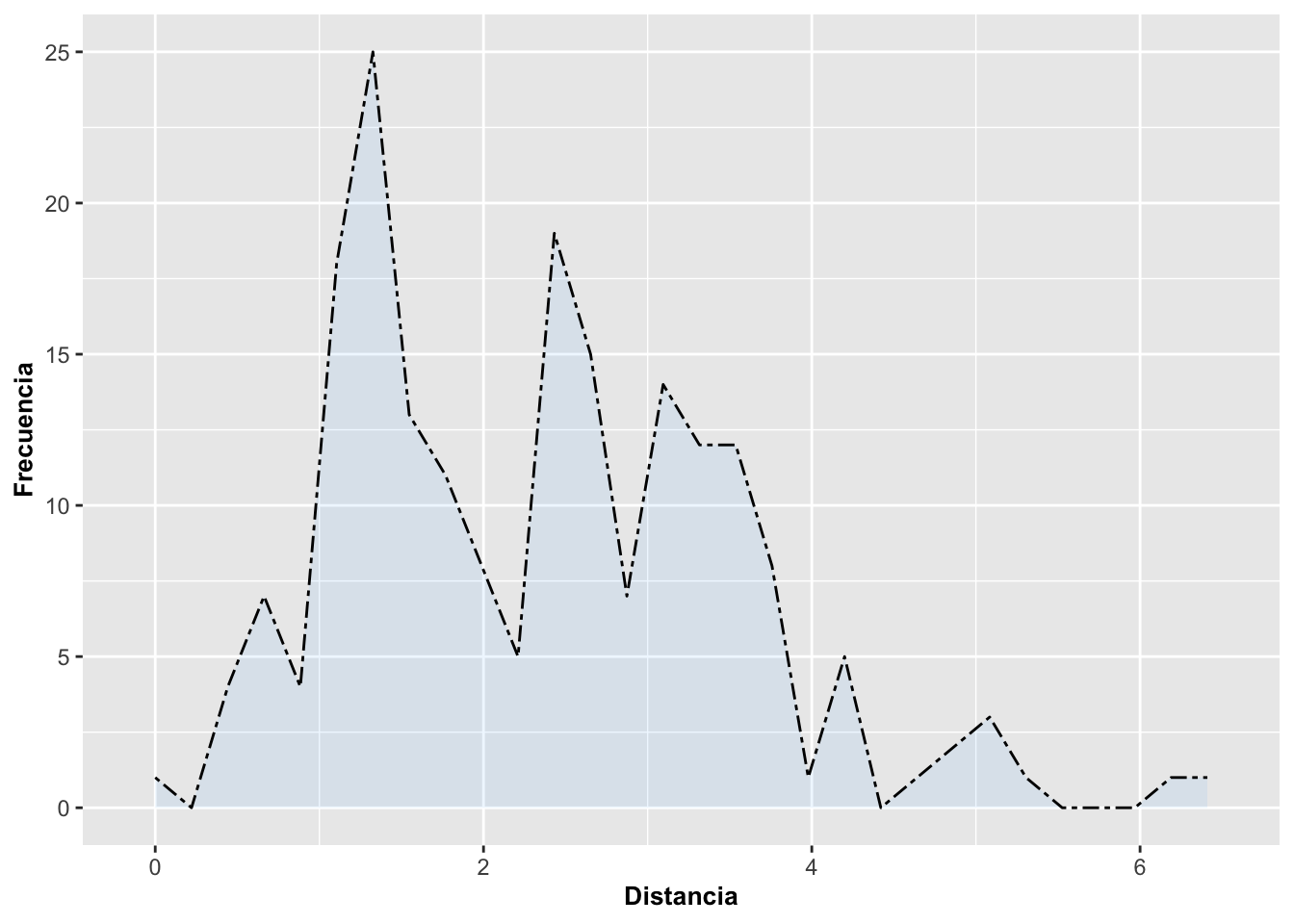
Los tipos de linetype
Vea las alternativas de “linetype” en este enlace linetype. Algunas de estas lineas se pueden llamar usando un nombre “blank”, “solid”, “dashed”, “dotted”, “dotdash”, “longdash”, “twodash”, o numeración “1F”, “F1”, “4C88C488”, “12345678.
par(mar=c(0,0,0,0))
# Set up the plotting area
plot(NA, xlim=c(0,1), ylim=c(10.5, -0.5),
xaxt="n", yaxt="n",
xlab=NA, ylab=NA )
# Draw the lines
for (i in 0:10) {
points(c(0.25,1), c(i,i), lty=i, lwd=2, type="l")
}
# Add labels
text(0, 0, "0. 'blank'" , adj=c(0,.5))
text(0, 1, "1. 'solid'" , adj=c(0,.5))
text(0, 2, "2. 'dashed'" , adj=c(0,.5))
text(0, 3, "3. 'dotted'" , adj=c(0,.5))
text(0, 4, "4. 'dotdash'" , adj=c(0,.5))
text(0, 5, "5. 'longdash'", adj=c(0,.5))
text(0, 6, "6. 'twodash'" , adj=c(0,.5))
text(0, 7, "6. '1F'" , adj=c(0,.5))
text(0, 8, "6. 'F1'" , adj=c(0,.5))
text(0, 9, "6. '4C88C488'" , adj=c(0,.5))
text(0, 10, "6. '12345678'" , adj=c(0,.5))
3. Gráfico con linetype avanzado
Este ejemplo muestra cómo usar un patrón de línea más complejo
mediante códigos hexadecimales de linetype como
"4C88C488".
Cambiar el estilo de línea puede servir para distinguir múltiples grupos en un gráfico o para mejorar la legibilidad en blanco y negro.
color = "orange"yalpha = 0.5producen un contraste fuerte tanto en el contorno como en la superficie.
Este gráfico demuestra que geom_area es altamente
personalizable incluso para presentaciones donde los estilos visuales
deben ser diferenciables sin usar color.
a=ggplot(DW, aes(distance))
a+geom_area(stat="bin", fill="steelblue1",
linetype="4C88C488", color="orange", linewidth=.4, alpha=0.5)+
labs(x="Distancia", y="Frecuencia")+
theme(axis.title=element_text(size=10,face="bold"))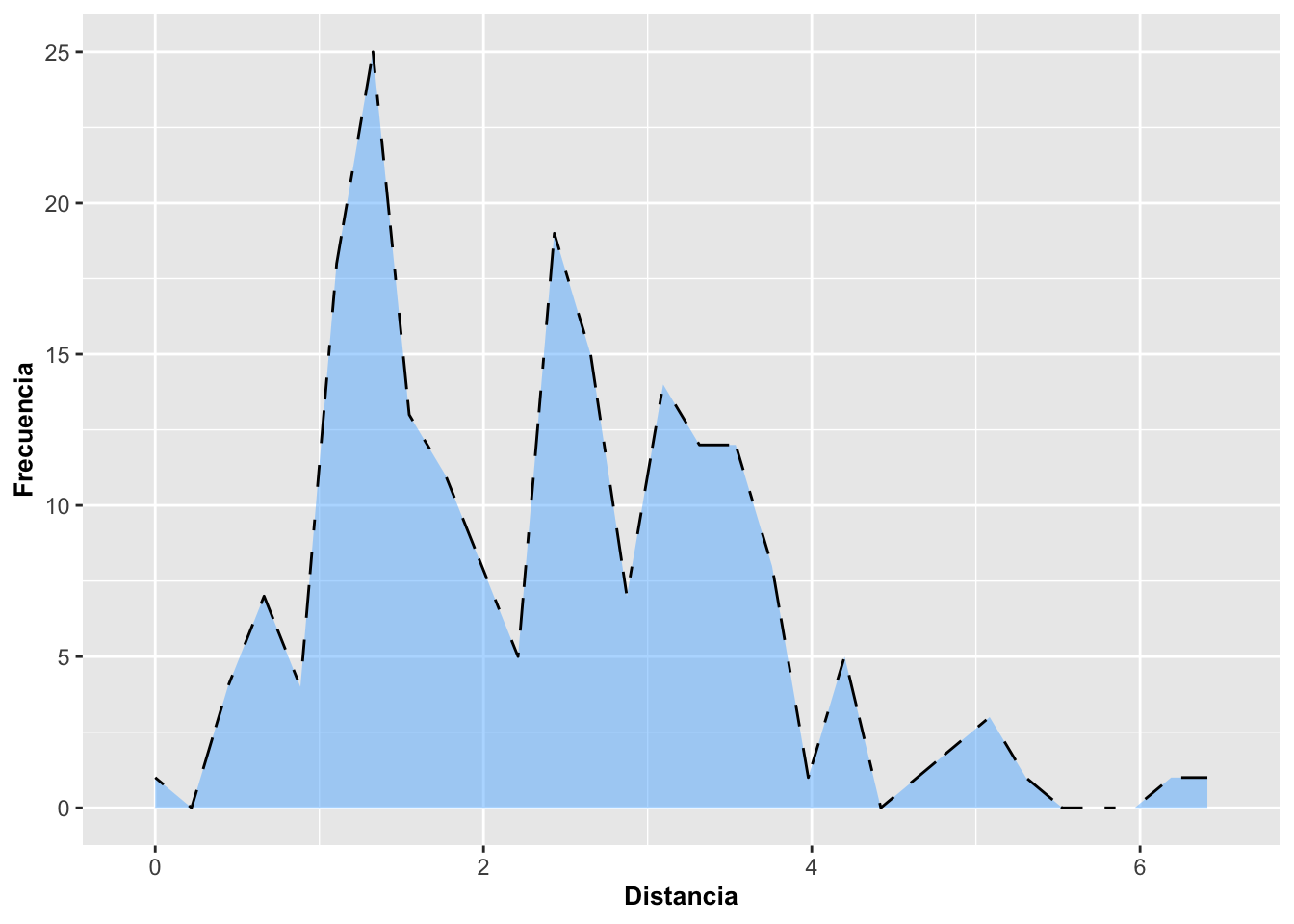
4. Gráfico de área con múltiples años (facetado)
Este gráfico presenta la distribución del número de camas hospitalarias por cada 1000 habitantes, separando (facetando) cada año en un panel diferente:
facet_wrap(~Year)crea un panel por cada año.fill = factor(Year)asigna un color distinto a cada año.bins = 30uniformiza la resolución del análisis.
Qué muestra este gráfico
Permite comparar rápidamente cómo cambia la distribución de camas entre años, por ejemplo:
si la media sube o baja
si la dispersión aumenta (indicando desigualdad entre países)
si aparecen nuevos picos o valores extremos
El uso de áreas superpuestas y facetado facilita visualizar tendencias temporales sin mezclar las distribuciones en un solo panel.
## Pais Year Poblacion Camas
## 129 Turkey 2006 68704721 2.7000
## 130 Turkmenistan 2006 4801594 4.3331
## 131 Ukraine 2006 46787750 8.7000
## 132 United States 2006 298379912 3.1000
## 133 Uruguay 2006 3331041 2.9000
## 134 Yemen, Rep. 2006 21093973 0.7000## [1] 1996 2006## [1] Armenia Australia Austria
## [4] Azerbaijan Bahamas, The Barbados
## [7] Belarus Belize Bolivia
## [10] Bulgaria Burkina Faso Canada
## [13] Chile China Colombia
## [16] Costa Rica Croatia Cuba
## [19] Egypt, Arab Rep. El Salvador Estonia
## [22] Finland France Georgia
## [25] Germany Greece Guyana
## [28] Hungary Iran, Islamic Rep. Ireland
## [31] Israel Italy Jamaica
## [34] Japan Kazakhstan Korea, Rep.
## [37] Kyrgyz Republic Latvia Lithuania
## [40] Macedonia, FYR Malaysia Malta
## [43] Mexico Moldova Nepal
## [46] Nicaragua Norway Paraguay
## [49] Poland Portugal Romania
## [52] Russian Federation Slovak Republic Slovenia
## [55] Spain St. Lucia Suriname
## [58] Syrian Arab Republic Tajikistan Trinidad and Tobago
## [61] Tunisia Turkey Turkmenistan
## [64] Ukraine United States Uruguay
## [67] Yemen, Rep.
## 67 Levels: Armenia Australia Austria Azerbaijan Bahamas, The ... Yemen, Rep.a=ggplot(Camas_Hospital, aes(Camas, fill=factor(Year)))
a+geom_area(stat="bin",bins=30, alpha=0.5)+
xlab("Número de camas por \n cada 1000 habitantes")+
ylab("Frecuencia")+
scale_y_continuous(breaks=c(0,2,4, 6:8))+ # Cambio en la escala de eje
scale_x_continuous(breaks=c(5:15))+
theme(axis.title=element_text(size=10,face="bold"))+
facet_wrap(~Year)+
theme(legend.position=c(0.5, 0.5))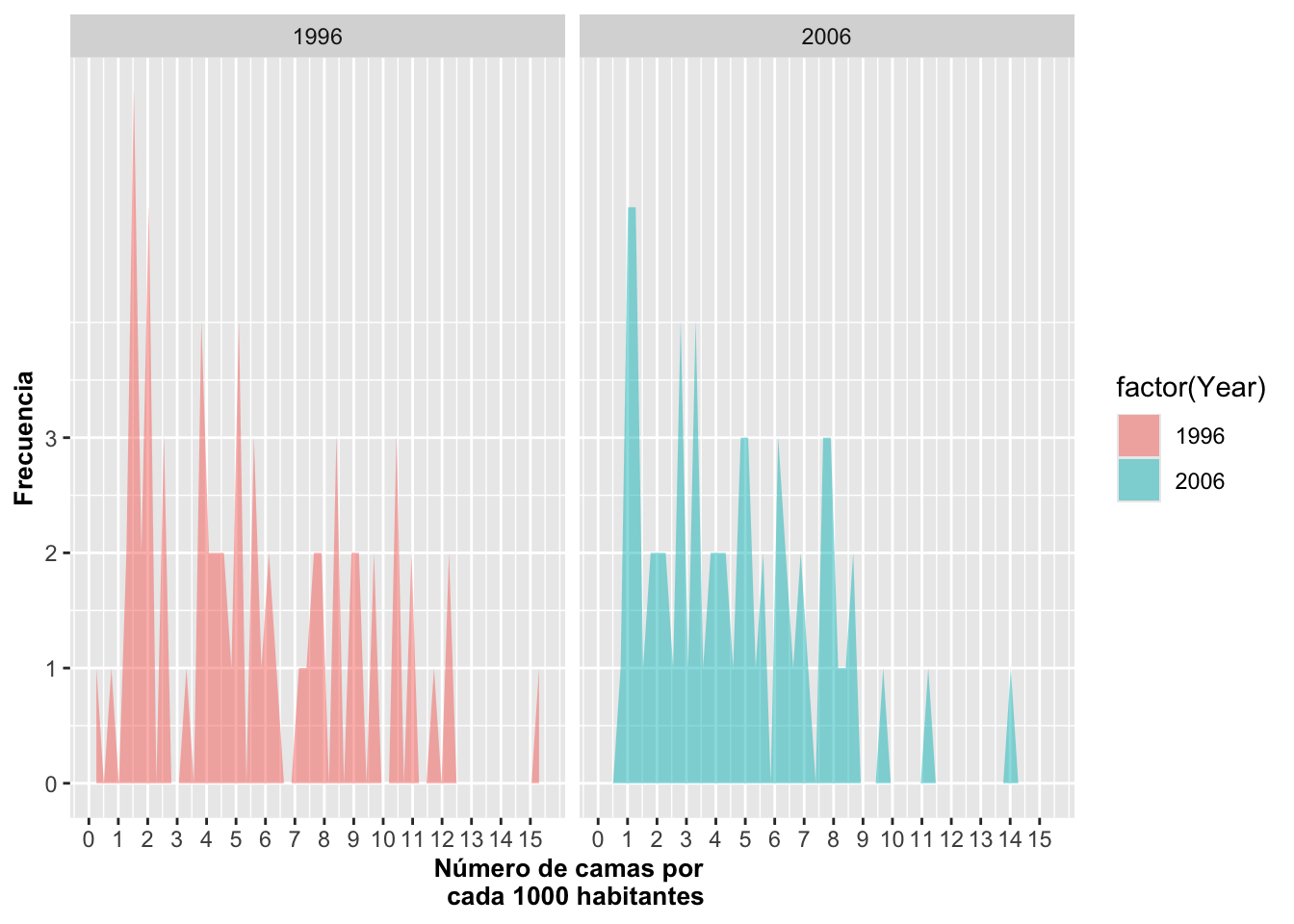
## # A tibble: 2 × 2
## # Groups: Year [2]
## Year n
## <int> <int>
## 1 1996 67
## 2 2006 675. La función densidad aes(after_stat(density))
Aquí se transforma el eje Y para mostrar densidad en lugar de frecuencia.
La fórmula
aes(y = ..density..)oaes(after_stat(density))normaliza el área bajo la curva a 1.Esto facilita comparar años incluso si el número de países en cada año no es el mismo.
Interpretación
En este gráfico, la forma muestra cómo se distribuye proporcionalmente el número de camas:
En 1996 la densidad tiene un pico claro alrededor de cierto valor.
En 2006 la distribución es más dispersa, lo que implica mayor heterogeneidad entre países.
Este cambio es mucho más evidente con una función de densidad que con frecuencias.
## Pais Year Poblacion Camas
## 1 Armenia 1996 3173425 7.13
## 2 Australia 1996 18311000 8.50
## 3 Austria 1996 7959017 9.30
## 4 Azerbaijan 1996 7763000 9.81
## 5 Bahamas, The 1996 283792 3.94
## 6 Barbados 1996 265940 7.56a = ggplot(Camas_Hospital, aes(Camas, fill = factor(Year)))
a + geom_area(aes(y = after_stat(density)), stat = "bin", alpha = 0.5)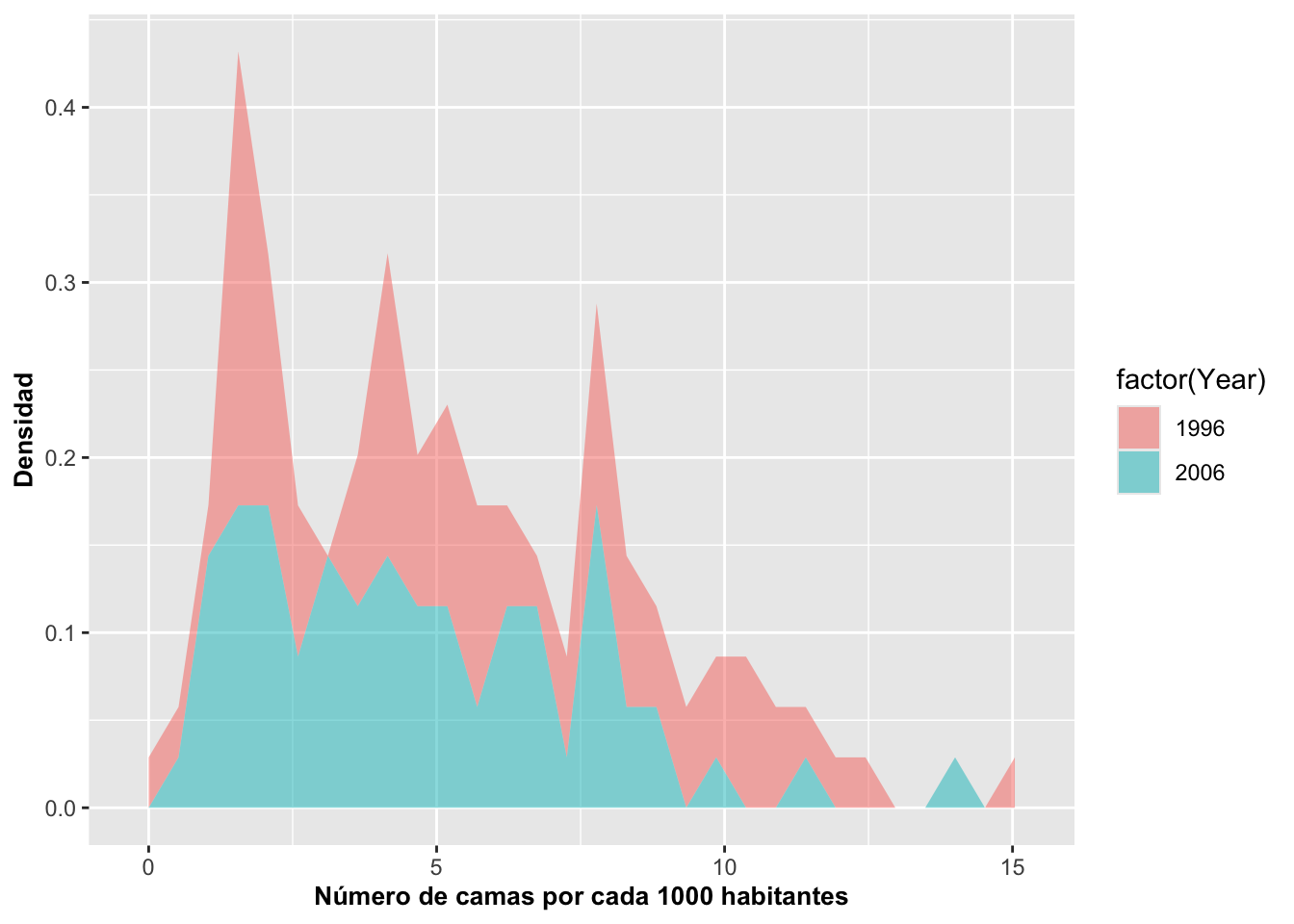
xlab("Número de camas por cada 1000 habitantes")+
ylab("Densidad")+
theme(axis.title=element_text(size=10,face="bold"))## NULLOpciones y Parametros de geom_area:
ggplot (el archivo de datos, aes(la variable continua)) +geom_area(stat= bin, x, y, alpha, color, fill, linetype, size)
- alpha: la intensidad del color
- color: el color de la línea alrededor del área
- fill: el color del área
- linetype: representa el estilo de línea
- size: representa el grosor de la línea
- stat: el método predeterminado es {identity}, que representa los datos, o la transformación estadística
Gráfico de densidad con geom_density
Un gráfico de densidad, también conocido como una función de probabilidad de densidad, pdf o probability density function en inglés, se utiliza con variables que contienen datos continuos. La función de densidad es continua en el rango de los valores, y la suma de todas la probabilidades es igual a uno. Vimos anteriormente que se puede visualizar la densidad también con geom_area y geom_histogram. La función geom_density facilita la producción del gráfico y amplía las alternativas como se explica en breve.
¿Qué es un kernel?
Estimar la densidad de los datos en un gráfico requiere seleccionar
un parámetro, un kernel, para suavizar la distribución.
El más utilizado es el gaussian, que representa la
distribución normal o conocida comúnmente como distribución de forma de
campana. Si no se especifica cuál kernel utilizar, la
distribución normal es la predeterminada; por ejemplo, cuando se
especifica geom_density() sin ninguna otra
opción.
Otra alternativa es usar geom_density(kernel =
c(kernel={gaussian}), u otras alternativas. Otros parámetros
para kernel son:
- rectangular,
- triangular,
- epanechnikov,
- biweight,
- cosine,
- optcosine,
- gaussian
EL kernel es un tipo especial de función de probabilidad de densidad que tiene ciertas propiedades específicas, ya sea que esta no sea negativa y con valores reales de manera tal que el gráfico salga simétrico, y que la suma de la integral sea igual a uno. Se añadió también geom_density para comparar el resultado de las dos funciones.
Note que en el gráfico siguiente se usó el parámetro alpha=0.4. Este modifica la transparencia del color azul del parámetro fill=blue. La intensidad de alpha=0.4 puede variar de 0 a 1, tal como se ha explicado anteriormente. En el ejemplo a continuación se utilizan los datos de la Dipodium rosea otra vez.
a=ggplot(DW, aes(distance))
a+
geom_area(aes(y=after_stat(density)),stat="bin", alpha=0.5)+
geom_density(kernel = c(kernel="gaussian"),
alpha=0.4, fill="blue")+
labs(x="Distancia", y="Densidad")+
theme(axis.title=element_text(size=10,face="bold"))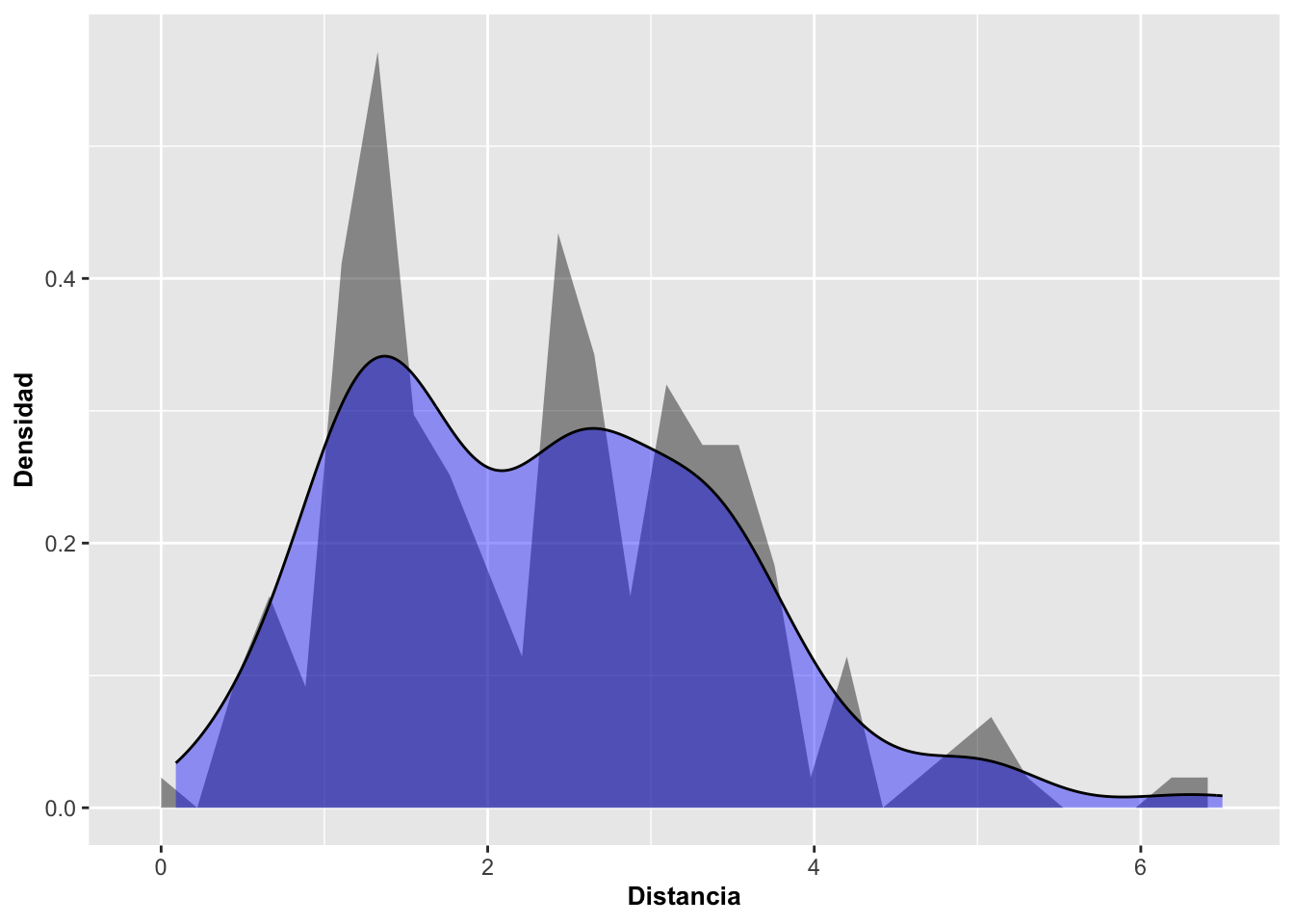
## [1] 12.345938 11.455697 9.098813 14.423036 5.264083 4.606147 10.946535
## [8] 5.956117 13.027305 11.434892 8.614728 10.027732 6.082915 8.904927
## [15] 7.643237 9.755155 15.031120 3.238201 9.273649 5.013799 15.595688
## [22] 6.530513 7.178937 7.580008 5.753668 12.734429 8.066263 8.157481
## [29] 14.034173 11.302105 15.961620 9.043862 6.240708 8.720294 3.280321
## [36] 3.748678 10.271360 9.788893 7.225322 3.695296 6.467206 9.665869
## [43] 10.607588 13.890898 10.522726 14.558985 9.745997 8.961832 13.887913
## [50] 11.561491 11.399371 5.693231 5.933830 13.334215 3.595941 12.424202
## [57] 7.260240 10.101442 10.999280 10.434961 5.326190 13.469702 5.380125
## [64] 13.533248 14.781080 17.906407 10.055000 3.054788 11.229521 10.501178
## [71] 15.363302 17.246351 9.383893 7.948878 7.380118 13.514939 1.091542
## [78] 7.891934 7.278017 11.659059 6.264854 12.015965 8.339059 12.224788
## [85] 11.531794 6.319531 12.415492 18.439747 7.546451 4.041074 12.771784
## [92] 5.895152 11.324434 13.315826 5.083591 5.340779 7.871652 7.276426
## [99] 10.618138 6.691774## [1] 9.474244## [1] 3.669461a=ggplot(x, aes(x))
a+geom_area(aes(y=after_stat(density)),stat="bin", alpha=0.5)+
geom_density(kernel = c(kernel="gaussian"),
alpha=0.4, fill="blue")+
labs(x="values", y="Densidad")+
theme(axis.title=element_text(size=10,face="bold"))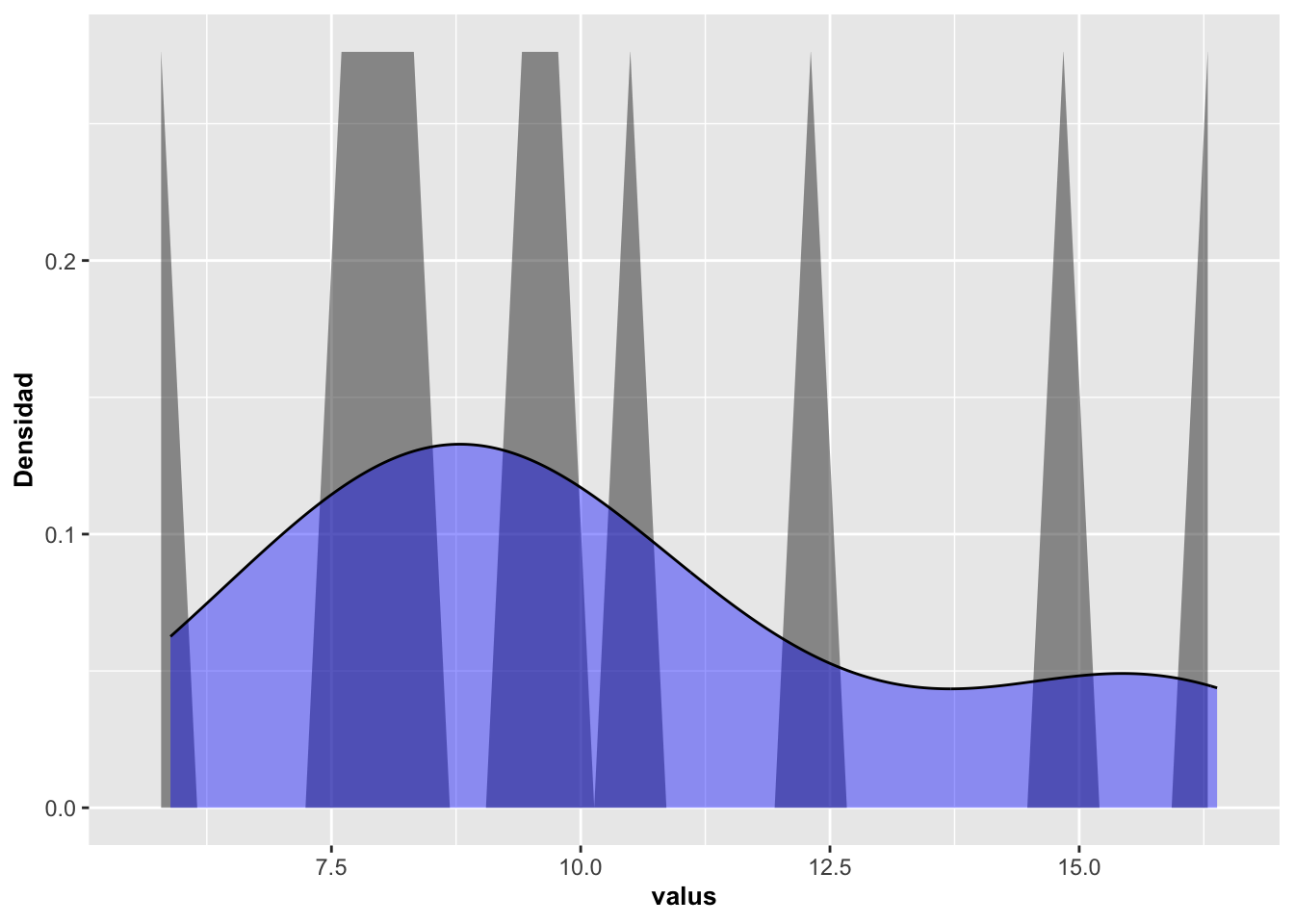
geom_density y datos simulados
La función de geom_density se puede entender mejor si se evalúa con datos simulados. Vamos a continuación a simular datos con diferentes tamaños de muestra para visualizar las densidades. En la simulación a continuación se crean 4 data frame con 2000, 500, 50 y 10 datos respectivamente con la función rnorm. Naturalmente, lo que se observa es que si los datos provienen de una distribución normal, entre más datos se incluyan, la distribución correspondiente se acerca más a como debe lucir una distribución normal. Pero, lo contrario es que con pocos datos, es probable que la densidad no se asemeje a la distribución teórica (normal).
a=rnorm(20000, 0, 1)
a=as.data.frame(a)
a=ggplot(a, aes(a))+
geom_density(kernel = c(kernel="gaussian"),
alpha=0.4, fill="yellow")+
labs(y="Densidad")+
theme(axis.title=element_text(size=10,face="bold"))
b=rnorm(500, 0, 1)
b=as.data.frame(b)
b=ggplot(b, aes(b))+
geom_density(kernel = c(kernel="gaussian"),
alpha=0.4, fill="red")+
labs(y="Densidad")+
theme(axis.title=element_text(size=10,face="bold"))
c=rnorm(50, 0, 1)
c=as.data.frame(c)
c=ggplot(c, aes(c))+
geom_density(kernel = c(kernel="gaussian"),
alpha=0.4, fill="blue")+
labs(y="Densidad")+
theme(axis.title=element_text(size=10,face="bold"))
d=rnorm(10, 0, 1)
d=as.data.frame(d)
d=ggplot(d, aes(d))+
geom_density(kernel = c(kernel="gaussian"),
alpha=0.4, fill="grey")+
labs(y="Densidad")+
theme(axis.title=element_text(size=10,face="bold"))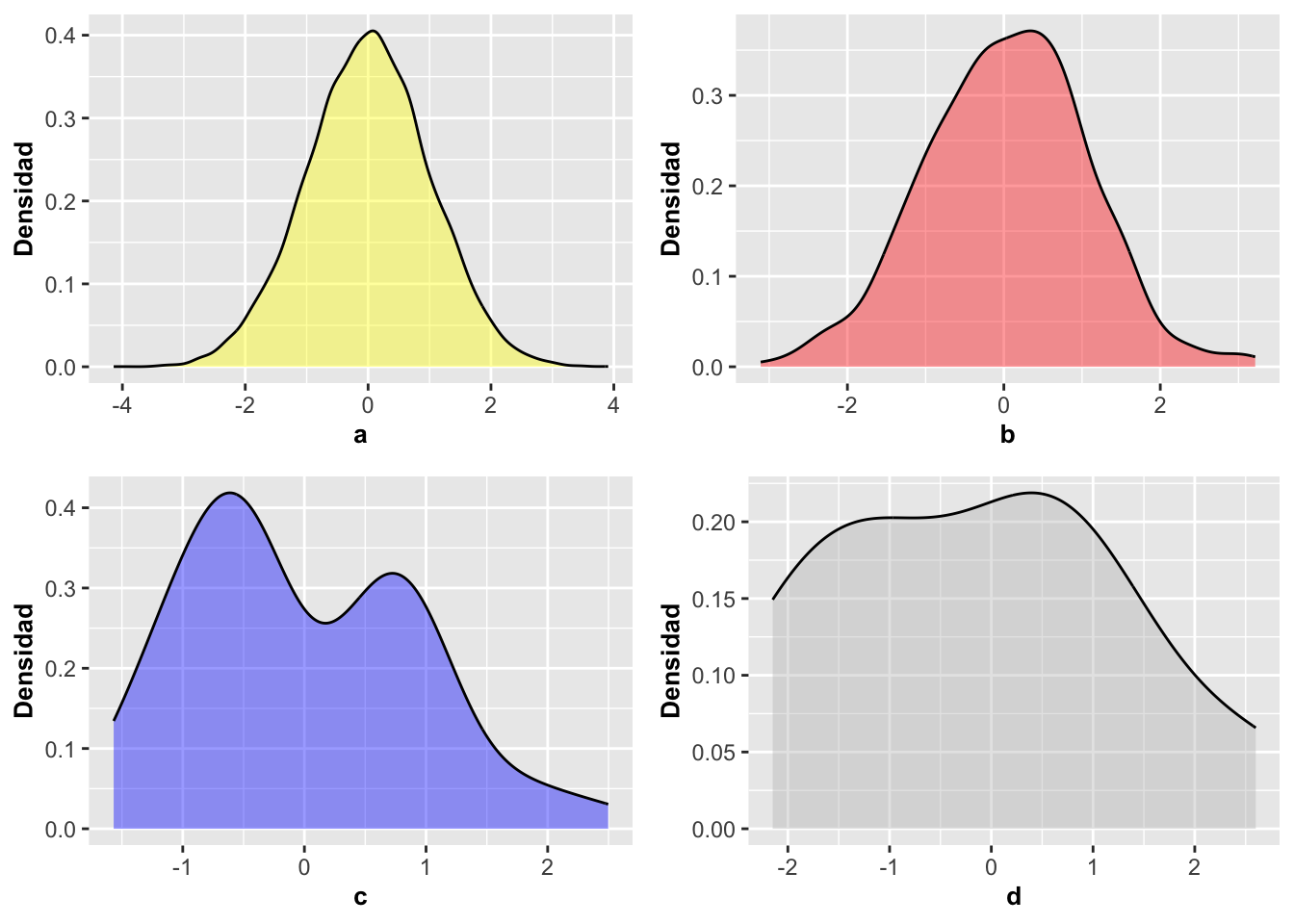
Excercise
According to data from Our World in Data, the mean world human height is approximately 170.8 cm for men and 164.7 cm for women, with a standard deviation of around 7 cm for both genders. ## Key points:
- Male mean: 170.8 cm
- Female mean: 164.7 cm
- Standard deviation (both genders): around 7 cm
DO a figure of the density distribution of male and female human height and compare with the mean and standard deviation of world data
male_students=c(170.6, 180, 167.64, 185.93, 177,
177, 183, 185.4, 164.59, 187.96,
203,167.64,177.8, 180.7) # height in cm
male_students=as.data.frame(male_students)
male_students## male_students
## 1 170.60
## 2 180.00
## 3 167.64
## 4 185.93
## 5 177.00
## 6 177.00
## 7 183.00
## 8 185.40
## 9 164.59
## 10 187.96
## 11 203.00
## 12 167.64
## 13 177.80
## 14 180.70female_students=c(165.1, 164.6 , 162.6, 165.1,167.64,
161.5, 160.3, 167.64, 121.92, 164.59,
152.4, 152.4, 163, 157) # height in cm
female_students=as.data.frame(female_students)
female_students## female_students
## 1 165.10
## 2 164.60
## 3 162.60
## 4 165.10
## 5 167.64
## 6 161.50
## 7 160.30
## 8 167.64
## 9 121.92
## 10 164.59
## 11 152.40
## 12 152.40
## 13 163.00
## 14 157.00ggplot(male_students, aes(male_students))+
geom_density(kernel = c(kernel="gaussian"),
alpha=0.4, fill="grey")+
labs(y="Densidad")+
theme(axis.title=element_text(size=10,face="bold"))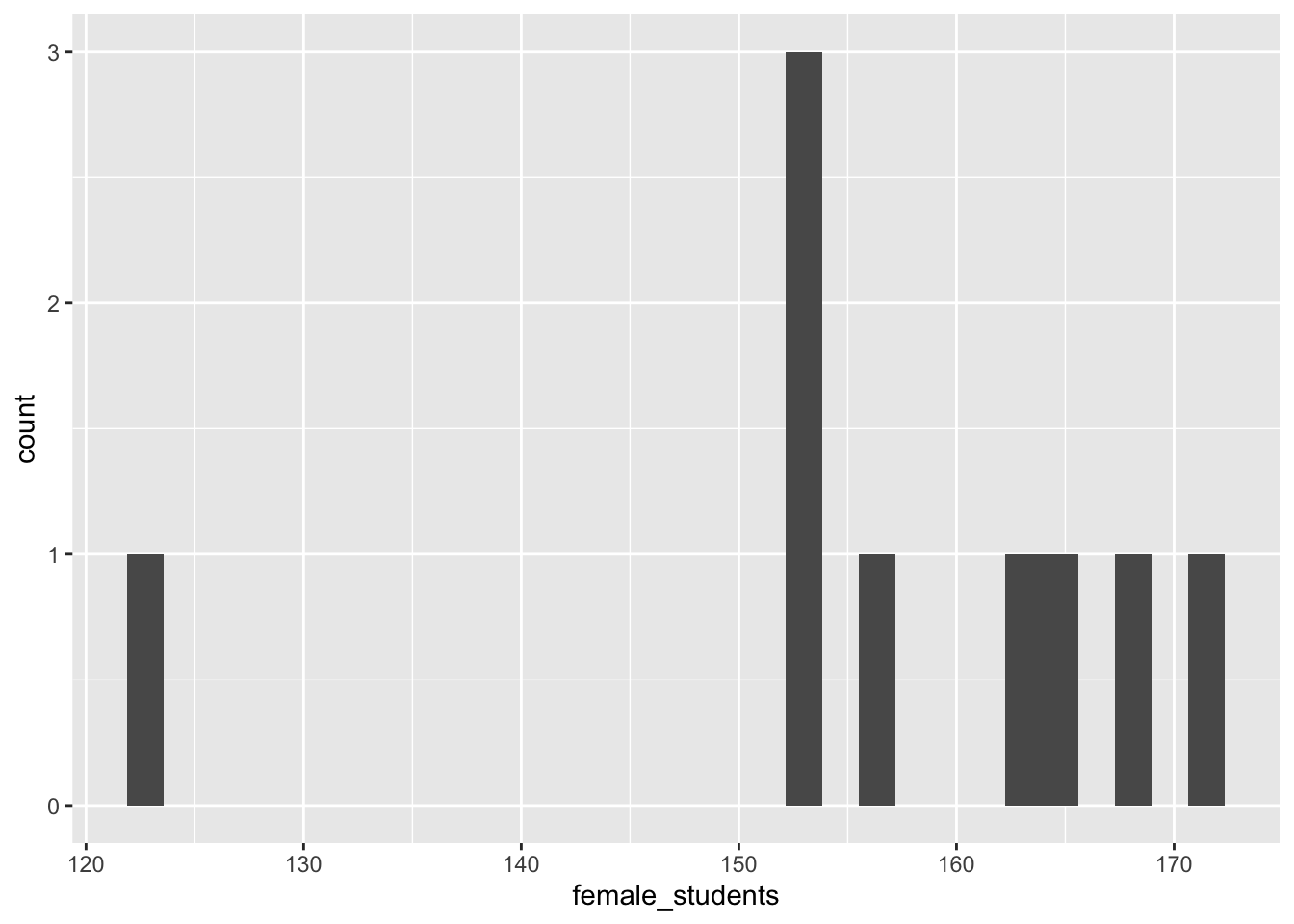
JOin the two data frames above to produce a single data frame with the height of all students, and then produce a density graph with the height of all students.
## altura.male_students altura.female_students
## 1 170.60 165.10
## 2 180.00 164.60
## 3 167.64 162.60
## 4 185.93 165.10
## 5 177.00 167.64
## 6 177.00 161.50
## 7 183.00 160.30
## 8 185.40 167.64
## 9 164.59 121.92
## 10 187.96 164.59
## 11 203.00 152.40
## 12 167.64 152.40
## 13 177.80 163.00
## 14 180.70 157.00Rename the colums to male and female
library(tidyverse)
height=height %>%
rename(male= altura.male_students,
female = altura.female_students)
height## male female
## 1 170.60 165.10
## 2 180.00 164.60
## 3 167.64 162.60
## 4 185.93 165.10
## 5 177.00 167.64
## 6 177.00 161.50
## 7 183.00 160.30
## 8 185.40 167.64
## 9 164.59 121.92
## 10 187.96 164.59
## 11 203.00 152.40
## 12 167.64 152.40
## 13 177.80 163.00
## 14 180.70 157.00Now let’s produce a density graph with the height of male and female in the same figure
ggplot(height)+
geom_density(aes(male), kernel = c(kernel="gaussian"),
alpha=0.4, fill="blue")+
geom_density(aes(female, kernel = c(kernel="gaussian"),
alpha=0.4, fill="pink"))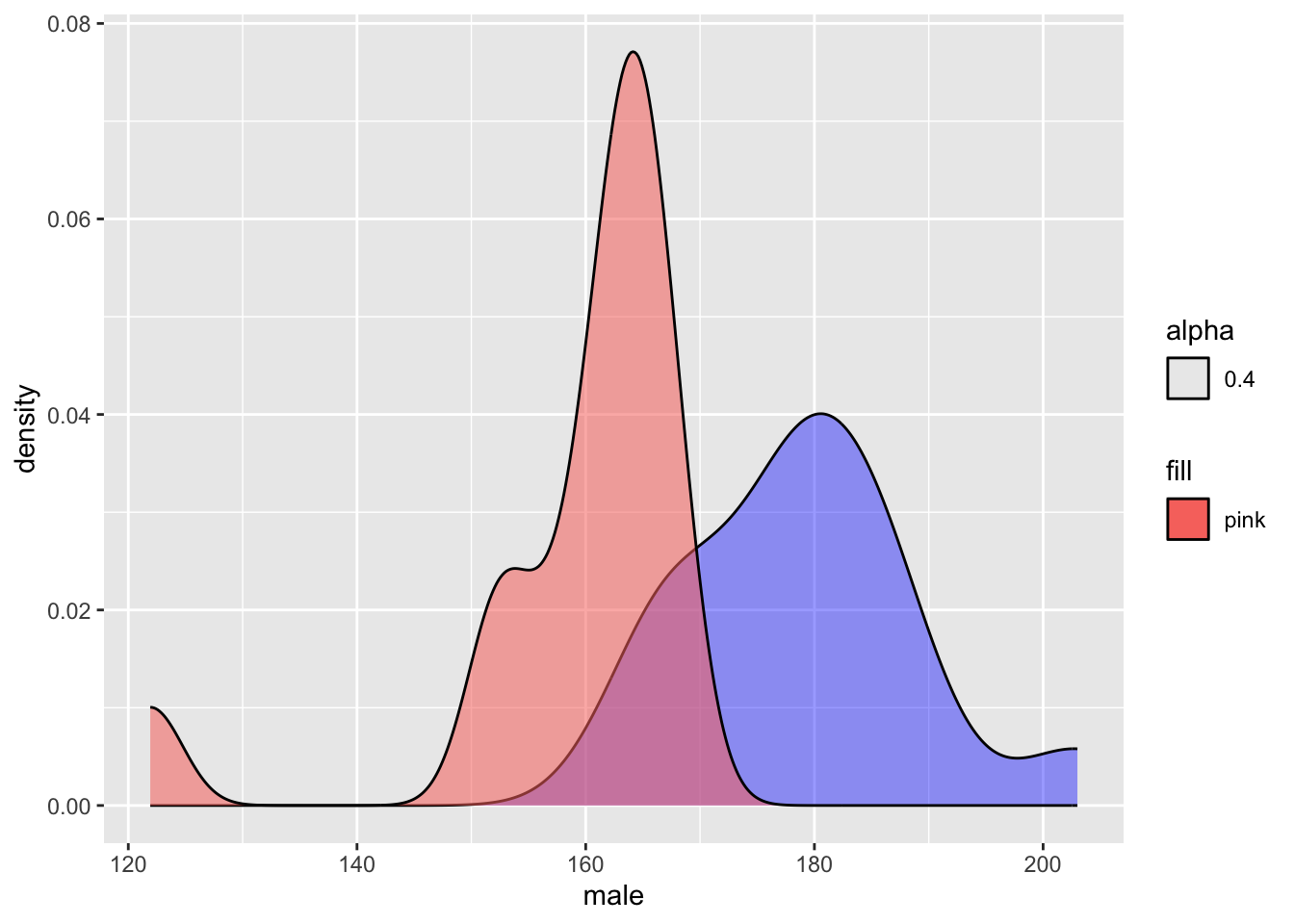
#set.seed(123987)
# Simulate
world_male=rnorm(10^4, 170.8, 7)
world_male=as.data.frame(world_male)
head(world_male)## world_male
## 1 174.1456
## 2 169.8483
## 3 167.5674
## 4 183.5702
## 5 167.7363
## 6 172.1285## [1] 179.6055 168.7823 174.6494 155.8378 171.3506 158.3817OVERLAY two figures from different data sets
male=ggplot()+
geom_density(aes(world_male), kernel = c(kernel="gaussian"),
alpha=0.4, fill="yellow", data=world_male)+
geom_histogram(aes(male_students, y=..density..), position="identity", data=male_students)
male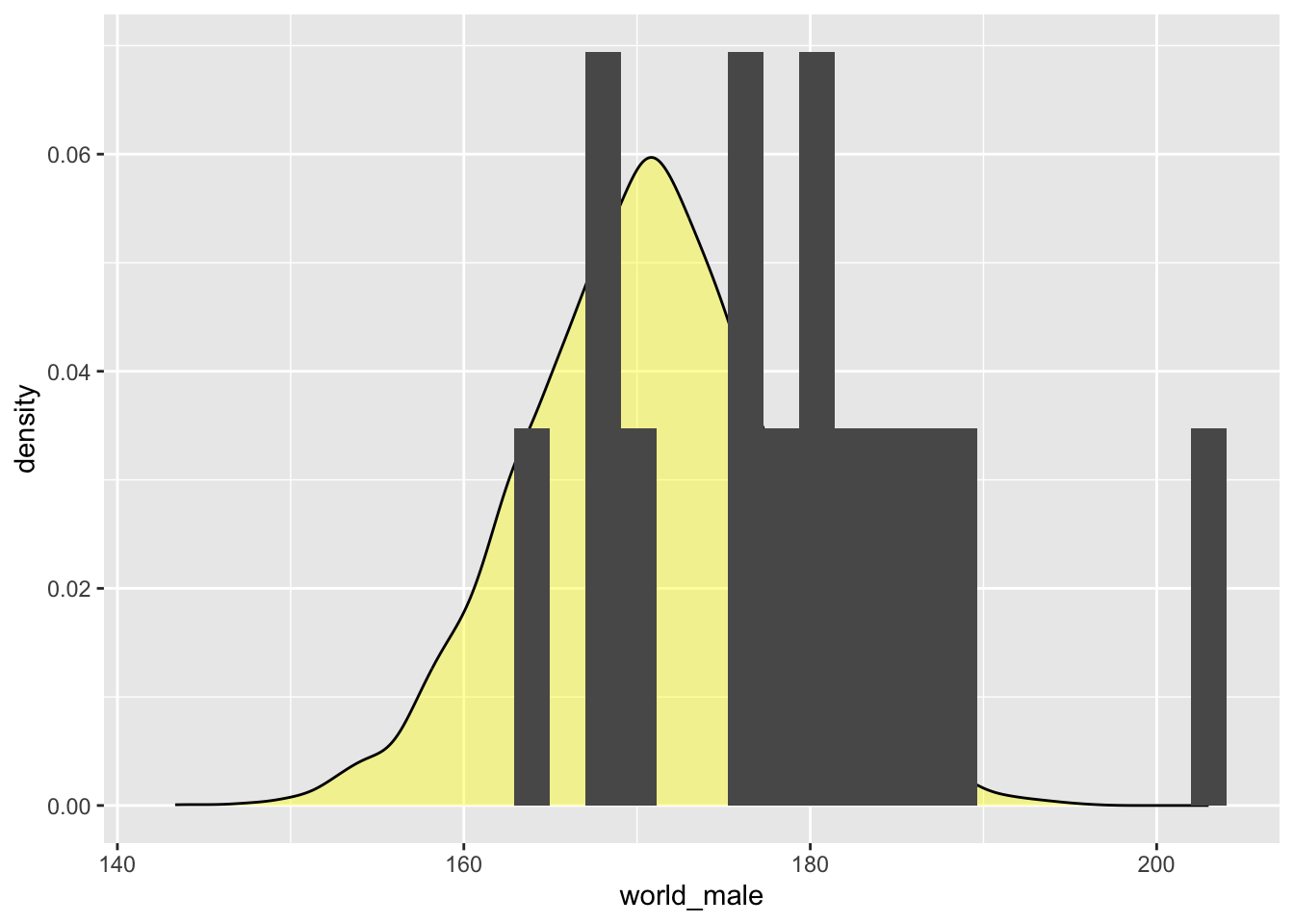
## NEW script, see after_stat(density)
male_2=ggplot()+
geom_density(aes(world_male), kernel = c(kernel="gaussian"),
alpha=0.4, fill="red", data=world_male)+
geom_histogram(aes(male_students, after_stat(density)), position="identity", data=male_students)
male_2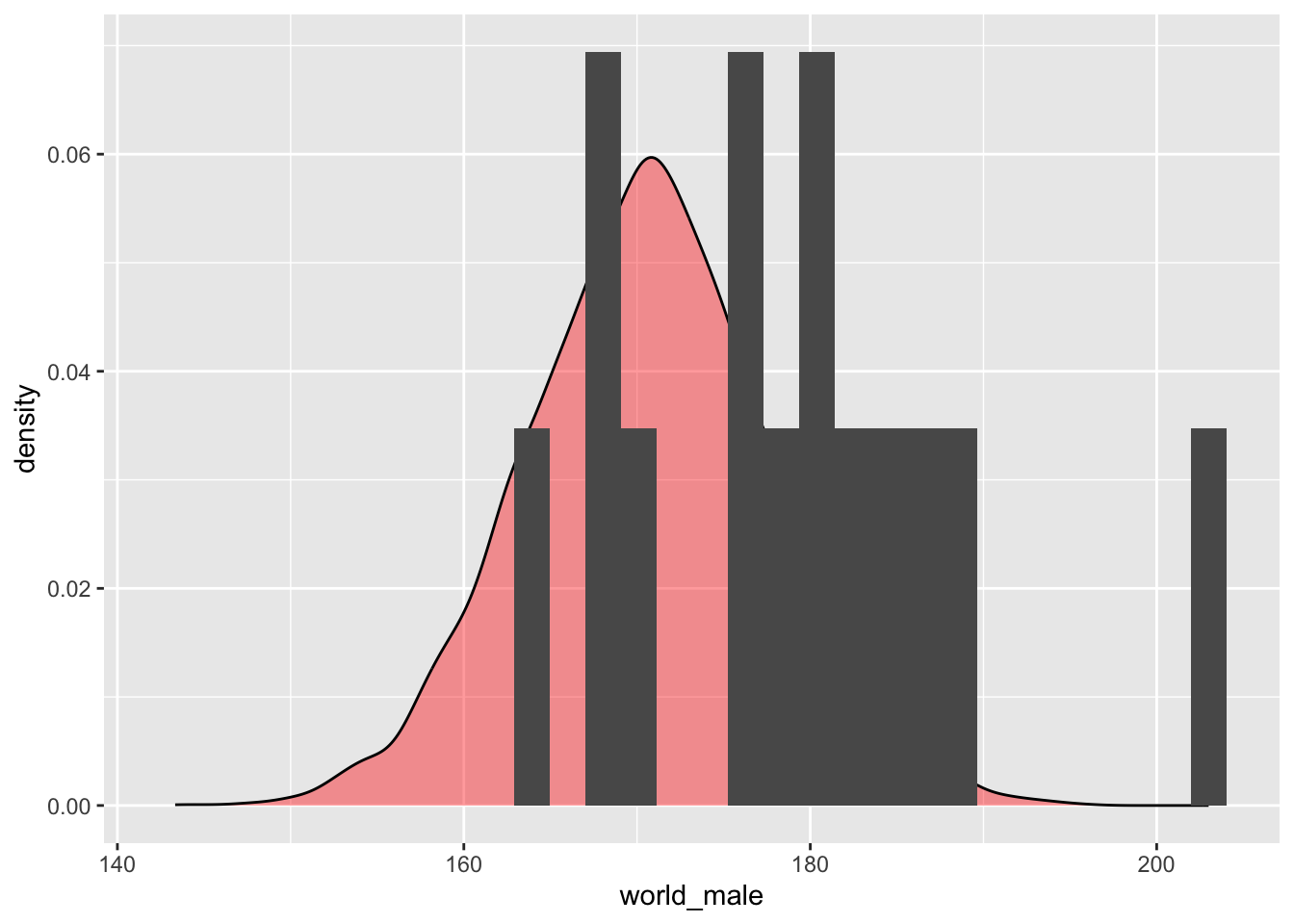
Opciones y Parametros de geom_density:
ggplot(el archivo de datos, aes(la variable continua))
- geom_density(kernel= {…}), x, y, alpha, color, fill, linetype, size,
weight
- … representa el parámetro deseado; ej. gaussian, triangular, rectangular, etc.
- alpha: la intensidad del color
- fill: el color del área
- color: el color de la línea alrededor del área
- linetype: representa el estilo de línea
- size: representa el grosor de la línea
- weight: para modificar el valor original; entonces no sería, por ejemplo, el conteo o suma de los valores si no un valor ponderado (promedio ponderado)
- geom_density(kernel= {…}), x, y, alpha, color, fill, linetype, size,
weight
Gráfico de frecuencia de polígono con geom_freqpoly
El gráfico de frecuencia de polígono es similar al gráfico de área y de densidad, la diferencia es que no se rellena el área con color. También se puede cambiar la cantidad de compartimentos usando binwidth. En el gráfico de polígono, es solamente la línea la que gráficamos y no hay parámetro de fill del área debajo de la línea.
a=ggplot(DW, aes(distance))
a+geom_freqpoly(binwidth=.1, color="#e3cc36")+ # Nota como seleccionar el color con "color picker" en el web.
labs(x="Distancia (m)", y="Frecuencia")+ # labels = labs
theme(axis.title=element_text(size=14,face="italic"))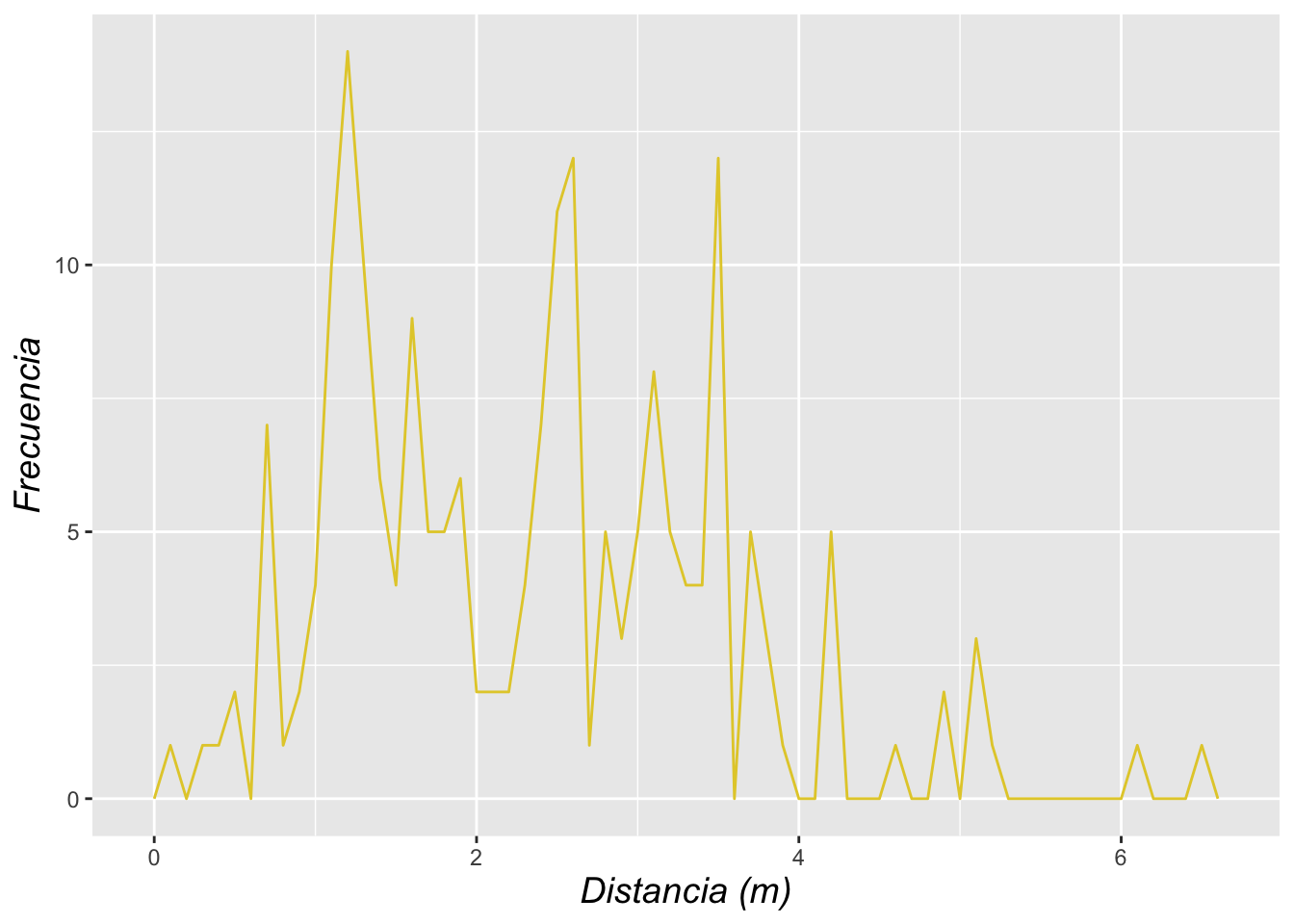
Se modifica otras opciones como sigue: intensidad del color con alpha, el tipo de línea con linetype y el grosor de la línea con size tal como se muestra a continuación.
DW%>%
drop_na()%>%
ggplot(aes(distance, colour=species_name))+
geom_freqpoly(alpha=1.0, size=1.0, binwidth=.1, linetype="longdash")+
labs(x="Distancia", y="Frecuencia")+
theme(axis.title=element_text(size=14,face="bold"))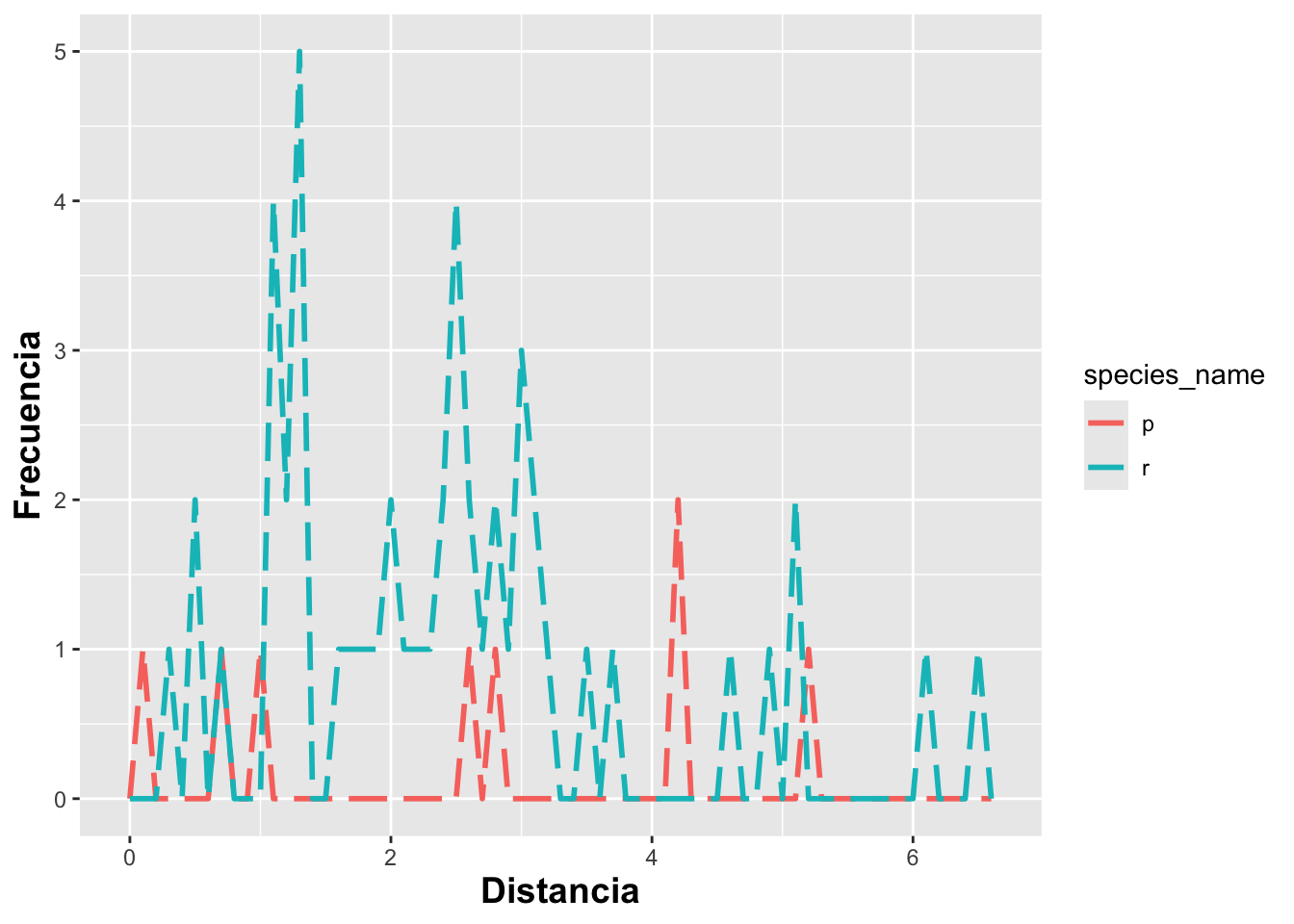
## # A tibble: 1,365 × 21
## tree_number tree_species dbh plant_number ramet_number distance orientation
## <int> <chr> <dbl> <int> <int> <dbl> <dbl>
## 1 1 E.o 75 1 1 2.47 40
## 2 1 E.o 76 2 1 1.97 50
## 3 2 E.o 76 3 1 1.95 350
## 4 3 E.o 58 4 1 3.24 210
## 5 4 E.o NA 5 1 0.85 80
## 6 5 E.o 59 6 1 2.62 160
## 7 5 E.o 59 7 1 2.82 170
## 8 6 E.o 8 8 1 3.12 245
## 9 7 E.o 11.5 9 1 1.12 208
## 10 8 E.o 8.5 10 1 0.75 360
## # ℹ 1,355 more rows
## # ℹ 14 more variables: number_of_flowers <dbl>, height_inflo <dbl>,
## # herbivory <chr>, row_position_nf <int>, number_flowers_position <int>,
## # number_of_fruits <int>, perc_fr_set <dbl>, pardalinum_or_roseum <chr>,
## # fruit_position_effect <int>, frutos_si_o_no <int>,
## # p_or_r_infl_lenght <chr>, num_of_fruits <int>, species_name <chr>,
## # cardinal_orientation <int>Opciones y Parametros de geom_freqpoly
ggplot(el archivo de datos, aes(la variable continua))
- geom_freqpoly(stat={bin}, x, y, alpha, color, linetype, size)
- alpha: la intensidad del color
- color: el color de la línea alrededor del área
- linetype: representa el estilo de línea; vea sección
- size: representa el grosor de la línea
- Actividad Usar el data set “dipodium” en el paquete “ggversa”.
Presenta un gráfico de la frecuencia de flores por
planta con geom_freqpoly.
- Cambia el color de la linea
- Cambiar la información de los ejes para texto más relevante
- Cambiar la intensidad de color de la linea
- Cambiar el tipo de linea