Gráficos de caja
Fecha de la ultima revisión
## [1] "2026-02-23"

Diagrama de caja con geom_boxplot
Para datos que no tienen una distribución normal, típicamente se usa un diagrama de caja para visualizar la distribución de los datos. El diagrama de caja distribuye los datos basándose en el rango del orden de tamaño o valor numérico. Primeramente, los datos son ordenados de menor a mayor. Los valores en el gráfico correspondiente representan los cuartiles 25, 50 y 75. Los bigotes (las líneas que se extienden de las cajas) representan 1.5 veces multiplicado por el rango intercuartil (RIC), o la distancia entre el primer cuartil (25) y el tercer cuartil (75). Los datos que están fuera de ese rango se representan con puntos. Los gráficos que usan muescas, o notch, las calculan de acuerdo a la siguiente fórmula: (1.58 x RIC) / (raíz cuadrada de la muestra). Utilizaremos nuevamente los datos de la orquídea Dipodium en los siguientes ejemplos, particularmente representando la cantidad de flores y el número de frutos.
En el primer gráfico a continuación, Fig. 1 (arriba a la izquierda), se muestra un diagrama de caja básico. Note que la variable en la primera x tiene valor de 1, lo que significa que hay un solo grupo. En el segundo gráfico, Fig. 2 (arriba a la derecha), se modifica con la opción de notch. En el tercer gráfico, Figura Fig. 3 (abajo a la izquierda), se cambió el color de la caja, la forma o shape de los valores atípicos o outliers, y su tamaño. En los tres primeros gráficos, se usan todos los datos en un mismo diagrama de caja. En el cuarto gráfico, Fig. 4 (abajo a la derecha), observamos la distribución de la cantidad de flores por el número de frutos observado por planta. Note que para este último caso en particular, hay más de un grupo.
Las muescas (notch)
Las muescas a los lados de un diagrama de caja se pueden interpretar como un intervalo de comparación alrededor de los valores de la mediana. La altura de la muesca es la mediana \(+/- 1,57 x IQR/sqrt(n)\) donde IQR es el rango intercuartíl definido por los percentiles 25 y 75 y n es el número de puntos de datos
Teoretical boxplot
## # A tibble: 47 × 1
## value
## <dbl>
## 1 1
## 2 8
## 3 9
## 4 10
## 5 100
## 6 101
## 7 102
## 8 103
## 9 104
## 10 105
## # ℹ 37 more rows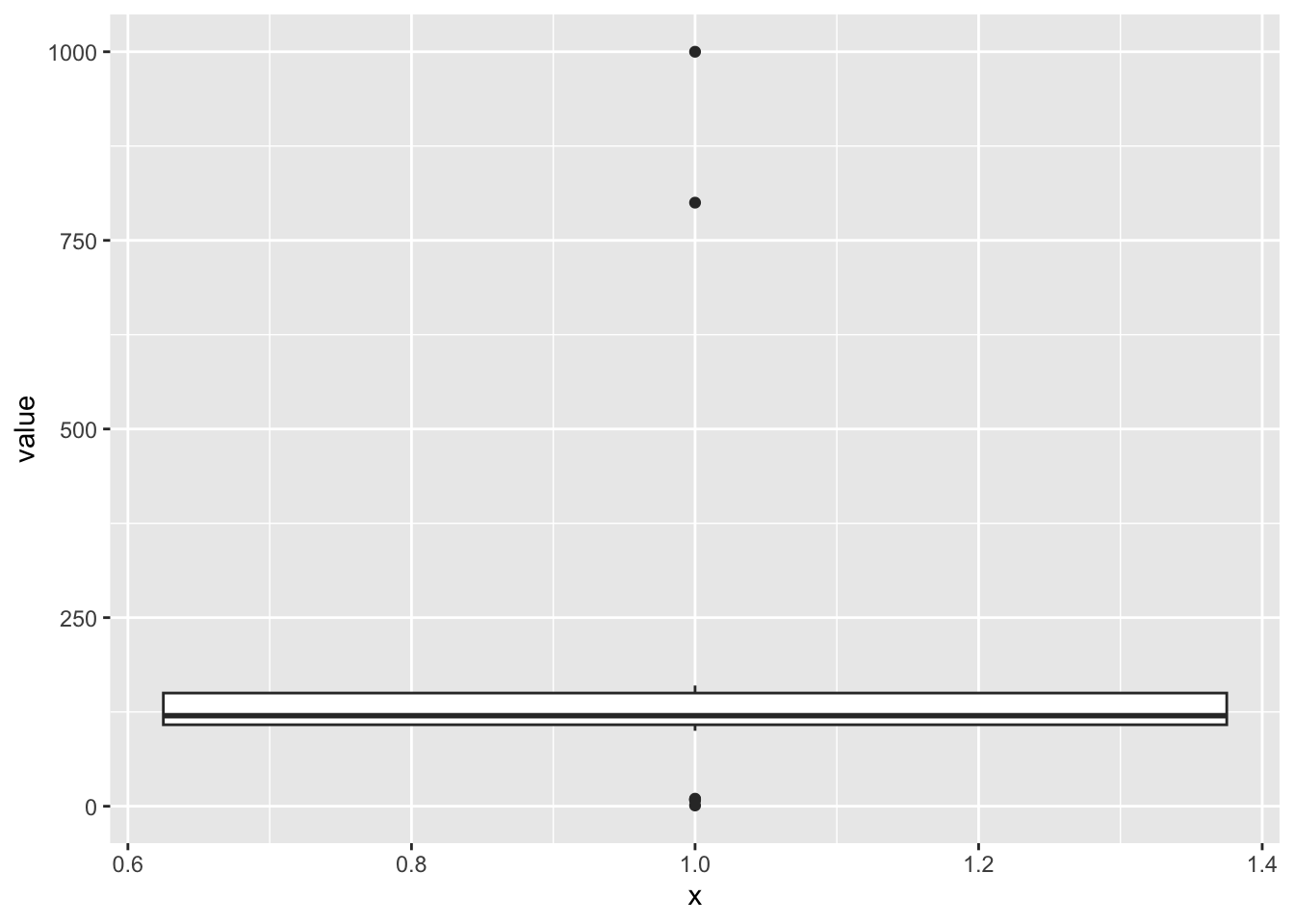
df2=as_tibble(c(2,3,2,2,4,11,8,2,5,5,3,4,2,3,3,3,4,9,2))
df2 %>%
ggplot(aes(value, x=1))+ # x=1 representa que hay solamente un grupo
geom_boxplot()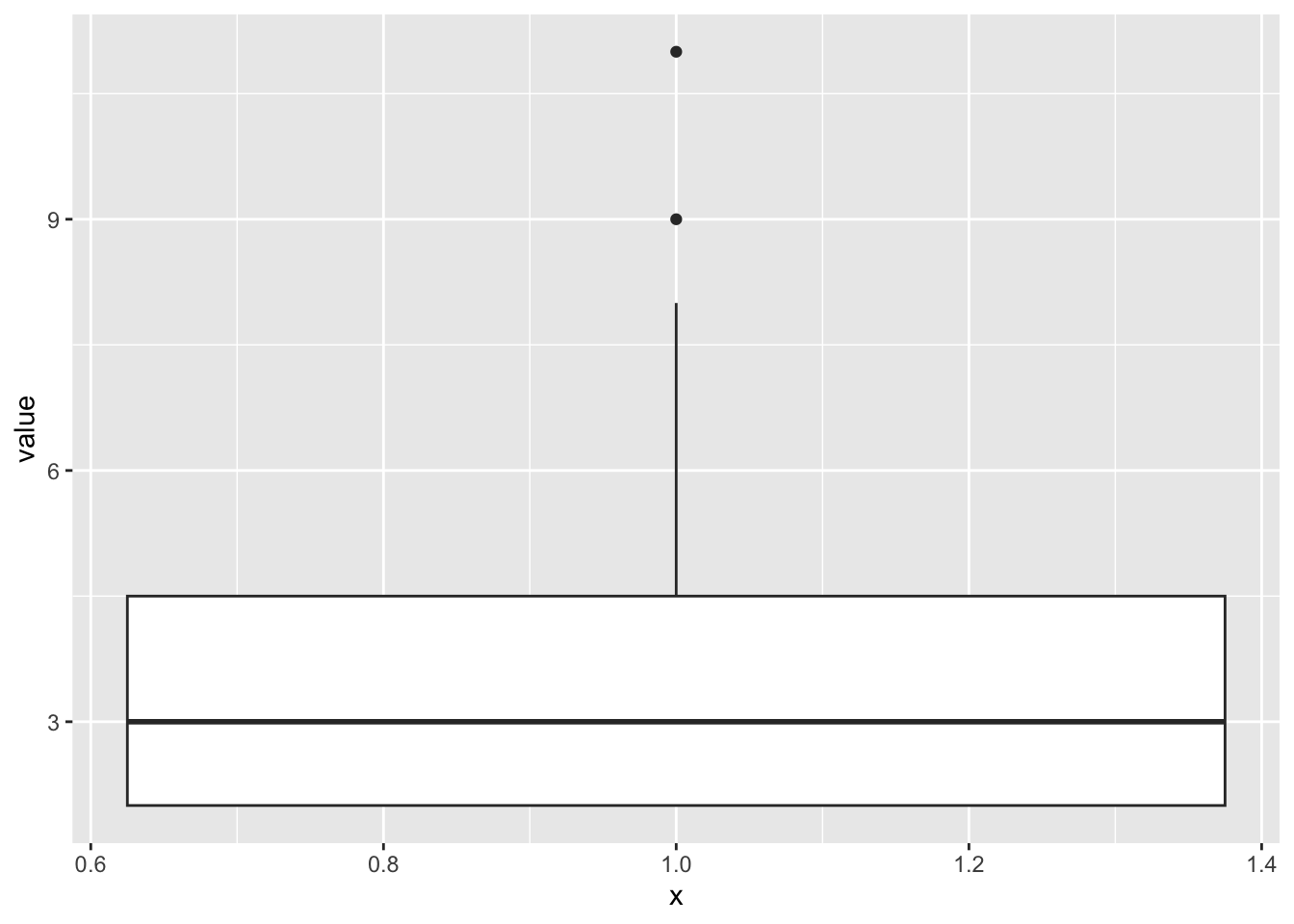
#names(dipodium)
library(conflicted)
library(janitor)
library(gt)
dipodium=clean_names(dipodium)
gt(head(dipodium))| tree_number | tree_species | dbh | plant_number | ramet_number | distance | orientation | number_of_flowers | height_inflo | herbivory | row_position_nf | number_flowers_position | number_of_fruits | perc_fr_set | pardalinum_or_roseum | fruit_position_effect | frutos_si_o_no | p_or_r_infl_lenght | num_of_fruits | species_name | cardinal_orientation |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | E.o | 75 | 1 | 1 | 2.47 | 40 | 11 | 35 | n | 1 | 24 | 0 | 0.00 | r | 1 | 0 | r | 0 | r | 1 |
| 1 | E.o | 76 | 2 | 1 | 1.97 | 50 | 19 | 47 | n | 2 | 23 | 0 | 0.00 | r | 2 | 0 | r | 0 | r | 2 |
| 2 | E.o | 76 | 3 | 1 | 1.95 | 350 | 18 | 63 | n | 3 | 25 | 1 | 0.04 | r | 3 | 0 | r | 1 | r | 8 |
| 3 | E.o | 58 | 4 | 1 | 3.24 | 210 | 24 | 47 | n | 4 | 20 | 5 | 0.25 | r | 4 | 0 | r | 5 | r | 5 |
| 4 | E.o | NA | 5 | 1 | 0.85 | 80 | 25 | 61 | n | 5 | 13 | 0 | 0.00 | r | 5 | 0 | r | 0 | r | 2 |
| 5 | E.o | 59 | 6 | 1 | 2.62 | 160 | 17 | 35 | n | 6 | 25 | 2 | 0.08 | p | 6 | 0 | r | 2 | p | 4 |
boxplot1 <- ggplot(d1, aes(number_of_fruits, x=1))+
geom_boxplot()+
annotate("text", x= .5,y= 5, label="Fig. 1")+
labs(x="", y="Cantidad de Frutos")+
theme(axis.title=element_text(size=10,face="bold"))boxplot2 <- ggplot(d1, aes(number_of_fruits, x=1))+
geom_boxplot(notch=TRUE) +
annotate("text", x= 0.7,y= 7, label="Fig. 2")+
labs(x="", y="Cantidad de Frutos")+
theme(axis.title=element_text(size=10,face="bold"))boxplot3 <- ggplot(d1, aes(number_of_fruits, x=1))+
geom_boxplot(notch=TRUE,colour="blue",
fill="orange", alpha=0.7, outlier.shape=18,
outlier.color="red", outlier.size=3)+
annotate("text", x= 0.7,y= 7, label="Fig. 3")+
labs(x="", y="Cantidad de Frutos")+
theme(axis.title=element_text(size=10,face="bold"))boxplot4 <- ggplot(d1, aes(factor(number_of_flowers), number_of_fruits))+
geom_boxplot(notch=FALSE)+
annotate("text", x= 2,y= 10, label="Fig. 4")+
labs(y="Cantidad de Frutos", x="Cantidad de Flores")+
theme(axis.title=element_text(size=10,face="bold"))+
theme(axis.text.x = element_text(angle = 90))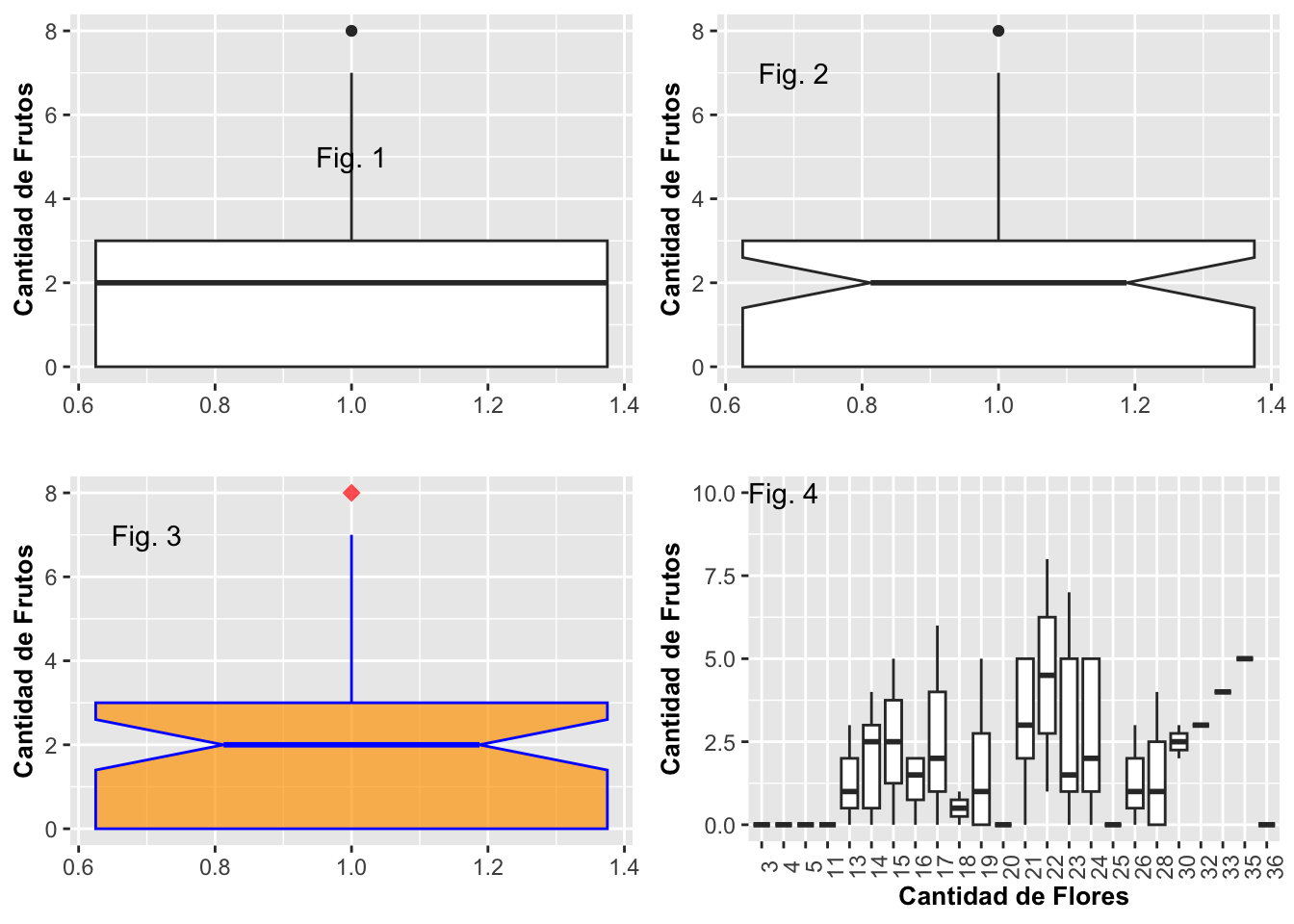
Cambiar el ancho de las cajas
Cambiar el ancho de las cajas con varwidth. Esto produce un diagrama de caja estándar y por defecto es FALSE; si es TRUE, produce un diagrama donde el ancho en el eje de X es proporcional a la raíz cuadrada del número de observaciones en los grupos.
\[x=\sqrt(n)\]
dipodium %>%
dplyr::select(number_of_flowers, number_of_fruits) %>%
drop_na() %>%
ggplot(aes(factor(number_of_flowers), number_of_fruits,
fill=factor(number_of_flowers)))+
geom_boxplot(varwidth=TRUE)+
theme(legend.position = "none")+
xlab("Cantidad de Flores")+
ylab("Cantidad de Frutos")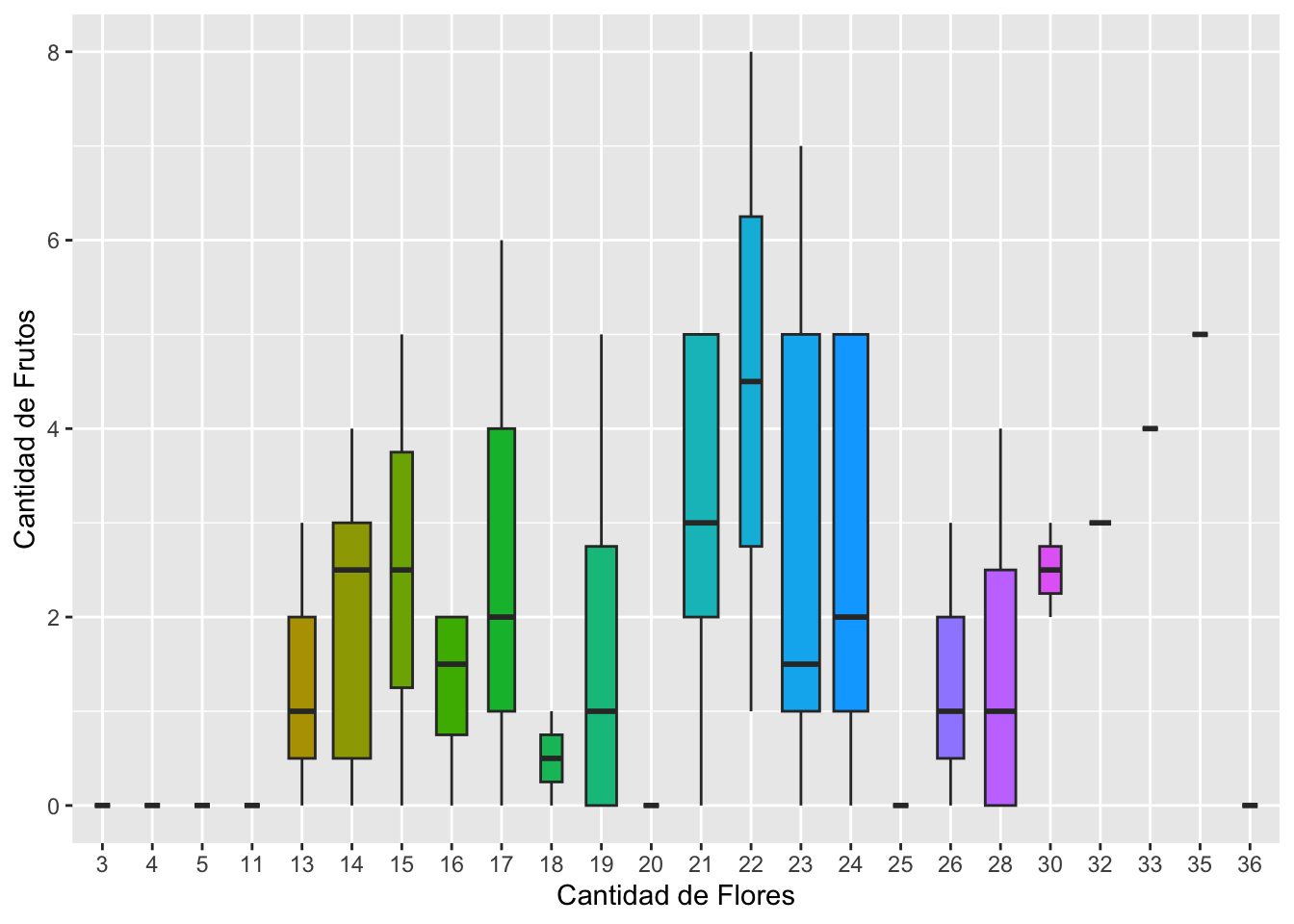
# la función varwidth =TRUE cambia
#el ancho de la barras basado en una formula indicado abajo.
# Más datos más ancho la barra. - Preparar un gráfico de caja (box plot) o tambien llamado Box
and whiskers. Utiliza los datos
ElphickBirdData en el paquete ggversa.
Utiliza la columna AQBIRDS, que son la cantidad de
pájaros acuaticos muestreados por Zuur, Ieno and Elphick. La especies de
pájaro de nombre Becasa de Mar =
Godwit es una ave migratoria que come pequeños moluscos
en la playas. Utiliza la columna “SITE” para crear un box plot con los
“notch”, por cada sitio de muestreo.
- Salvar el gráfico en formato .png y subirla a MSTeam.

La foto es de Leo Berzins via Flickr
Opciones y Parametros de geom_boxplot:
ggplot(el archivo de datos, aes(la variable continua, x=1)): {x=1} si es un grupo o el nombre de la variable discreta si hay múltiples grupos
geom_boxplot(stat, position, outlier.color, outlier.shape, outlier.size, notch, notchwidth, varwidth)
- stat: transformación estadística de los datos; solamente se necesita si se quiere anular el método por defecto que usa geom_boxplot
- position: para ajustar el solapamiento de los datos
- outlier.color: define el color de los valores atípicos
- outlier.shape: define la forma de los valores atípicos
- outlier.size: define el tamaño de los valores atípicos
- notch: para producir las muescas; se define con los valores TRUE o FALSE
- notchwidth: define el ancho de las muescas relativo a la caja (por defecto es 0.5)
- varwidth: produce un diagrama de caja estándar y por defecto es FALSE; si es TRUE, produce un diagrama donde el ancho en el eje de X es proporcional a la raíz cuadrada del número de observaciones en los grupos.